All Courses
Get the App Signup / Login
Sign in Open App
Class 9 Exam  >  Class 9 Notes  >  RD Sharma Solutions for Class 9 Mathematics  >  RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths

RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download

Question 1: Write the following in the expand form:

(i): (a+2b+c)2

(ii): (2a−3b−c)2

(iii): (−3x+y+z)2

(iv): (m+2n−5p)2

(v): (2+x−2y)2

(vi): (a2+b2+c2)2

(vii): (ab+bc+ca)2

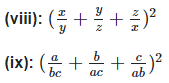
RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics

(x): (x+2y+4z)2

(xi): (2x−y+z)2

(xii): (−2x+3y+2z)2

Solution 1(i):

We have,

(a+2b+c)2 = a2+(2b)2+c2+2a(2b)+2ac+2(2b)c

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

?(a+2b+c)2 = a2+4b2+c2+4ab+2ac+4bc

Solution 1(ii):

We have,

(2a−3b−c)2 = [(2a)+(−3b)+(−c)]2

(2a)2+(−3b)2+(−c)2+2(2a)(−3b)+2(−3b)(−c)+2(2a)(−c)

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

4a2+9b2+c2−12ab+6bc−4ca

? (2a-3b-c)2 = 4x2+9y2+c2-12ab+6bc-4ca

Solution 1(iii):

We have,

(−3x+y+z)2 = [(−3x)2+y2+z2+2(−3x)y+2yz+2(−3x)z

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

9x2+y2+z2−6xy+2yz−6xz

(−3x+y+z)2 = 9x2+y2+z2−6xy+2xy−6xy

Solution 1(iv):

We have,

(m+2n−5p)2 = m2+(2n)2+(−5p)2+2m×2n+(2×2n×−5p)+2m×−5p

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

(m+2n−5p)2 = m2+4n2+25p2+4mn−20np−10pm

Solution 1(v):

We have,

(2+x−2y)2 = 22+x2+(−2y)2+2(2)(x)+2(x)(−2y)+2(2)(−2y)

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

= 4+x2+4y2+4x−4xy−8y

(2+x−2y)2 = 4+x2+4y2+4x−4xy−8y

Solution 1(vi):

We have,

(a2+b2+c2)2 = (a2)2+(b2)2+(c2)2+2a2b2+2b2c2+2a2c2

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

(a2+b2+c2)2 = a4+b4+c4+2a2b2+2b2c2+2c2a2

Solution 1(vii):

We have,

(ab+bc+ca)2 = (ab)2+(bc)2+(ca)2+2(ab)(bc)+2(bc)(ca)+2(ab)(ca)

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

= a2b2+b2c2+c2a2+2(ac)b2+2(ab)(c)2+2(bc)(a)2

(ab+bc+ca)2 = a2b2+b2c2+c2a2+2acb2+2abc2+2bca2

Solution 1(viii):

We have,

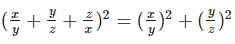
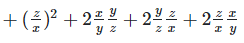
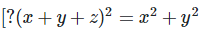
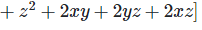
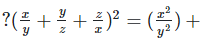
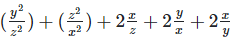
RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics
RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics
RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics

Solution 1(ix):

We have,

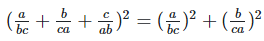
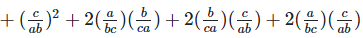
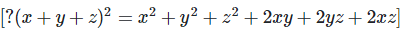
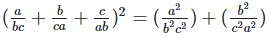
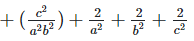
RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics
RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics
RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics

Solution 1(x):

We have,

We have,

(x+2y+4z)2 = x2+(2y)2+(4z)2+2x×2y+2×2y×4z+2x×4z

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

(x+2y+4z)2 = x2+4y2+16z2+4xy+16yz+8xz

Solution 1(xi):

We have,

(2x−y+z)2 = (2x)2+(−y)2+(z)2+2(2x)(−y)+2(−y)(z)+2(2x)(z)

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

(2x−y+z)2 = 4x2+y2+z2−4xy−2yz+4xz

Solution 1 (xii):

We have,

(−2x+3y+2z)2 = (−2x)2+(3y)2+(2z)2+2(−2x)(3y)+2(3y)(2z)+2(−2x)(2z)

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

(−4x+6y+4z)2 = 4x2+9y2+4z2−12xy+12yz−8xz

 

Question 2: Use algebraic identities to expand the following algebraic equations.

 Q 2.1: (a+b+c)2+(a−b+c)2

Ans : We have,

(a+b+c)2+(a−b+c)2 = (a2+b2+c2+2ab+2bc+2ca)+(a2+(−b)2+c2−2ab−2bc+2ca)

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

= 2a2+2b2+2c2+4ca

(a+b+c)2+(a−b+c)2 = 2a2+2b2+2c2+4ca

Q 2.2: (a+b+c)2−(a−b+c)2

Ans: We have,

(a+b+c)2−(a−b+c)2 = (a2+b2+c2+2ab+2bc+2ca)−(a2+(−b)2+c2−2ab−2bc+2ca)

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

= a2+b2+c2+2ab+2bc+2ca−a2−b2−c2+2ab+2bc−2ca)

= 4ab+4bc

(a+b+c)2−(a−b+c)2 = 4ab+4bc

Q 2.3: (a+b+c)2+(a+b−c)2+(a+b−c)2

Ans:  We have,

(a+b+c)2+(a+b−c)2+(a+b−c)2 = a2+b2+c2+2ab+2bc+2ca+(a2+b2+(z)2−2bc−2ab+2ca)+(a2+b2+c2−2ca−2bc+2ab)

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

= 3a2+3b2+3c2+2ab+2bc+2ca−2bc−2ab−2ca−2bc+2ab

= 3x2+3y2+3z2+2ab−2bc+2ca

(a+b+c)2+(a+b−c)2+(a−b+c)2 = 3a2+3b2+3c2+2ab−2bc+2ca

(a+b+c)2+(a+b−c)2+(a−b+c)2 = 3(a2+b2+c2)+2(ab−bc+ca)

Q 2.4: (2x+p−c)2−(2x−p+c)2

Ans: We have,

(2x+p−c)2−(2x−p+c)2 = [2x2+p2+(−c)2+2(2x)p+2p(−c)+2(2x)(−c)]−[4x2+(−p)2+c2+2(2x)(−p)+2c(−p)+2(2x)c]

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

(2x+p−c)2−(2x−p+c)2 = [4x2+p2+c2+4xp−2pc−4xc]−[4x2+p2+c2−4xp−2pc+4xc]

Opening the bracket,

(2x+p−c)2−(2x−p+c)2 = 4x2+p2+c2+4xp−2pc−4cx−4x2−p2−c2+4xp+2pc−4cx]

(2x+p−c)2−(2x−p+c)2 = 8xp−8xc

= 8x(p−c)

Hence, (2x+p−c)2−(2x−p+c)2 = 8x(p−c)

Q 2.5: (x2+y2+(−z)2)−(x2−y2+z2)2

Ans: We have,

(x2+y2+(−z)2)2−(x2(−y)2+z2)2

=[x4+y4+(−z)4+2x2y2+2y2(−z)2+2x2(−z)2]−[x4+(−y)4+z4−2x2y2−2y2z22+2x2z2]

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

Taking the negative sign inside,

= [x4+y4+(−z)4+2x2y2+2y2(−z)2+2x2(−z)2]−[x4+(−y)4+z4−2x2y2−2y2z2+2x2z2]

= 4x2y2–4z2x2

Hence, (x2+y2+(−z)2)2−(x2(−y)2+z2)2 = 4x2y2–4z2x2


Q3: If a+b+c = 0 and a2+b2+c2 = 16, find the value of ab+bc+ca:

Ans:  We know that,

[?(a+b+c)2 = a2+b2+c2+2ab+2bc+2ca]

(0)2 = 16+2(ab+bc+ca)

2(ab+bc+ca) = -16

ab+bc+ca = -8

Hence, value of required express ab+bc+ca =-8


Q4: If a2+b2+c2 = 16 and ab+bc+ca = 10, find the value of a+b+c?

Ans: We know that,

(a+b+c)2 = a2+b2+c2+2(ab+bc+ca)

(x+y+z)2 = 16+2(10)

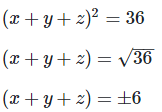
RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics

Hence, value of required expression I; (a+b+c)=±8

Q5: If a+b+c = 9 and ab+bc+ca = 23, find value of a2+b2+c2

Ans: We know that,

(a+b+c)2 = a2+b2+c2+2(ab+bc+ca)

92 = a2+b2+c2+2(23)

81 = a2+b2+c2+46

a2+b2+c2 = 81−46

a2+b2+c2 = 35

Hence, value of required expression a2+b2+c2 = 35


Q6: Find the value of the equation : 4x2+y2+25z2+4xy−10yz−20zx when x = 4,y = 3,z = 2

Ans: 4x2+y2+25z2+4xy−10yz−20zx

(2x)2+y2+(−5z)2+2(2x)(y)+2(y)(−5z)+2(−5z)(2x)

(2x+y−5z)2

(2(4)+3−5(2))2

(8+3−10)2

(1)2

1

Hence value of the equation is equals to 1


Q7: Simplify each of the following expressions:

Q 7.1: 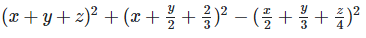RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics

Ans: Expanding, we get

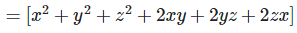
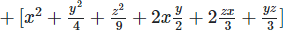
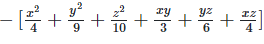
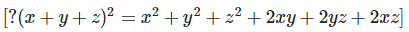
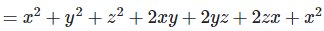
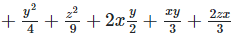
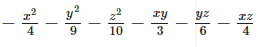
RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics

RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics

Rearranging coefficients ,

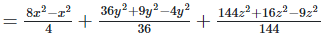
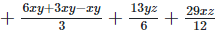
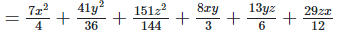
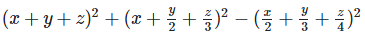
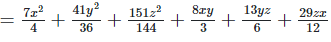
RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics

RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics

RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics

Q 7.2: (x+y−2z)2−x2−y2−3z2+4xy

Ans:  (x+y−2z)2−x2−y2−3z2+4xy

= [x2+y2+4z2+2xy+2y(−2z)+2a(−2c)]−x2−y2−3z2+4xy

= z2+6xy−4yz−4zx

(x+y−2z)2−x2−y2−3z2+4xy = z2+6xy−4yz−4zx


Q 7.3: [x2−x+1]2−[x2+x+1]2

Ans:  [x2−x+1]2−[x2+x+1]2

=(x2)2+(−x)2+12+2(x2)(−x)+2(−x)(1)+2x2)−[(x2)2+x2+1+2x2x+2x(1)+2x2(1)]

[?(x+y+z)2 = x2+y2+z2+2xy+2yz+2xz]

= x4+y2+1−2x3−2x+2x2−x2−x4−1−2x3−2x−2x2

= −4x3−4x

= −4x(x2+1)

Hence simplified equation = [x2−x+1]2−[x2+x+1]2 = −4x(x2+1)

The document RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics is a part of the Class 9 Course RD Sharma Solutions for Class 9 Mathematics.
All you need of Class 9 at this link: Class 9
91 docs
Join Course for Free

Top Courses for Class 9

FAQs on RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics

1. What are algebraic identities?
Ans. Algebraic identities are mathematical expressions that remain true for any values of the variables involved. They are used to simplify and solve algebraic equations.
2. What are some common algebraic identities used in Class 9 Maths?
Ans. Some common algebraic identities used in Class 9 Maths are: - (a + b)^2 = a^2 + 2ab + b^2 - (a - b)^2 = a^2 - 2ab + b^2 - a^2 - b^2 = (a + b)(a - b) - (a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2ac + 2bc - (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3
3. How can algebraic identities be used to simplify expressions?
Ans. Algebraic identities can be used to simplify expressions by replacing complex expressions with simpler ones. By applying the appropriate identity, we can expand or factorize expressions, making them easier to manipulate and solve.
4. Are algebraic identities only applicable in algebra?
Ans. No, algebraic identities are not only applicable in algebra. They have applications in various mathematical fields, such as geometry, calculus, and number theory. They are used to simplify equations, prove theorems, and solve problems in these areas.
5. Can algebraic identities be used to solve real-life problems?
Ans. Yes, algebraic identities can be used to solve real-life problems. They provide a framework for representing and manipulating mathematical relationships, which can be applied to various real-world scenarios. For example, they can be used to solve problems in physics, economics, and engineering by modeling the relationships between variables and finding solutions analytically.
Related Exams
About this Document
4.86/5 Rating
Dec 23, 2024 Last updated
Document Description: RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths for Class 9 2024 is part of RD Sharma Solutions for Class 9 Mathematics preparation. The notes and questions for RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths have been prepared according to the Class 9 exam syllabus. Information about RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths covers topics like and RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths Example, for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths.
Introduction of RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths in English is available as part of our RD Sharma Solutions for Class 9 Mathematics for Class 9 & RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths in Hindi for RD Sharma Solutions for Class 9 Mathematics course. Download more important topics related with notes, lectures and mock test series for Class 9 Exam by signing up for free. Class 9: RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics
Description
Full syllabus notes, lecture & questions for RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics - Class 9 | Plus excerises question with solution to help you revise complete syllabus for RD Sharma Solutions for Class 9 Mathematics | Best notes, free PDF download
Information about RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths
In this doc you can find the meaning of RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths defined & explained in the simplest way possible. Besides explaining types of RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths tests, examples and also practice Class 9 tests
Explore Courses for Class 9 exam

Top Courses for Class 9

Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Related Searches

MCQs

,

past year papers

,

RD Sharma Solutions Ex-4.2

,

Semester Notes

,

RD Sharma Solutions Ex-4.2

,

Free

,

Summary

,

pdf

,

Maths | RD Sharma Solutions for Class 9 Mathematics

,

Exam

,

Objective type Questions

,

practice quizzes

,

Maths | RD Sharma Solutions for Class 9 Mathematics

,

Important questions

,

Previous Year Questions with Solutions

,

video lectures

,

Class 9

,

Sample Paper

,

ppt

,

study material

,

shortcuts and tricks

,

Algebraic Identities

,

mock tests for examination

,

RD Sharma Solutions Ex-4.2

,

Maths | RD Sharma Solutions for Class 9 Mathematics

,

Extra Questions

,

Algebraic Identities

,

Class 9

,

Class 9

,

Viva Questions

,

Algebraic Identities

;
Additional Information about RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths for Class 9 Preparation

RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths Free PDF Download

The RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths is an invaluable resource that delves deep into the core of the Class 9 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths now and kickstart your journey towards success in the Class 9 exam.

Importance of RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths

The importance of RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths cannot be overstated, especially for Class 9 aspirants. This document holds the key to success in the Class 9 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths Notes

RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths Notes on EduRev are your ultimate resource for success.

RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths Class 9 Questions

The "RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths on the App

Students of Class 9 can study RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of RD Sharma Solutions Ex-4.2, Algebraic Identities, Class 9, Maths is prepared as per the latest Class 9 syllabus.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup