Ex-5.1, (Part - 2) Factorization Of Algebraic Expressions, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q20 . x2−y2−4xz+4z2
SOLUTION :
On rearranging the terms
= x2−4xz+4z2−y2
= (x)2−2×x×2z+(2z)2−y2
Using the identity x2−2xy+y2=(x−y)2
= (x−2z)2−y2
Using the identity p2−q2= ( p + q )( p – q )
= (x−2z+y)(x−2z−y)
∴ x2−y2−4xz+4z2 = (x−2z+y)(x−2z−y)
Q21 .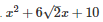
SOLUTION :
Splitting the middle term ,
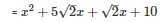
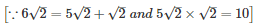
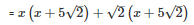
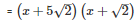
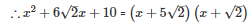
Q22 . 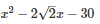
SOLUTION :
Splitting the middle term,
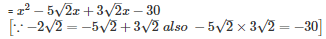
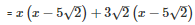
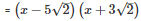
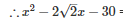 =
=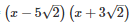
Q23 . 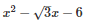
SOLUTION :
Splitting the middle term,
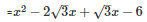
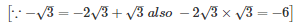
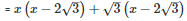
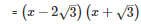
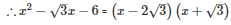
Q24 . 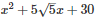
SOLUTION :
Splitting the middle term,
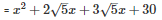
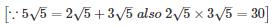
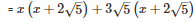
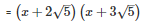
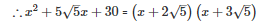
Q25 .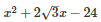
SOLUTION :
Splitting the middle term,
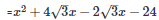
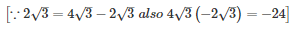
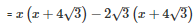
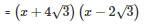

Q26 . 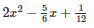
SOLUTION :
Splitting the middle term,
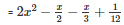
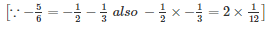
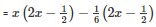
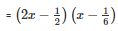
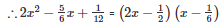
Q27 . 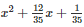
SOLUTION :
Splitting the middle term,
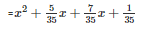
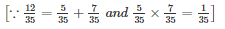
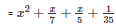
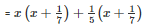
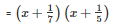
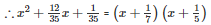
Q28 .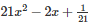
SOLUTION :
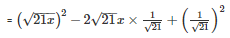
Using the identity (x−y)2=x2+y2−2xy
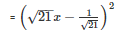
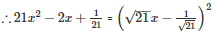
Q29 . 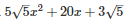
SOLUTION :
Splitting the middle term,
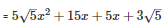
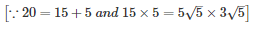
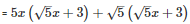
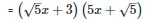
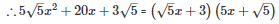
Q30 .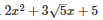
SOLUTION :
Splitting the middle term,
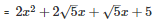
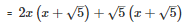
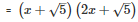
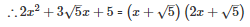
Q31 . 9(2a−b)2−4(2a−b)−13
SOLUTION :
Let 2a – b = x
= 9x2−4x−13
Splitting the middle term,
= 9x2−13x+9x−13
= x(9x−13)+1(9x−13)
= (9x−13)(x+1)
Substituting x = 2a – b
= [9(2a−b)−13](2a−b+1)
= (18a−9b−13)(2a−b+1)
∴ 9(2a−b)2−4(2a−b)−13 = (18a−9b−13)(2a−b+1)
Q 32 . 7(x−2y)2−25(x−2y)+12
SOLUTION :
Let x-2y = P
= 7P2−25P+12
Splitting the middle term,
= 7P2−21P−4P+12
= 7P(P−3)−4(P−3)
= (P−3)(7P−4)
Substituting P = x – 2y
= (x−2y−3)(7(x−2y)−4)
= (x−2y−3)(7x−14y−4)
∴ 7(x−2y)2−25(x−2y)+12 = (x−2y−3)(7x−14y−4)
Q33 . 2(x+y)2−9(x+y)−5
SOLUTION :
Let x+y = z
= 2z2−9z−5
Splitting the middle term,
= 2z2−10z+z−5
= 2z(z−5)+1(z−5)
= (z−5)(2z+1)
Substituting z = x + y
= (x+y−5)(2(x+y)+1)
= (x+y−5)(2x+2y+1)
∴ 2(x+y)2−9(x+y)−5 = (x+y−5)(2x+2y+1)
Q34 . Give the possible expression for the length & breadth of the rectangle having 35y2−13y−12 as its area.
SOLUTION :
Area is given as 35y2−13y−12
Splitting the middle term,
Area = 35y2+218y−15y−12
= 7y(5y+4)−3(5y+4)
= (5y+4)(7y−3)
We also know that area of rectangle = length ×breadth
∴ Possible length = (5y+4) and breadth=(7y−3)
Or possible length = (7y−3) and breadth= (5y+4)
Q35 . What are the possible expression for the cuboid having volume 3x2−12x.
SOLUTION :
Volume = 3x2−12x
= 3x(x−4)
= 3×x(x−4)
Also volume = Length ×Breadth×Height
∴ Possible expression for dimensions of cuboid are = 3 , x , (x−4)
FAQs on Ex-5.1, (Part - 2) Factorization Of Algebraic Expressions, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is factorization of algebraic expressions? |  |
| 2. Why is factorization important in algebra? |  |
| 3. How do you factorize an algebraic expression? |  |
| 4. What are the benefits of learning factorization of algebraic expressions? |  |
| 5. Can you provide an example of factorization of an algebraic expression? |  |
















