RD Sharma Solutions Ex-6.1, Factorization Of Polynomials, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1. Which of the following expressions are polynomials in one variable and which are not?
1. 3x2–4x+15
2. y2+2√3
3. 3√x+√2x
4. 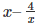
5. x12+y2+t50
Sol :
1. 3x2–4x+15 – it is a polynomial of x
2. y2+2√3 – it is a polynomial of y
3. 3√x+√2x – it is not a polynomial since the exponent of 3√x is not a positive term
4. 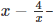 it is not a polynomial since the exponent of
it is not a polynomial since the exponent of 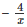 is not a positive term
is not a positive term
5. x12+y2+t50 – it is a three variable polynomial which variables of x, y, t
Q2. Write the coefficients of x2 in each of the following
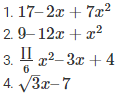
Sol :
Given , to find the coefficients of x2
1. 17–2x+7x2 – the coefficient is 7
2. 9–12x+x2 – the coefficient is 0
3. 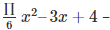 the coefficient is
the coefficient is 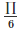
4. 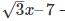 the coefficient is 0
the coefficient is 0
Q3. Write the degrees of each of the following polynomials :
1. 7x3+4x2–3x+12
2. 12–x+2x2
3. 5y–√2
4. 7−7x0
5. 0
Sol :
Given , to find degrees of the polynomials
Degree is highest power in the polynomial
1. 7x3+4x2–3x+12 – the degree is 3
2. 12–x+2x3 – the degree is 3
3. 5y–√2 – the degree is 1
4. 7−7x0 – the degree is 0
5. 0 – the degree of 0 is not defined
Q4. Classify the following polynomials as linear, quadratic, cuboc and biquadratic polynomials :
1. x+x2+4
2. 3x – 2
3. 2x+x2
4. 3y
5. t2+1
f . 7t4+4t2+3t–2
Sol :
Given
1. x+x2+4 – it is a quadratic polynomial as its degree is 2
2. 3x – 2 – it is a linear polynomial as its degree is 1
3. 2x+x2 – it is a quadratic polynomial as its degree is 2
4. 3y – it is a linear polynomial as its degree is 1
5. t2+1 – it is a quadratic polynomial as its degree is 2
f . 7t4+4t2+3t–2 – it is a bi- quadratic polynomial as its degree is 4
Q5. Classify the following polynomials as polynomials in one variables, two – variables etc :
1. x2–xy+7y2
2. x2–2tx+7t2–x+t
3. t3–3t2+4t–5
4. xy + yz + zx
Sol :
Given
1. x2–xy+7y2 – it is a polynomial in two variables x and y
2. x2–2tx+7t2–x+t – it is a polynomial in two variables x and t
3. t3–3t2+4t–5– it is a polynomial in one variable t
4. xy+yz+zx – it is a polynomial in 3 variables in x , y and z
Q6. Identify the polynomials in the following :
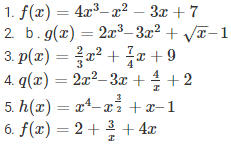
Sol :
Given
1. f(x) = 4x3–x2−3x+7 – it is a polynomial
2. b. g(x) = 2x3–3x2+√x–1 – it is not a polynomial since the exponent of √x is a negative integer
3. 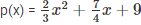 it is a polynomial as it has positive integers as exponents
it is a polynomial as it has positive integers as exponents
4. 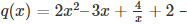 it is not a polynomial since the exponent of 4/x is a negative integer
it is not a polynomial since the exponent of 4/x is a negative integer
5. 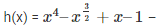 it is not a polynomial since the exponent of
it is not a polynomial since the exponent of 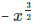 is a negative integer
is a negative integer
6. 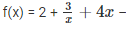 it is not a polynomial since the exponent of 3/x is a negative integer
it is not a polynomial since the exponent of 3/x is a negative integer
Q7. Identify constant , linear , quadratic abd cubic polynomial from the following polynomials :
1. f(x) = 0
2. g(x) = 2x3–7x+4
3. 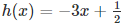
4. p(x) = 2x2–x+4
5. q(x) = 4x+3
6. r(x) = 3x3+4x2+5x–7
Sol :
Given ,
1. f(x) = 0 – as 0 is constant , it is a constant variable
2. g(x) = 2x3–7x+4 – since the degree is 3 , it is a cubic polynomial
3. 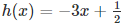 – since the degree is 1 , it is a linear polynomial
– since the degree is 1 , it is a linear polynomial
4. p(x) = 2x2–x+4 – since the degree is 2 , it is a quadratic polynomial
5. q(x) = 4x+3 – since the degree is 1 , it is a linear polynomial
6. r(x) = 3x3+4x2+5x–7 – since the degree is 3 , it is a cubic polynomial
Q8. Give one example each of a binomial of degree 25, and of a monomial of degree 100
Sol :
Given , to write the examples for binomial and monomial with the given degrees
Example of a binomial with degree 25 – 7x35–5
Example of a monomial with degree 100 – 2t100
FAQs on RD Sharma Solutions Ex-6.1, Factorization Of Polynomials, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. How do I factorize a polynomial? |  |
| 2. Can all polynomials be factorized? |  |
| 3. Is there a general formula for factorizing polynomials? |  |
| 4. What is the importance of factorizing polynomials? |  |
| 5. Can factorization of polynomials be used in real-life situations? |  |
















