RD Sharma Solutions Ex-6.2, Factorization Of Polynomials, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1. If f(x) = 2x3–13x2+17x+12 , Find
1. f(2)
2. f(-3)
3. f(0)
Sol :
The given polynomial is f(x) = 2x3–13x2+17x+12
1. f(2)
we need to substitute the ‘2‘ in f(x)
f(2) = 2(2)3–13(2)2+17(2)+12
= (2 * 8) – (13 * 4) + (17 * 2) + 12
= 16 – 52 + 34 + 12
= 10
therefore f(2) = 10
2. f(-3)
we need to substitute the ‘ (-3) ‘ in f(x)
f(-3) =2(−3)3–13(−3)2+17(−3)+12
= (2 * -27) – ( 13 * 9) – ( 17 * 3) + 12
= -54 – 117 – 51 + 12
= -210
therefore f(-3) = -210
3. f(0)
we need to substitute the ‘(0)‘ in f(x)
f(0) = 2(0)3–13(0)2+17(0)+12
= ( 2 * 0) – ( 13 * 0) + (17 * 0) + 12
= 0 – 0 + 0 + 12
= 12
therefore f(0) = 12
Q2. Verify whether the indicated numbers are zeros of the polynomial corresponding to them in the following cases :
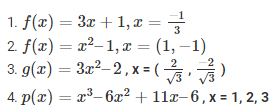
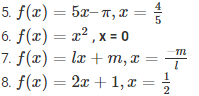
Sol :
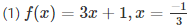
we know that ,
f(x) = 3x + 1
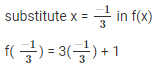
= -1 + 1
= 0
Since, the result is 0 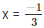 is the root of 3x + 1
is the root of 3x + 1
(2) f(x) = x2–1,x = (1,−1)
we know that,
f(x) = x2 – 1
Given that x = (1 , -1)
substitute x = 1 in f(x)
f(1) = 12 – 1
= 1 – 1
= 0
Now , substitute x = (-1) in f(x)
f(-1) = (−1)2 – 1
= 1 – 1
= 0
Since , the results when x = (1 , -1) are 0 they are the roots of the polynomial f(x) = x2 – 1
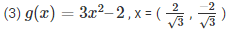
Sol :
We know that
g(x) = 3x2–2
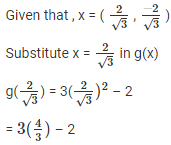
= 4 – 2
= 2 ≠ 0
Now, Substitute 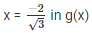
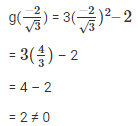
Since, the results when 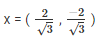 are not 0, they are roots of 3x2–2
are not 0, they are roots of 3x2–2
(4) p(x) = x3–6x2+11x–6 , x = 1, 2, 3
Sol :
We know that ,
p(x) = x3–6x2+11x–6
given that the values of x are 1, 2 , 3
substitute x = 1 in p(x)
p(1) = 13–6(1)2+11(1)–6
= 1 – (6 * 1) + 11 – 6
= 1 – 6 + 11 – 6
= 0
Now, substitute x = 2 in p(x)
P(2) =23–6(2)2+11(2)–6
= (2 * 3) – ( 6 * 4) + ( 11 * 2) – 6
= 8 – 24 – 22 – 6
= 0
Now, substitute x = 3 in p(x)
P(3) = 33–6(3)2+11(3)–6
= ( 3 * 3) – (6 * 9) + (11 * 3) – 6
= 27 – 54 + 33 – 6
= 0
Since , the result is 0 for x = 1, 2, 3 these are the roots of x3–6x2+11x–6
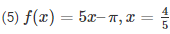
we know that ,
f(x) = 5x–π
Given that , x = 4/5
Substitute the value of x in f(x)
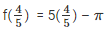
= 4 – π
≠ 0
Since , the result is not equal to zero , x = 4/5 is not the root of the polynomial 5x – π
(6) f(x) = x2 , x = 0
Sol :
we know that , f(x) = x2
Given that value of x is ‘ 0 ’
Substitute the value of x in f(x)
f(0) = 02
= 0
Since, the result is zero , x = 0 is the root of x2
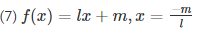
Sol :
We know that,
f(x) = lx + m
Given , that 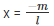
Substitute the value of x in f(x)
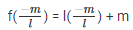
= -m + m
= 0 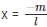 is the root of lx + m
is the root of lx + m
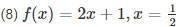
Sol :
We know that ,
f(x) = 2x + 1
Given that x = 1/2
Substitute the value of x and f(x)
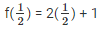
= 1 + 1
= 2 ≠ 0
Since , the result is not equal to zero
x = 1/2 is the root of 2x + 1
Q3. If x = 2 is a root of the polynomial f(x) = 2x2–3x+7a, Find the value of a
Sol :
We know that , f(x) = 2x2–3x+7a
Given that x = 2 is the root of f(x)
Substitute the value of x in f(x)
f(2) = 2(2)2–3(2)+7a
= (2 * 4) – 6 + 7a
= 8 – 6 + 7a
= 7a + 2
Now, equate 7a + 2 to zero
⇒ 7a + 2 = 0
⇒ 7a = -2
⇒ 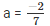
The value of 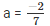
Q4. If 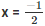 is zero of the polynomial p(x) = 8x3–ax2–x+2 , Find the value of a
is zero of the polynomial p(x) = 8x3–ax2–x+2 , Find the value of a
Sol :
We know that , p(x) = 8x3–ax2–x+2
Given that the value of 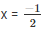
Substitute the value of x in f(x)
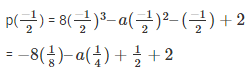
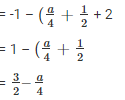
To , find the value of a , equate 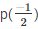 to zero
to zero
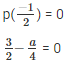
On taking L.C.M
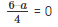
⇒ 6 – a = 0
⇒ a = 6
Q5. If x = 0 and x = -1 are the roots of the polynomial f(x) = 2x3–3x2+ax+b , Find the of a and b.
Sol :
We know that , f(x) = 2x3–3x2+ax+b
Given , the values of x are 0 and -1
Substitute x = 0 in f(x)
f(0) = 2(0)3–3(0)2+a(0)+b
= 0 – 0 + 0 + b
= b ——— 1
Substitute x = (-1) in f(x)
f(-1) = 2(−1)3–3(−1)2+a(−1)+b
= -2 – 3 – a + b
= -5 – a + b ———— 2
We need to equate equations 1 and 2 to zero
b = 0 and -5 – a + b = 0
since, the value of b is zero
substitute b = 0 in equation 2
⇒ -5 – a = -b
⇒ -5 – a = 0
a = -5
the values of a and b are -5 and 0 respectively
Q6. Find the integral roots of the polynomial f(x) = x3+6x2+11x+6
Sol :
Given , that f(x) = x3+6x2+11x+6
Clearly we can say that, the polynomial f(x) with an integer coefficient and the highest degree term coefficient which is known as leading factor is 1.
So, the roots of f(x) are limited to integer factor of 6, they are
±1, ±2, ±3, ±6
Let x = -1
f(-1) = (−1)3+6(−1)2+11(−1)+6
= -1 + 6 -11 + 6
= 0
Let x = -2
f(-2) = (−2)3+6(−2)2+11(−2)+6
= -8 – (6 * 4) – 22 + 6
= -8 + 24 – 22 + 6
= 0
Let x = -3
f(-3) = (−3)3+6(−3)2+11(−3)+6
= -27 – (6 * 9) – 33 + 6
= -27 + 54 – 33 + 6
= 0
But from all the given factors only -1 , -2 , -3 gives the result as zero .
So, the integral multiples of x3+6x2+11x+6 are -1 , -2 , -3
Q7. Find the rational roots of the polynomial f(x) = 2x3+x2–7x–6
Sol :
Given that f(x) = 2x3+x2–7x–6
f(x) is a cubic polynomial with an integer coefficient . If the rational root in the form of p/q , the values of p are limited to factors of 6 which are ±1, ±2, ±3, ±6
and the values of q are limited to the highest degree coefficient i.e 2 which are ±1, ±2
here, the possible rational roots are
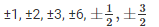
Let , x = -1
f(-1) = 2(−1)3+(−1)2–7(−1)–6
= -2 + 1 +7 – 6
= -8 + 8
= 0
Let , x = 2
f(-2) = 2(2)3+(2)2–7(2)–6
= ( 2 * 8) + 4 -14 – 6
= 16 + 4 -14 – 6
= 20 – 20
= 0
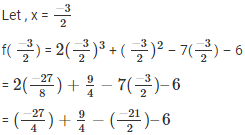
But from all the factors only -1 , 2 and −3/2 gives the result as zero
So, the rational roots of 2x3+x2–7x–6 are -1, 2 and −3/2
FAQs on RD Sharma Solutions Ex-6.2, Factorization Of Polynomials, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is factorization of polynomials? |  |
| 2. How do you factorize a polynomial? |  |
| 3. What are the benefits of factorizing polynomials? |  |
| 4. Can all polynomials be factorized? |  |
| 5. How is factorization of polynomials useful in real-life applications? |  |
















