RD Sharma Solutions Ex-6.3, Factorization Of Polynomials, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
In each of the following , using the remainder theorem, find the remainder when f(x) is divided by g(x) and verify the by actual division : (1 – 8)
Q1. f(x) = x3+4x2–3x+10 , g(x) = x + 4
Sol :
Here, f(x) = x3+4x2–3x+10
g(x) = x + 4
from, the remainder theorem when f(x) is divided by g(x) = x – (-4) the remainder will be equal to f(-4)
Let , g(x) = 0
⇒ x + 4 = 0
⇒ x = -4
Substitute the value of x in f(x)
f(-4) = (−4)3+4(−4)2–3(−4)+10
= -64 + ( 4 * 16) + 12 + 10
= -64 + 64 + 12 + 10
= 12 + 10
= 22
Therefore, the remainder is 22
Q2. f(x) = 4x4–3x3–2x2+x–7 , g(x) = x – 1
Sol :
Here, f(x) = 4x4–3x3–2x2+x–7
g(x) = x – 1
from, the remainder theorem when f(x) is divided by g(x) = x – (-1) the remainder will be equal to f(1)
Let , g(x) = 0
⇒ x – 1 = 0
⇒ x = 1
Substitute the value of x in f(x)
f(1) = 4(1)4–3(1)3–2(1)2+1–7
= 4 – 3 – 2 + 1 – 7
= 5 – 12
= -7
Therefore, the remainder is 7
Q3. f(x) = 2x4–6x3+2x2–x+2 , g(x) = x + 2
Sol :
Here, f(x) = 2x4–6x3+2x2–x+2
g(x) = x + 2
from, the remainder theorem when f(x) is divided by g(x) = x – (-2) the remainder will be equal to f(-2)
Let , g(x) = 0
⇒ x + 2 = 0
⇒ x = -2
Substitute the value of x in f(x)
f(-2) = 2(−2)4–6(−2)3+2(−2)2–(−2)+2
= (2 * 16) – (6 * (-8)) + (2 * 4) + 2 + 2
= 32 + 48 + 8 + 2 + 2
= 92
Therefore, the remainder is 92
Q4. f(x) = 4x3–12x2+14x–3 , g(x) = 2x – 1
Sol:
Here, f(x) = 4x3–12x2+14x–3
g(x) = 2x – 1
from, the remainder theorem when f(x) is divided by g(x) =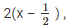 the remainder is equal to f(1/2)
the remainder is equal to f(1/2)
Let , g(x) = 0
⇒ 2x – 1 = 0
⇒ 2x = 1
⇒ x = 1/2
Substitute the value of x in f(x)
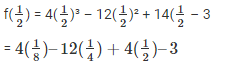
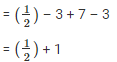
Taking L.C.M

Therefore, the remainder is 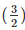
Q5. f(x) = x3–6x2+2x–4 , g(x) = 1 – 2x
Sol :
Here, f(x) = x3–6x2+2x–4
g(x) = 1 – 2x
from, the remainder theorem when f(x) is divided by g(x) = -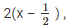 the remainder is equal to f(1/2)
the remainder is equal to f(1/2)
Let , g(x) = 0
⇒ 1 – 2x = 0
⇒ -2x = -1
⇒ 2x = 1
⇒ x = 1/2
Substitute the value of x in f(x)
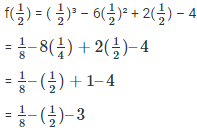
Taking L.C.M
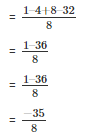
Therefore, the remainder is 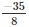
Q6. f(x) = x4–3x2+4 , g(x) = x – 2
Sol :
Here, f(x) = x4–3x2+4
g(x) = x – 2
from, the remainder theorem when f(x) is divided by g(x) = x – 2 the remainder will be equal to f(2)
let , g(x) = 0
⇒ x – 2 = 0
⇒ x = 2
Substitute the value of x in f(x)
f(2) = 24–3(2)2+4
= 16 – (3* 4) + 4
= 16 – 12 + 4
= 20 – 12
= 8
Therefore, the remainder is 8
Q7. f(x) = 9x3–3x2+x–5 , g(x) 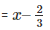
Sol :
Here, f(x) = 9x3–3x2+x–5
g(x) = 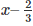
from, the remainder theorem when f(x) is divided by g(x) = 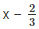 the remainder will be equal to f(1/2) substitute the value of x in f(x)
the remainder will be equal to f(1/2) substitute the value of x in f(x)
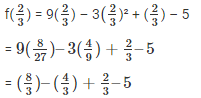
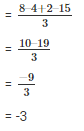
Therefore, the remainder is -3
Q8. 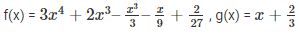
Sol :
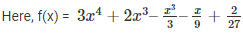

from remainder theorem when f(x) is divided by g(x) 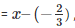 the remainder is equal to
the remainder is equal to 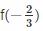 substitute the value of x in f(x)
substitute the value of x in f(x)
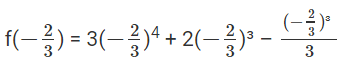
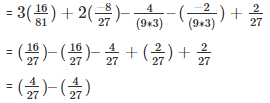
= 0
Therefore, the remainder is 0
Q9. If the polynomial 2x3+ax2+3x–5 and x3+x2–4x+a leave the same remainder when divided by x – 2 , Find the value of a
Sol :
Given , the polymials are
f(x) = 2x3+ax2+3x–5
p(x) = x3+x2–4x+a
The remainders are f(2) and p(2) when f(x) and p(x) are divided by x – 2
We know that,
f(2) = p(2) (given in problem)
we need to calculate f(2) and p(2)
for, f(2)
substitute (x = 2) in f(x)
f(2) = 2(2)3+a(2)2+3(2)–5
= (2 * 8) + a4 + 6 – 5
= 16 + 4a + 1
= 4a + 17 ——- 1
for, p(2)
substitute (x = 2) in p(x)
p(2) = 23+22–4(2)+a
= 8 + 4 – 8 + a
= 4 + a ——— 2
Since, f(2) = p(2)
Equate eqn 1 and 2
⇒ 4a + 17 = 4 + a
⇒ 4a – a = 4 – 17
⇒ 3a = -13
⇒ 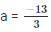
Q10. If polynomials ax3+3x2–3 and 2x3–5x+a when divided by (x – 4) leave the remainders as R1 and R2 respectively. Find the values of a in each of the following cases, if
1. R1 = R2
2. R1+R2 = 0
3. 2R1–R2 = 0
Sol :
Here, the polynomials are
f(x) = ax3+3x2–3
p(x) = 2x3–5x+a
let,
R1 is the remainder when f(x) is divided by x – 4
⇒ R1 = f(4)
⇒ R1 = a(4)3+3(4)2–3
= 64a + 48 – 3
= 64a + 45 ——— 1
Now , let
R2 is the remainder when p(x) is divided by x – 4
⇒ R2 = p(4)
⇒ R2 = 2(4)3–5(4)+a
= 128 – 20 + a
= 108 + a ——– 2
1. Given , R1 = R2
⇒ 64a + 45 = 108 + a
⇒ 63a = 63
⇒ a = 1
2. Given, R1+R2 = 0
⇒ 64a + 45 + 108 + a = 0
⇒ 65a + 153 = 0
⇒ 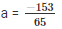
3.Given, 2R1–R2 = 0
⇒ 2(64a + 45) – 108 – a = 0
⇒ 128a + 90 – 108 – a = 0
⇒ 127a – 18 = 0
⇒ a = 18/127
Q11. If the polynomials ax3+3x2–13 and 2x3–5x+a when divided by (x – 2) leave the same remainder, Find the value of a
Sol :
Here , the polynomials are
f(x) = ax3+3x2–13
p(x) = 2x3–5x+a
equate , x – 2 = 0
x = 2
substitute the value of x in f(x) and p(x)
f(2) = (2)3+3(2)2–13
= 8a + 12 – 13
= 8a – 1 ———- 1
p(2) = 2(2)3–5(2)+a
= 16 – 10 + a
= 6 + a ———– 2
f(2) = p(2)
⇒ 8a – 1 = 6 + a
⇒ 8a – a = 6 + 1
⇒ 7a = 7
⇒ a = 1
The value of a = 1
Q12. Find the remainder when x3+3x3+3x+1 is divided by,
1. x + 1
2. 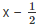
3. x
4. x + π
5. 5 + 2x
Sol :
Here, f(x) = x3+3x2+3x+1
by remainder theorem
1. ⇒ x + 1 = 0
⇒ x = -1
substitute the value of x in f(x)
f(-1) = (−1)3+3(−1)2+3(−1)+1
= -1 + 3 – 3 + 1
= 0
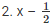
Here, f(x) = x3+3x2+3x+1
By remainder theorem
⇒ 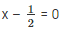
⇒ 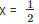
substitute the value of x in f(x)

= 27/8
3. x
Sol :
Here, f(x) = x3+3x2+3x+1
by remainder theorem
⇒ x = 0
substitute the value of x in f(x)
f(0) = 03+3(0)2+3(0)+1
= 0 + 0 + 0 + 1
= 1
4. x + π
Sol :
Here, f(x) = x3+3x2+3x+1
by remainder theorem
⇒ x + π = 0
⇒ x = -π
Substitute the value of x in f(x)
f(-π) = (−π)3+3(−π)2+3(−π)+1
= –(π)3+3(π)2–3(π)+1
5. 5 + 2x
Sol :
Here, f(x) = x3+3x2+3x+1
by remainder theorem
5 + 2x = 0
2x = -5
x = -5/2
substitute the value of x in f(x)
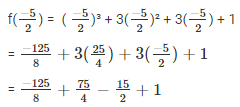
Taking L.C.M
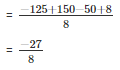
FAQs on RD Sharma Solutions Ex-6.3, Factorization Of Polynomials, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of factorization of polynomials in mathematics? |  |
| 2. How can factorization of polynomials be used to solve real-world problems? |  |
| 3. What are the methods used for factorization of polynomials? |  |
| 4. Can all polynomials be factored completely? |  |
| 5. How does factorization of polynomials relate to finding the roots of a polynomial equation? |  |
















