RD Sharma Solutions Ex-6.4, (Part -1), Factorization Of Polynomials, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
In each of the following, use factor theorem to find whether polynomial g(x) is a factor of polynomial f(x) , or not : (1 – 7)
Q1. f(x) = x3–6x2+11x–6,g(x) = x–3
Sol :
Here , f(x) = x3–6x2+11x–6
g(x) = x – 3
To prove that g(x) is the factor of f(x) ,
we should show ⇒ f(3) = 0
here , x – 3 = 0
⇒ x = 3
Substitute the value of x in f(x)
f(3) = 33–6∗(3)2+11(3)–6
= 27 – (6*9) + 33 – 6
= 27 – 54 + 33 – 6
= 60 – 60
= 0
Since, the result is 0 g(x) is the factor of f(x)
Q2. f(x) = 3x4+17x3+9x2–7x–10,g(x) = x+5
Sol :
Here , f(x) = 3x4+17x3+9x2–7x–10
g(x) = x + 5
To prove that g(x) is the factor of f(x) ,
we should show ⇒ f(-5) = 0
here , x + 5 = 0
⇒ x = -5
Substitute the value of x in f(x)
f(−5)=3(−5)4+17(−5)3+9(−5)2–7(−5)–10
= (3 * 625) + (12 * (-125)) +(9*25) + 35 – 10
= 1875 – 2125 + 225 + 35 – 10
= 2135 – 2135
= 0
Since, the result is 0 g(x) is the factor of f(x)
Q3. f(x) = x5+3x4–x3–3x2+5x+15,g(x) = x+3
Sol :
Here , f(x) = x5+3x4–x3–3x2+5x+15
g(x) = x + 3
To prove that g(x) is the factor of f(x) ,
we should show ⇒ f(-3) = 0
here , x + 3 = 0
⇒ x = -3
Substitute the value of x in f(x)
f(−3)=(−3)5+3(−3)4–(−3)3–3(−3)2+5(−3)+15
= -243 + 243 + 27 – 27 – 15 + 15
= 0
Since, the result is 0 g(x) is the factor of f(x)
Q4. f(x) = x3–6x2–19x+84,g(x)=x–7
Sol :
Here , f(x) = x3–6x2–19x+84
g(x) = x – 7
To prove that g(x) is the factor of f(x) ,
we should show ⇒ f(7) = 0
here , x – 7 = 0
⇒ x = 7
Substitute the value of x in f(x)
f(7) = 73–6(7)2–19(7)+84
= 343 – (6*49) – (19*7) + 84
= 342 – 294 – 133 + 84
= 427 – 427
= 0
Since, the result is 0 g(x) is the factor of f(x)
Q5. f(x) = 3x3+x2–20x+12,g(x) = 3x–2
Sol :
Here , f(x)=3x3+x2–20x+12
g(x) = 3x – 2
To prove that g(x) is the factor of f(x) ,
we should show ⇒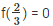 
here , 3x – 2 = 0
⇒ 3x = 2
⇒ x = 2/3
Substitute the value of x in f(x)
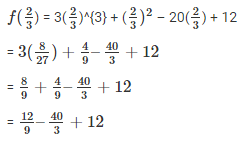
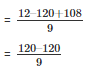
= 0
Since, the result is 0 g(x) is the factor of f(x)
Q6. f(x) = 2x3–9x2+x+13,g(x) = 3–2x
Sol :
Here , f(x) = 2x3–9x2+x+13
g(x) = 3 – 2x
To prove that g(x) is the factor of f(x) ,
To prove that g(x) is the factor of f(x) ,
we should show ⇒ f(3/2) = 0
here , 3 – 2x = 0
⇒ -2x = -3
⇒ 2x = 3
⇒ x = 3/2
Substitute the value of x in f(x)
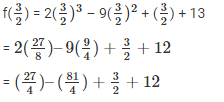
Taking L.C.M
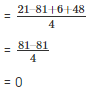
Since, the result is 0 g(x) is the factor of f(x)
Q7. f(x) = x3–6x2+11x–6,g(x) = x2–3x+2
Sol :
Here , f(x) = x3–6x2+11x–6
g(x) = x2–3x+2
First we need to find the factors of x2–3x+2
⇒ x2–2x–x+2
⇒ x(x – 2) -1(x – 2)
⇒ (x – 1) and (x – 2) are the factors
To prove that g(x) is the factor of f(x) ,
The results of f(1) and f(2) should be zero
Let , x – 1 = 0
x = 1
substitute the value of x in f(x)
f(1) = 13–6(1)2+11(1)–6
= 1 – 6 + 11 – 6
= 12 – 12
= 0
Let , x – 2 = 0
x = 2
substitute the value of x in f(x)
f(2) = 23–6(2)2+11(2)–6
= 8 – (6 * 4) + 22 – 6
= 8 – 24 + 22 – 6
= 30 – 30
= 0
Since, the results are 0 g(x) is the factor of f(x)
Q8. Show that (x – 2) , (x + 3) and (x – 4) are the factors of x3–3x2–10x+24
Sol :
Here , f(x) = x3–3x2–10x+24
The factors given are (x – 2) , (x + 3) and (x – 4)
To prove that g(x) is the factor of f(x) ,
The results of f(2) , f(-3) and f(4) should be zero
Let , x – 2 = 0
⇒ x = 2
Substitute the value of x in f(x)
f(2) = 23–3(2)2–10(2)+24
= 8 – (3 * 4) – 20 + 24
= 8 – 12 – 20 + 24
= 32 – 32
= 0
Let , x + 3 = 0
⇒ x = -3
Substitute the value of x in f(x)
f(-3) = (−3)3–3(−3)2–10(−3)+24
= -27 – 3(9) + 30 + 24
= -27 – 27 + 30 + 24
= 54 – 54
= 0
Let , x – 4 = 0
⇒ x = 4
Substitute the value of x in f(x)
f(4) = (4)3–3(4)2–10(4)+24
= 64 – (3*16) – 40 + 24
= 64 – 48 – 40 + 24
= 84 – 84
= 0
Since, the results are 0 g(x) is the factor of f(x)
Q9. Show that (x + 4) , (x – 3) and (x – 7) are the factors of x3–6x2–19x+84
Sol :
Here , f(x) = x3–6x2–19x+84
The factors given are (x + 4) , (x – 3) and (x – 7)
To prove that g(x) is the factor of f(x) ,
The results of f(-4) , f(3) and f(7) should be zero
Let, x + 4 = 0
⇒ x = -4
Substitute the value of x in f(x)
f(-4) = (−4)3–6(−4)2–19(−4)+84
= -64 – (6 * 16) – ( 19 * (-4)) + 84
= -64 – 96 + 76 + 84
= 160 – 160
= 0
Let, x – 3 = 0
⇒ x = 3
Substitute the value of x in f(x)
f(3) = (3)3–6(3)2–19(3)+84
= 27 – (6 * 9) – ( 19 * 3) + 84
= 27 – 54 – 57 + 84
= 111 – 111
= 0
Let, x – 7 = 0
⇒ x = 7
Substitute the value of x in f(x)
f(7) = (7)3–6(7)2–19(7)+84
= 343 – (6 * 49) – ( 19 * 7) + 84
= 343 – 294 – 133 + 84
= 427 – 427
= 0
Since, the results are 0 g(x) is the factor of f(x)
Q10. For what value of a is (x – 5) a factor of x3–3x2+ax–10
Sol :
Here, f(x) = x3–3x2+ax–10
By factor theorem
If (x – 5) is the factor of f(x) then , f(5) = 0
⇒ x – 5 = 0
⇒ x = 5
Substitute the value of x in f(x)
f(5) = 53–3(5)2+a(5)–10
= 125 – (3 * 25) + 5a – 10
= 125 – 75 + 5a – 10
= 5a + 40
Equate f(5) to zero
f(5) = 0
⇒ 5a + 40 = 0
⇒ 5a = -40
⇒ 
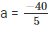
= -8
When a= -8 , (x – 5) will be factor of f(x)
Q11. Find the value of a such that (x – 4) is a factor of 5x3–7x2–ax–28
Sol :
Here, f(x) = 5x3–7x2–ax–28
By factor theorem
If (x – 4) is the factor of f(x) then , f(4) = 0
⇒ x – 4 = 0
⇒ x = 4
Substitute the value of x in f(x)
f(4) = 5(4)3–7(4)2–a(4)–28
= 5(64) – 7(16) – 4a – 28
= 320 – 112 – 4a – 28
= 180 – 4
Equate f(4) to zero, to find a
f(4) = 0
⇒ 180 – 4a = 0
⇒ -4a = -180
⇒ 4a = 180
⇒ a = 180/4
⇒ a = 45
When a = 45 , (x – 4) will be factor of f(x)
Q12. Find the value of a, if (x + 2) is a factor of 4x4+2x3–3x2+8x+5a
Sol :
Here, f(x) = 4x4+2x3–3x2+8x+5a
By factor theorem
If (x + 2) is the factor of f(x) then , f(-2) = 0
⇒ x + 2 = 0
⇒ x = -2
Substitute the value of x in f(x)
f(-2) = 4(−2)4+2(−2)3–3(−2)2+8(−2)+5a
= 4(16) + 2(-8) – 3( 4) – 16 + 5a
= 64 – 16 – 12 – 16 + 5a
= 5a + 20
equate f(-2) to zero
f(-2) = 0
⇒ 5a + 20 = 0
⇒ 5a = -20
⇒ 
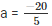
⇒ a = -4
When a = -4 , (x + 2) will be factor of f(x)
Q13. Find the value of k if x – 3 is a factor of k2x3–kx2+3kx–k
Sol :
Let f(x) = k2x3–kx2+3kx–k
From factor theorem if x – 3 is the factor of f(x) then f(3) = 0
⇒ x – 3 = 0
⇒ x = 3
Substitute the value of x in f(x)
f(3) = k2(3)3–k(3)2+3k(3)–k
= 27k2–9k+9k – k
= 27k2–k
= k(27k – 1)
Equate f(3) to zero, to find k
⇒ f(3) = 0
⇒ k(27k – 1) = 0
⇒ k = 0 and 27k – 1 = 0
⇒ k = 0 and 27k = 1
⇒ k = 0 and k = 12/7
When k = 0 and 12/7 , (x – 3) will be the factor of f(x)
FAQs on RD Sharma Solutions Ex-6.4, (Part -1), Factorization Of Polynomials, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of factorization of polynomials in mathematics? |  |
| 2. How can I factorize a polynomial using the common factor method? | |
| 3. What are the different methods of factorizing polynomials? | |
| 4. Can all polynomials be factorized? | |
| 5. How can factorization of polynomials be applied in real-life situations? | |
|
4.61/5 Rating |
|
Nov 24, 2024 Last updated |
|
Explore Courses for Class 9 exam
|
|
Class 9
,(Part -1)
,Exam
,Class 9
,Maths | RD Sharma Solutions for Class 9 Mathematics
,Viva Questions
,past year papers
,(Part -1)
,ppt
,RD Sharma Solutions Ex-6.4
,RD Sharma Solutions Ex-6.4
,MCQs
,Factorization Of Polynomials
,Previous Year Questions with Solutions
,shortcuts and tricks
,Free
,Important questions
,Objective type Questions
,study material
,Sample Paper
,mock tests for examination
,Factorization Of Polynomials
,practice quizzes
,RD Sharma Solutions Ex-6.4
,Maths | RD Sharma Solutions for Class 9 Mathematics
,Summary
,Semester Notes
,video lectures
,Maths | RD Sharma Solutions for Class 9 Mathematics
,(Part -1)
,Class 9
,Extra Questions
,Factorization Of Polynomials
;
RD Sharma Solutions Ex-6.4, (Part -1), Factorization Of Polynomials, Class 9, Maths Free PDF Download
Importance of RD Sharma Solutions Ex-6.4, (Part -1), Factorization Of Polynomials, Class 9, Maths
RD Sharma Solutions Ex-6.4, (Part -1), Factorization Of Polynomials, Class 9, Maths Notes
RD Sharma Solutions Ex-6.4, (Part -1), Factorization Of Polynomials, Class 9, Maths Class 9 Questions
Study RD Sharma Solutions Ex-6.4, (Part -1), Factorization Of Polynomials, Class 9, Maths on the App
|
© EduRev
|
Education Revolution
|
Follow Us
|
within 7 days!