RD Sharma Solutions Ex-7.1, Introduction To Euclid's Geometry, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q. 1. Define the following terms.
(i) Line segment
(ii) Collinear points
(iii) Parallel lines
(iv) Intersecting lines
(v) Concurrent lines
(vi) Ray
(vii) Half-line
Solution
(i) Line-segment:
Give two points A and B on a line I. the connected part (segment) of the line with end points at A and B is called the line segment AB.

(ii) Collinear points:
Three or more points are said to be collinear if there is a line which contains all of them.

(iii) Parallel lines:
Two lines l and m in a plane are said to be parallel lines if they do not intersect each other.

(iv) Intersecting lines:
Two lines are intersecting if they have a common point. The common point is called point of intersection.
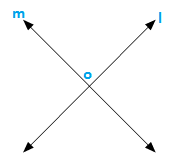
(v) Concurrent lines:
Three or more lines are said to be concurrent if there is a point which lies on all of them.
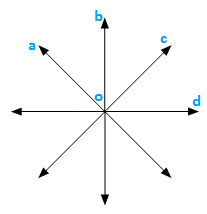
(vi) Ray:
A line in which one end point is fixed and the other part can be extended endlessly.

(vii) Half-line:
If A, B. C be the points on a line l, such that A lies between B and C, and we delete the point A from line l, the two parts of l that remain are each called half-line.

Q. 2. (i) How many lines can pan through a given point?
(ii) In how many points can two distinct lines at the most intersect?
Solution
(i) Infinitely many
(ii) One
Q. 3. (i) Given two points P and Q. Find how many line segments do they determine.
(ii) Name the line segments determined by the three collinear points P. Q and R.
Solution
(i) One
(ii) PQ, QR, PR
Q. 4. Write the truth value (T/F) of each of the following statements:
(i) Two lines intersect in a point.
(ii) Two lines may intersect in two points
(iii) A segment has no length.
(iv) Two distinct points always determine a line.
(v) Every ray has a finite length.
(vi) A ray has one end-point only.
(vii) A segment has one end-point only.
(viii) The ray AB is same as ray BA.
(ix) Only a single line may pass through a given point.
(x) Two lines are coincident if they have only one point in common
Solution
(i) False
(ii) False
(iii) False
(iv) True
(v) False
(vi) True
(vii) False
(viii) False
(ix) False
(x) False
Q. 5. In the below figure. Name the following:
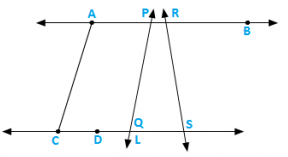
Solution:
(i) Five line segments AB, CD, AC, PQ. DS
(ii) Five rays →PA,→RB,→DC,→QS,→DS
(iii) Four collinear points. C, D, Q, S
(iv) Two pairs of non–intersecting line segments AB and CD, AB and LS.
Q. 6. Fill in the blanks so as to make the following statements true:
(i) Two distinct points in a plane determine a _____________ line.
(ii) Two distinct ___________ in a plane cannot have more than one point in common.
(iii) Given a line and a point, not on the line, there is one and only _____________ line which passes through the given point and is _______________ to the given line.
(iv) A line separates a plane into _________ parts namely the __________ and the _____ itself.
Solution
(i) Unique
(ii) Lines
(iii) Perpendicular, perpendicular
(iv) Three, two half planes, line.
FAQs on RD Sharma Solutions Ex-7.1, Introduction To Euclid's Geometry, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is Euclid's Geometry? |  |
| 2. Who was Euclid and why is he important in the field of geometry? |  |
| 3. What are the key elements of Euclid's Geometry? |  |
| 4. How did Euclid's Geometry contribute to the development of mathematics? |  |
| 5. Can Euclid's Geometry be applied in real-life situations? |  |
















