RD Sharma Solutions Ex-8.1, Lines And Angles, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 1 : Write the complement of each of the following angles:
(i)20∘
(ii)35∘
(iii)90∘
(iv)77∘
(v)30∘
Ans : (i) given angle is 20
Since, the sum of an angle and its compliment is 90
Hence, its compliment will be (90 – 20 = 70)
(ii) Given angle is 35
Since, the sum of an angle and its compliment is 90
Hence, its compliment will be (90 – 35 = 55)
(iii) Given angle is 90
Since, the sum of an angle and its compliment is 90
Hence, its compliment will be (90 – 90 = 0)
(iv) Given angle is 77
Since, the sum of an angle and its compliment is 90
Hence, its compliment will be (90 – 77 = 13)
(v) Given angle is 30
Since, the sum of an angle and its compliment is 90
Hence, its compliment will be (90 – 30 = 60)
Q 2 : Write the supplement of each of the following angles:
(i) 54∘
(ii) 132∘
(iii) 138∘
Ans : (i) The given angle is 54,
Since the sum of an angle and its supplement is 180,
Hence, Its supplement will be (180 – 54 = 126)
(ii) The given angle is 132,
Since the sum of an angle and its supplement is 180,
Hence, its supplement will be 180 – 132 = 48
(iii) The given angle is 138,
Since the sum of an angle and its supplement is 180,
Hence, Its supplement will be 180 – 138 = 42
Q 3 : If an angle is 28∘ less than its complement, find its measure?
Ans: Let the angle measured be ‘ x ‘ in degrees
Hence, Its complement will be 90−x∘
- Angle = Complement – 28
- x = (90 – x) – 28
- 2x = 62
- x = 31
Therefore, angle measured is 31∘
Q 4 : If an angle is 30∘ more than half of its complement, find the measure of the angle?
Ans : Let the measured angle be ‘x‘
Hence its complement will be (90-x)
It is given that,
Angle =30 + complement/2
- x = 30 + (90 – x) / 2
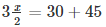
- 3x = 150
- x = 50
Therefore the angle is 50∘
Q 5 : Two supplementary angles are in the ratio 4:5.Find the angles?
Ans : Supplementary angles are in the ratio 4:5
Let the angles be 4x and 5x
It is given that they are supplementary angles
Hence 4x + 5x = 180
- 9x = 180
- x = 20
Hence, 4x = 4 (20) = 80
5(x) = 5 (20) = 100
Hence, angles are 80 and 100
Q 6 : Two supplementary angles differ by 48∘.Find the angles ?
Ans : Given that two supplementary angles differ by 48∘
Let the angle measured be x∘
Therefore, Its supplementary angle will be (180−x)∘
It is given that :
- (180 – x) – x = 48
- (180 – 48) = 2x
- 2 x = 132
- x = 132/2
- x = 66
Hence, 180 – x = 114∘
Therefore, the angles are 66 and 114.
Q 7 : An angle is equal to 8 times its complement. Determine its measure?
Ans : It is given that required angle = 8 times its complement
Let ‘ x ‘ be the measured angle
- angle = 8 times complement
- angle = 8 (90 – x)
- x = 8 (90 – x )
- x = 720 – 8x
- x + 8x = 720
- 9x = 720
- x = 80
Therefore measured angle is 80.
Q 8 : If the angles (2x−10)∘ and (x−5)∘ are complementary, find x ?
Ans : Given that (2x−10)∘ and (x−5)∘ are complementary
Since angles are complementary, their sum will be 90
- (2x – 10) + (x – 5) = 90
- 3x -15 = 90
- 3x = 90 + 15
- 3x = 105
- x = 105/3
- x = 35
Hence, the value of x = (35)∘
Q 9 : If the compliment of an angle is equal to the supplement of Thrice of itself, find the measure of the angle ?
Ans : Let the angle measured be ‘ x ‘ say.
Its complementary angle is (90 – x) and
Its supplementary angle is (180 – 3x)
Given that, Supplementary of 4 times the angle = (180 – 3x)
According to the given information;
- (90 – x) = (180 – 3x)
- 3x – x = 180 – 90
- 2x = 90
- x = 90/2
- x = 45
Therefore, the measured angle x = (45)∘
Q 10 : If an angle differs from its complement by (10)∘, find the angle ?
Ans : Let the measured angle be ‘ x ‘ say
Given that,
The angles measured will differ by (20)∘
x – (90 – x) = 10
- x – 90 + x = 10
- 2x = 90 + 10
- 2x = 100
- x = 100/2
- x = 50
Therefore the measure of the angle is (50)∘
Q 11 : If the supplement of an angle is 3 times its complement, find its angle ?
Ans : Let the angle in case be ‘ x ‘
Given that,
Supplement of an angle = 3 times its complementary angle
Supplementary angle = 180 – x
Complementary angle = 90 – x
Applying given data,
- 180 – x = 3 (90 –x)
- 3x – x = 270 – 180
- 2x = 90
- x = 90/2
- x = 45
Therefore, the angle in case is 45∘
Q 12 : If the supplement of an angle is two third of itself. Determine the angle and its supplement?
Ans: Supplementary of an angle = 2/3 angle
Let the angle in case be ‘ x ’,
Supplementary of angle x will be ( 180 – x)
It is given that
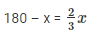
- (180 – x) 3 = 2x
- 540 -3x = 2x
- 5x = 540
- x = 540/5
- x = 108
Hence, supplementary angle = 180 – 108 = 72
Therefore, angles in case are 108∘ and supplementary angleis 72∘
Q 13 : An angle is 14∘ more than its complementary angle. What is its measure?
Ans: Let the angle in case be ‘ x ’,
Complementary angle of ‘ x ’ is ( 90 – x)
From given data,
x – (90 – x) = 14
- x – 90 +x = 14
- 2x = 90 + 14
- 2x = 104
- x =104/2
- x = 52
Hence the angle in case is found to be 52∘
Q 14 : The measure of an angle is twice the measure of its supplementary angle. Find the measure of the angles?
Ans : Let the angle in case be ‘ x ’
The supplementary of a angle x is (180 – x)
Applying given data:
x = 2 (180 –x)
- x = 360 -2x
- 3x = 360
- x = 360/3
- x = 120
Therefore the value of the angle in case is 120∘
FAQs on RD Sharma Solutions Ex-8.1, Lines And Angles, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are the types of angles? |  |
| 2. How do you identify complementary angles? |  |
| 3. What is the difference between adjacent angles and linear pair angles? |  |
| 4. How do you find the measure of an angle using a protractor? |  |
| 5. Can two obtuse angles be adjacent angles? |  |
















