Exercise 2.3 - Powers RD Sharma Solutions | Mathematics (Maths) Class 8 PDF Download
Q.1. Express the following numbers in standard form:
(i) 6020000000000000
(ii) 0.00000000000943
(iii) 0.00000000085
(iv) 846 × 107
(v) 3759 × 10−4
(vi) 0.00072984
(vii) 0.000437 × 104
(viii) 4 ÷ 100000
Ans: To express a number in the standard form, move the decimal point such that there is only one digit to the left of the decimal point.
(i) 6020000000000000 = 6.02 x 1015(The decimal point is moved 15 places to the left.)
(ii) 0.0000000000943 = 9.43 x 10−12(The decimal point is moved 12 places to the right.)
(iii) 0.00000000085 = 8.5 x 10−10(The decimal point is moved 10 places to the right.)
(iv) 846 x 107 = 8.46 x 102 x 107 = 8.46 x 109 (The decimal point is moved two places to the left.)
(v) 3759 x 10−4 = 3.759 x 103 x 10−4 = 3.759 x 10−1(The decimal point is moved three places to the left.)
(vi) 0.00072984 = 7.984 x 10−4(The decimal point is moved four places to the right.)
(vii) 0.000437 x 104 = 4.37 x 10−4 x 104 = 4.37 x 100 = 4.37(The decimal point is moved four places to the right.)
(viii) 4/100000 = 4 x 100000−1 = 4 x 10−5(Just count the number of zeros in 1,00,000 to determine the exponent of 10.)
Q.2. Write the following numbers in the usual form:
(i) 4.83 × 107
(ii) 3.02 × 10−6
(iii) 4.5 × 104
(iv) 3 × 10−8
(v) 1.0001 × 109
(vi) 5.8 × 102
(vii) 3.61492 × 106
(viii) 3.25 × 10−7
Ans:
(i) 4.83 x 107 = 4.83 x 1,00,00,000 = 4,83,00,000
(ii) 3.02 x 10−6 = 3.02/106 = 3.02/10,00,000 = 0.00000302
(iii) 4.5 x 104 = 4.5 x 10,000 = 45,000
(iv) 3 x 10−8 = 3/108 = 3/10,00,00,000 = 0.00000003
(v) 1.0001 x 109 = 1.0001 x 1,00,00,00,000 = 1,00,01,00,000
(vi) 5.8 x 102 = 5.8 x 100 = 580
(vii) 3.61492 x 106 = 3.61492 x 10,00,000 = 3614920
(viii) 3.25 x 10−7 = 3.25/107 = 3.25/1,00,00,000 = 0.000000325
Exercise (MCQs)
Q.1. Square of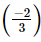 is
is
(a) −2/3
(b) 2/3
(c) −4/9
(d) 4/9
Ans: (d) 4/9
To square a number is to raise it to the power of 2. Hence, the square of (−2/3) is
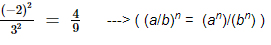
Q.2. Cube of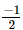 is
is
(a) 1/8
(b) 1/16
(c) −1/8
(d) −1/16
Ans: (c) -1/8
The cube of a number is the number raised to the power of 3. Hence the cube of −1/2 is
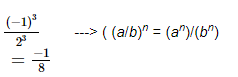
Q.3. Which of the following is not equal to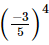 ?
?
(a)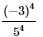
(b)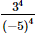
(c)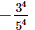
(d)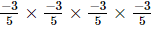
Ans:
(c) −(34/54)
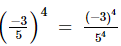 =
= 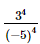 =
= 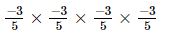
It is not equal to −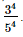
Q.4. Which of the following is not reciprocal of (2/3)4?
(a)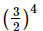
(b)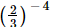
(c)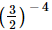
(d)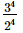
Ans:
(c) (3/2)−4
The reciprocal of 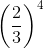 is
is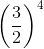
Therefore, option (a) is the correct answer.
Option (b) is just re-expressing the number with a negative exponent.
Option (d) is obtained by working out the exponent.
Hence,option (c) is not the reciprocal of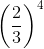
Q.5. Which of the following numbers is not equal to −8/27?
(a)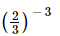
(b)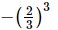
(c)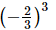
(d)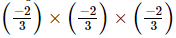
Ans:
(a) (2/3)-3
We can write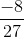 as
as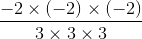 . It can be written in the forms given below.
. It can be written in the forms given below.
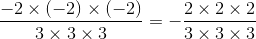 ---> work out the minuses
---> work out the minuses

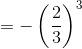
Hence, option (b) is equal to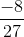
We can also write:
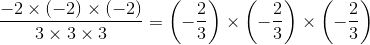
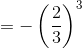
Hence, option (c) is also equal to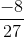
We can also write:
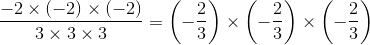
Hence, option (d) is also equal to −8/27.
This leaves out option (a) as the one not equal to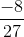 .
.
Q.6. 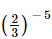 is equal to
is equal to
(a)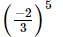
(b)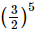
(c)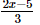
(d)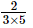
Ans:
(b)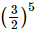
Rearrange (2/3)−5 to get a positive exponent.
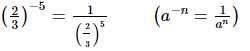
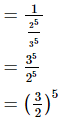
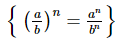
Q.7. 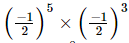 is equal to
is equal to
(a)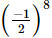
(b)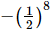
(c)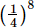
(d)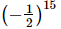
Ans:
(a) (−1/2)8
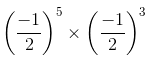 =
= 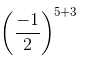
= 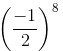
Q.8. 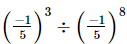 is equal to
is equal to
(a)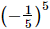
(b)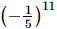
(c)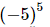
(d)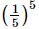
Ans:
(c) (−5)5
We have:
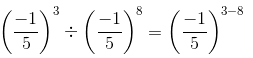
=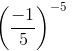
=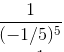
= 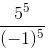
= 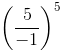
=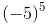
Q.9. 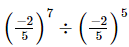 is equal to
is equal to
(a) 4/25
(b) −4/25
(c) (−2/5)12
(d) 25/4
Ans:
(a) 4/25
We have:
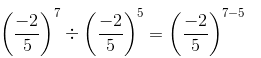
=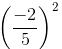
=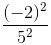
=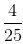
Q.10. 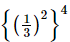 is equal to
is equal to
a) (1/3)6
(b) (1/3)8
(c) (1/3)24
(d) (1/3)16
Ans:
(b) (1/3)8
We have:
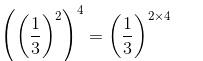
=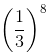
Q.11. 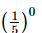 is equal to
is equal to
(a) 0
(b) 1/5
(c) 1
(d) 5
Ans:
(c) 1
We have:
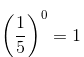 --> (a0 = 1, for every non-zero rational number a.)
--> (a0 = 1, for every non-zero rational number a.)
Q.12. 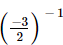 is equal to
is equal to
(a) 2/3
(b) −2/3
(c) 3/2
(d) none of these
Ans:
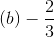
We have:
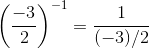
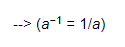
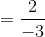
Q.13.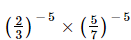 is equal to
is equal to
(a)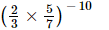
(b)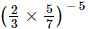
(c)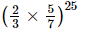
(d)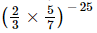
Ans:
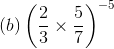
We have:
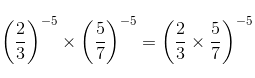
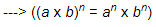
Q.14. 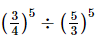 is equal to
is equal to
Ans:
(a) 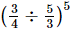
We have;
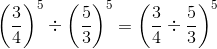
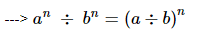
Q.15. For any two non-zero rational numbers a and b, a4 ÷ b4 is equal to
(a) (a ÷ b)1
(b) (a ÷ b)0
(c) (a ÷ b)4
(d) (a ÷ b)8
Ans:
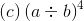
This is one of the basic exponential formulae, i.e.
Q.16. For any two rational numbers a and b, a5 × b5 is equal to
(a) (a × b)0
(b) (a × b)10
(c) (a × b)5
(d) (a × b)25
Ans:
(c) (a x b)5
an x bn = (a x b)n
Hence,
a5 x b5 = (a x b)5
Q.17. For a non-zero rational number a, a7 ÷ a12 is equal to
(a) a5
(b) a−19
(c) a−5
(d) a19
Ans:
(c) a−5
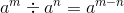
Hence,
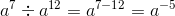
Q.18. For a non zero rational number a, (a3)−2 is equal to
(a) a9
(b) a−6
(c) a−9
(d) a1
Ans:
(b) a−6
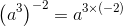
= a-6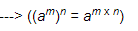
|
79 videos|408 docs|31 tests
|
FAQs on Exercise 2.3 - Powers RD Sharma Solutions - Mathematics (Maths) Class 8
| 1. What is the importance of powers in mathematics? |  |
| 2. How do you calculate the power of a number? |  |
| 3. What is the significance of the exponent in a power? |  |
| 4. How do you simplify expressions involving powers? |  |
| 5. How are powers used in real-life situations? |  |

|
Explore Courses for Class 8 exam
|

|

















