Exponents of Real Numbers- 2 RD Sharma Solutions | Mathematics (Maths) Class 9 PDF Download
RD Sharma Solutions Exercise 2.2 Exponents Of Real Numbers
Q.1. Assuming that x, y, z are positive real numbers, simplify each of the following:
(i) (√x−3)5
(ii) √x3 y−2
(iii) (x−2/3y−1/2)2
(iv) (√x)−2/3√y4 ÷ √xy−1/2
(v) 5√243 x10y5z10
(vi) 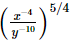
(vii) 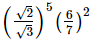
Proof: We have to simplify the following, assuming that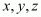 are positive real numbers
are positive real numbers
(i) Given
As x is positive real number then we have
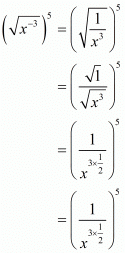
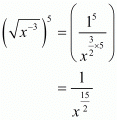
Hence the simplified value of is
is
(ii) Given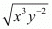
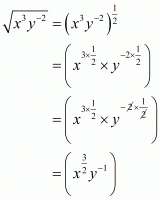
By using law of rational exponents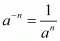 we have
we have
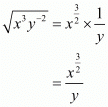
Hence the simplified value of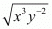 is
is
(iii) Given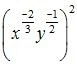
As x and y are positive real numbers then we have

By using law of rational exponents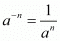 we have
we have
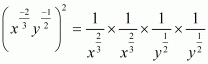
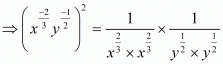
By using law of rational exponents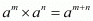 we have
we have
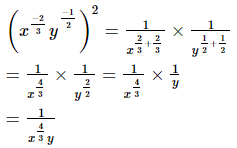
Hence the simplified value of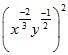 is
is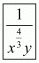
(iv)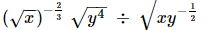
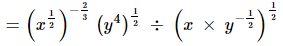
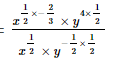
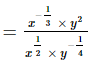
by using the law of rational exponents, am ÷ an = am−n, we have
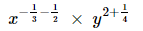
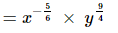
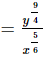
(v)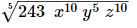
=(243 × x10 × y5 × z10)1/5
=(243)1/5 × (x10)1/5 × (y5)1/5 × (z10)1/5
=(35)1/5 × x10×1/5 × y5×1/5 × z10×1/5
=3 × x2 × y × z2
=3x2yz2
(vi)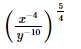
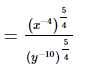
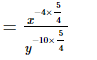
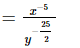
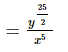
(vii)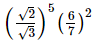

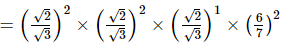
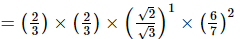

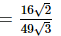
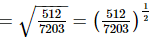
Q.2. Simplify:
(i)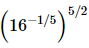
(ii)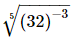
(iii)
(v)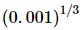
(v)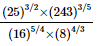
(vi)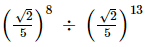
(vii)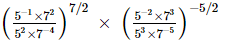
Proof: (1) Given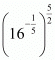
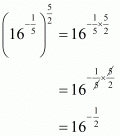
By using law of rational exponents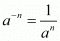 we have
we have
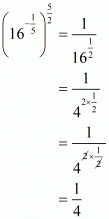
Hence the value of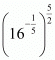 is
is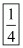
(ii)
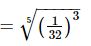

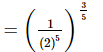
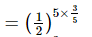
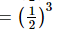
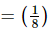
(iii) Given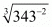
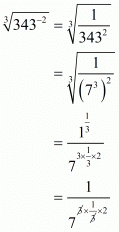
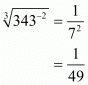
Hence the value of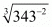 is
is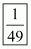
(iv) Given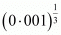
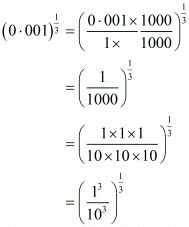

The value of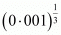 is
is 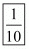
(v) Given
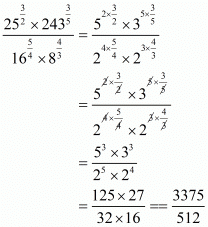
(vi) Given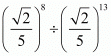 So,
So,
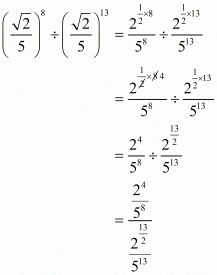
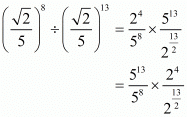
By using the law of rational exponents
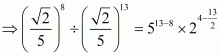
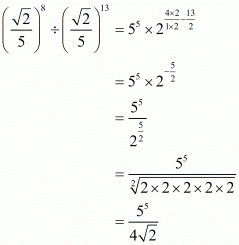
Hence the value of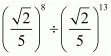 is
is
(vii) Given So,
So,
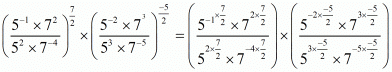
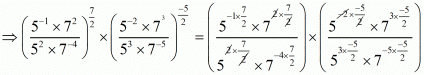
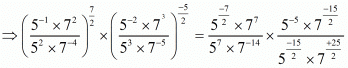
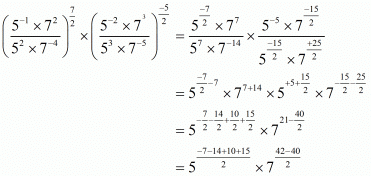
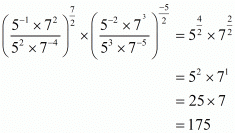
Hence the value of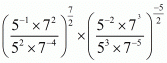 is
is
Q.3. Prove that:
(i)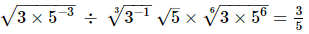
(ii)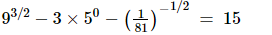
(iii)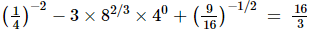
(iv)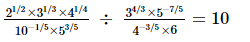
(v)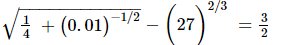
(vi)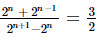
(vii)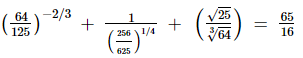
(viii)
(ix)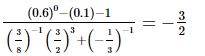
Proof: (i) We have to prove that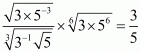
By using rational exponent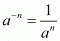 we get,
we get,
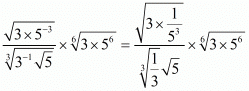
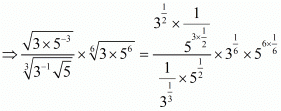
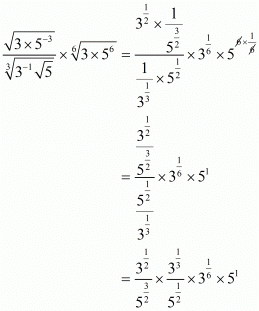
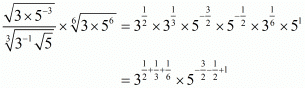
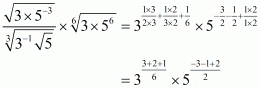
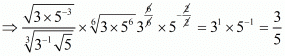
Hence,
(ii) We have to prove that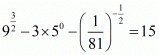
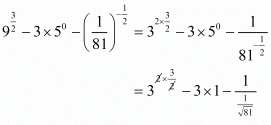
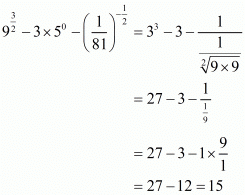
Hence,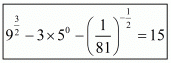
iii) We have to prove that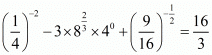
Now,
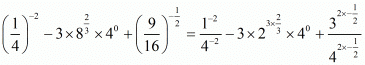
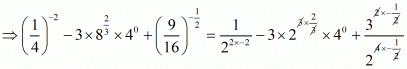
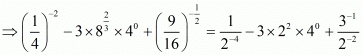
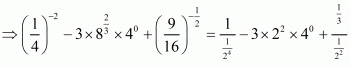
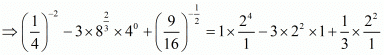
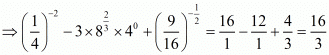
Hence,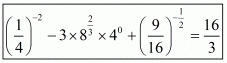
(iv) We have to prove that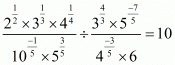
Let 
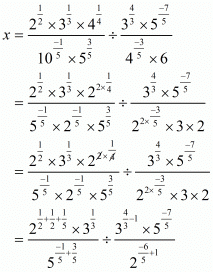
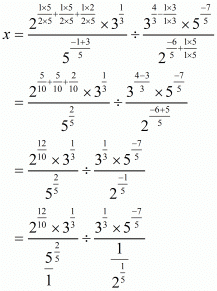
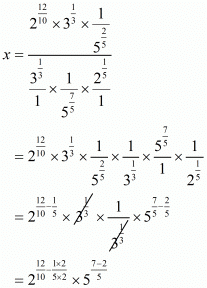
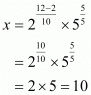
Hence,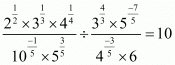
(v) We have to prove that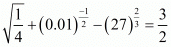
Let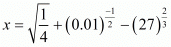
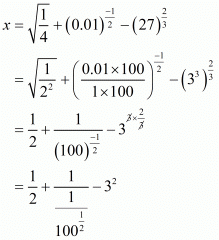


Hence,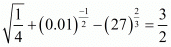
(vi) We have to prove that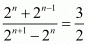 So,
So,
Let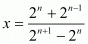
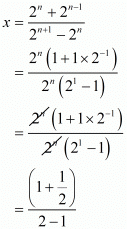
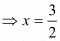
Hence,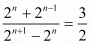
(vii) We have to prove that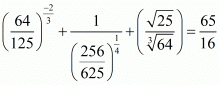 So let
So let
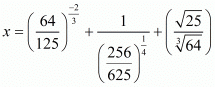
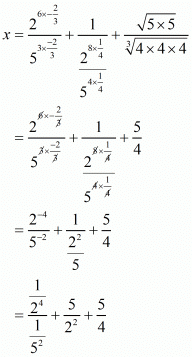
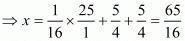
Hence, 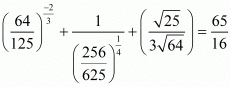
(viii) We have to prove that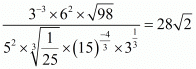 So,
So,
Let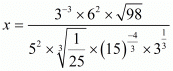
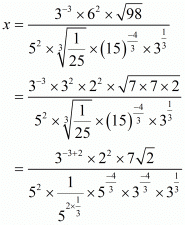
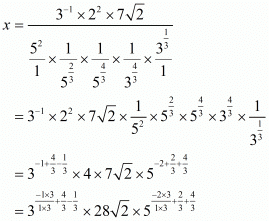
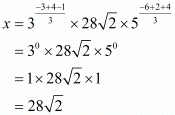
Hence,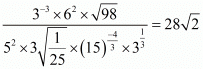
(ix) We have to prove that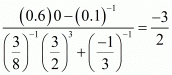
Let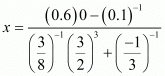
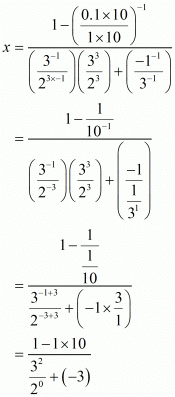
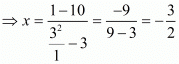
Hence,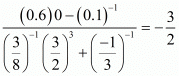
Q.4. Show that:
(i)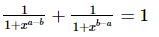
(ii)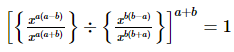
(iii)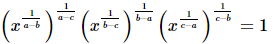
(iv)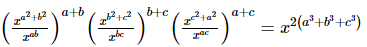
(v)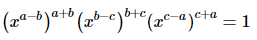
(vi)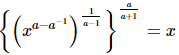
(vii)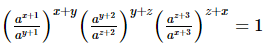
(viii)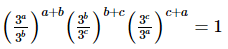
Proof: (i)
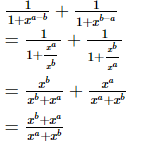
= 1
(ii)
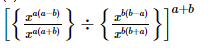
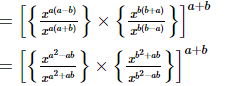
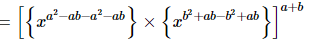
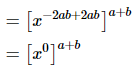
= 1
(iii)
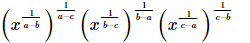
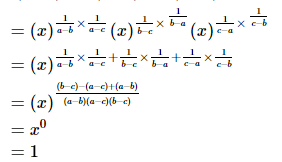
(iv)
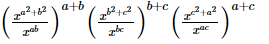
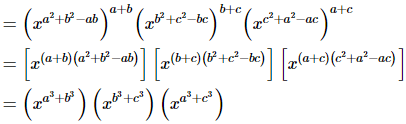
=x2(a3+b3+c3)
(v)
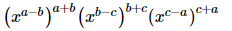
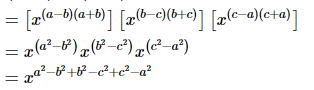
= x0
= 1
(vi)

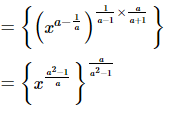
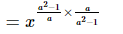
= x1
= x
(vii)
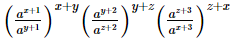
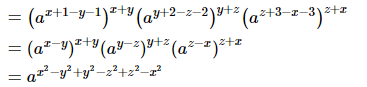
=a0
=1
(viii)
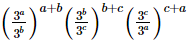
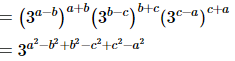
=30
=1
Q.5. If 27x =9/3x, find x
Proof: We are given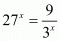 We have to find the value of x
We have to find the value of x
Since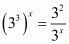
y using the law of exponents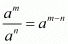 we get,
we get,

On equating the exponents we get,
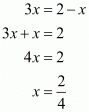
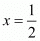
Hence,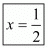
Q.6. Find the values of x in each of the following:
(i)
(ii)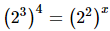
(iii)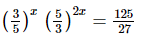
(iv)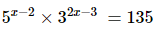
(v)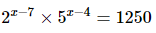
(vi)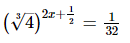
(vii) 52x+3=1
(viii)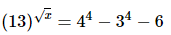
(ix)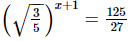
Proof: From the following we have to find the value of x
(i) Given
By using rational exponents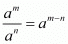
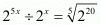
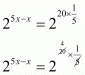
On equating the exponents we get,
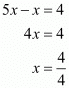
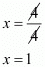
The value of x is
(ii) Given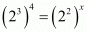
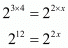
On equating the exponents
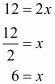
Hence the value of x is
(iii) Given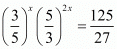
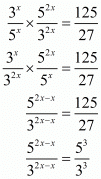
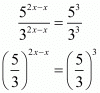
Comparing exponents we have,

Hence the value of x is
(iv) Given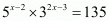
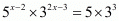
On equating the exponents of 5 and 3 we get,
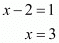
And,
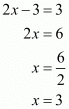
The value of x is
(v) Given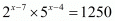
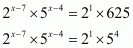
On equating the exponents we get
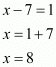
And,
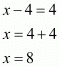
Hence the value of x is
(vi)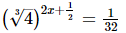
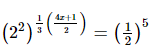
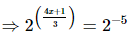
On comparing we get,
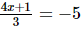
⇒4x+1 = −15
⇒4x = −16
⇒x = −4
(vii) 52x+3=1
52x+3 =50
⇒2x+3 = 0
⇒x = −3/2
(viii) (13)√x = 44 − 34 − 6
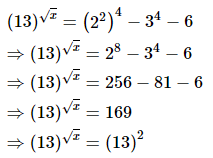
On comparing we get,
√x = 2
on squaring both sides we get,
x = 4
(ix) 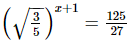
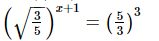
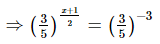
On comparing we get,
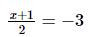
⇒x + 1 = −6
⇒x = −7
Q.7. If 34x = (81)−1 and 101/y = 0.0001, find the value of 2−x+4y.
Proof: It is given that 34x=(81)−1 and 101/y=0.0001.
Now,
34x = (81)−1
⇒34x = (34)−1
⇒(3x)4 = (3−1)4
⇒x = −1
And,
101/y=0.0001
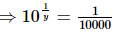
⇒101/y = (1/10)4
⇒101/y = (10)−4
⇒1/y = −4
⇒y = −1/4
Therefore, the value of 2−x+4y is 21+4(−1/4) = 20 = 1
Q.8. If 53x=125 and 10y=0.001, find x and y.
Proof: It is given that 53x = 125 and 10y = 0.001.
Now,
53x = 125
⇒53x = 53
⇒3x = 3
⇒x = 1
And,
10y=0.001
⇒10y = 1/1000
⇒10y = 10−3
⇒y = −3
Hence, the values of x and y are 1 and −3, respectively.
Q.9. Solve the following equations:
(i) 3x+1 = 27×34
(ii)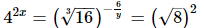
(iii) 3x−1 × 52y−3 = 225
(iv) 8x+1 = 16y+2 and, (1/2)3+x = (1/4)3y
(v) 4x−1 × (0.5)3−2x = (178)x
(vi)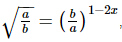 where a and b are distinct primes
where a and b are distinct primes
Proof: (i)
3x+1 = 27×34
⇒3x+1 = 33×34
⇒3x+1 = 33+4
⇒3x+1 = 37
⇒x+1 = 7
⇒x = 6
(ii)
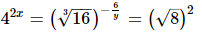
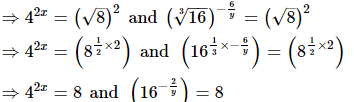
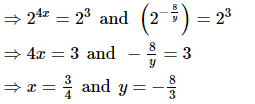
(iii)
3x−1 × 52y−3 = 225
⇒3x−1 × 52y−3 = 3 × 3 × 5 × 5
⇒3x−1 × 52y−3 = 32 × 52
⇒x − 1 = 2 and 2y − 3 = 2
⇒ x = 3 and y = 5/2
(iv)
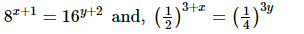
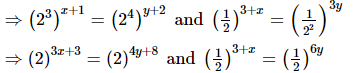
⇒3x+3 = 4y+8 and 3+x = 6y
Now,
3+x = 6y ⇒ x = 6y − 3
Putting x = 6y − 3 in 3x − 4y = 5, we get
3(6y−3)−4y = 5
⇒18y − 9 − 4y = 5
⇒14y = 14
⇒y = 1
Putting y = 1 in x=6y−3, we get
x=6×1−3=3
(v)
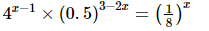
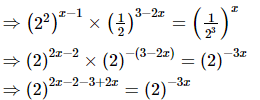
⇒4x − 5 = −3x
⇒7x = 5
⇒x = 5/7
(vi)
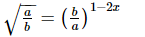
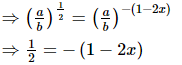
⇒1/2 = 2x − 1
⇒3/2 = 2x
⇒x = 3/4
Q.10. If a and b are distinct primes such that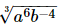 = axb2y, find x and y.
= axb2y, find x and y.
Proof: Given: 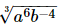 = axb2y
= axb2y
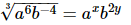
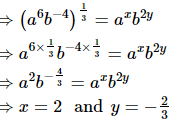
Q.11. If a and b are different positive primes such that
(i)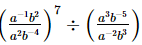 = axby, find x and y.
= axby, find x and y.
(ii)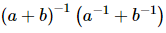 = axby, find x + y + 2.
= axby, find x + y + 2.
Proof: (i)

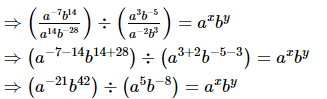
⇒a−21−5b42+8 = axby
⇒a−26b50 = axby
⇒x = −26 and y = 50
(ii)
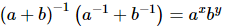
⇒(ab)−1 = axby
⇒a−1b−1 = axby
⇒x=−1 and y=−1
Therefore, the value of x + y + 2 is −1 −1 + 2 = 0.
Q.12. If 2x × 3y × 5z = 2160, find x , y and z. Hence, compute the value of 3x × 2− y × 5− z.
Proof: Given: 2x × 3y × 5z = 2160
First, find out the prime factorization of 2160.
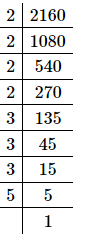
It can be observed that 2160 can be written as 24 × 33 × 51.
Also,
2x × 3y × 5z = 24 × 33 × 51
⇒x = 4, y = 3, z = 1
Therefore, the value of 3x × 2−y × 5−z is 34 × 2−3 × 5−1 = 81 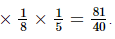
Q.13. If 1176 = 2a × 3b × 7c, find the values of a, b and c. Hence, compute the value of 2a × 3b × 7−c as a fraction.
Proof: First find the prime factorisation of 1176.
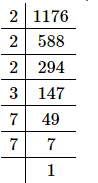
It can be observed that 1176 can be written as 23 × 31 × 72.
1176 = 2a3b7c = 233172
So, a = 3, b = 1 and c = 2.
Therefore, the value of 2a × 3b × 7−c is 23 × 31 × 7−2= 8 x 3 x 1/49 = 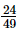
Q.14. Simplify:
(i)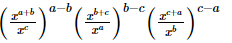
(ii)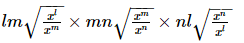
Proof: (i)
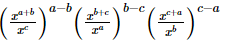
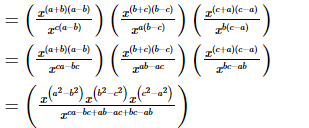
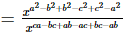
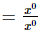
= 1
(ii)
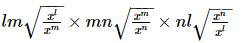
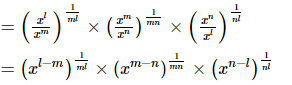
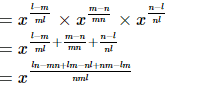
= x0
= 1
Q.15. Show that: 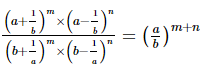
Proof:
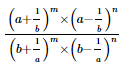
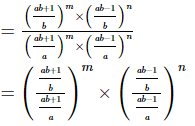
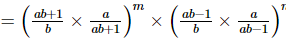
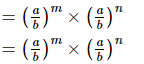
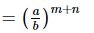
Q.16. (i) If a = xm+nyl, b = xn+lym and c = xl+myn, prove that am−nbn−lcl−m = 1.
(ii) If x = am+n, y = an+l and z = al+m, prove that xmynzl=xnylzm.
Proof: (i) Given: a = xm+nyl, b = xn+lym and c = xl+myn
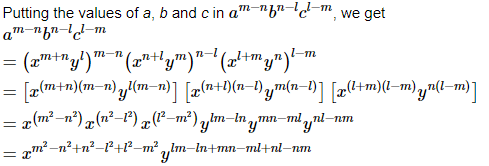
= x0y0
= 1
(ii) Given:x = am+n, y = an+l and z = al+m
Putting the values of x, y and z in xmynzl, we get
xmynzl
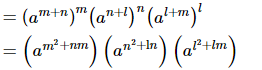
=am2+n2+l2+nm+ln+lm
Putting the values of x, y and z in xnylzm, we get
xnylzm
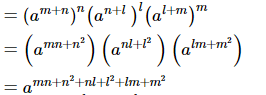
So, xmynzl = xnylzm
Multiple Choice Questions(MCQs)
Q.1. The value of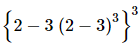 is
is
(a) 5
(b) 125
(c) 1/5
(d) -125
Proof: We have to find the value of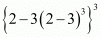
So,
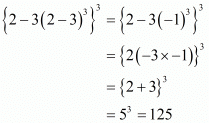
The value of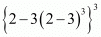 is 125
is 125
Hence the correct choice is
Q.2. The value of x − yx-y when x = 2 and y = −2 is
(a) 18
(b) −18
(c) 14
(d) −14
Proof: Given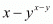
Here x = 2, y = -2
By substituting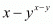 in we get
in we get
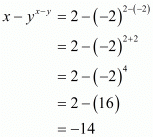
The value of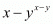 is -14
is -14
Hence the correct choice is
Q.3. The product of the square root of x with the cube root of x is
(a) cube root of the square root of x
(b) sixth root of the fifth power of x
(c) fifth root of the sixth power of x
(d) sixth root of x
Proof: We have to find the product (say L) of the square root of x with the cube root of x is. So,
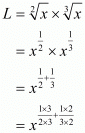
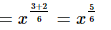
The product of the square root of x with the cube root of x is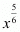
Hence the correct alternative is
Q.4. The seventh root of x divided by the eighth root of x is
(a) x
(b) √x
(c)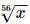
(d)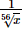
Proof: We have to find he seventh root of x divided by the eighth root of x, so let it be L. So,
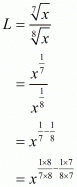
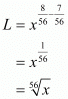
The seventh root of x divided by the eighth root of x is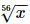
Hence the correct choice is
Q.5. The square root of 64 divided by the cube root of 64 is
(a) 64
(b) 2
(c) 1/2
(d) 642/3
Proof: We have to find the value of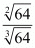
So,
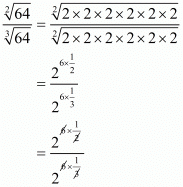
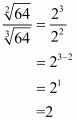
The value of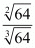 is 2
is 2
Hence the correct choice is
Q.6. Which of the following is (are) not equal to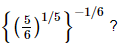
(a)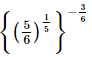
(b)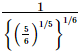
(c)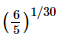
(d)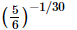
Proof: We have to find the value of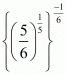
So,
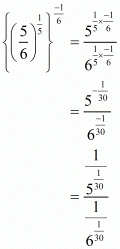
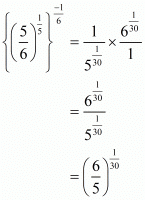
Hence the correct choice is
Q.7. When simplified (x−1+y−1)−1 is equal to
(a) xy
(b) x+y
(c) xy/x+y
(d) x+y/xy
Proof: We have to simplify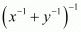
So,
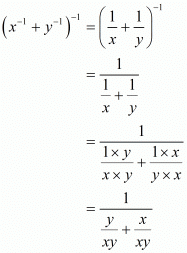
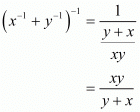
The value of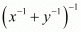 is
is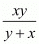
Hence the correct choice is
Q.8. If 8x+1 = 64 , what is the value of 32x+1 ?
(a) 1
(b) 3
(c) 9
(d) 27
Proof: We have to find the value of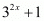 provided
provided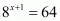
So,
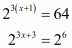
Equating the exponents we get
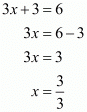
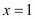
By substitute in we get
we get
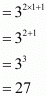
The real value of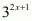 is 27
is 27
Hence the correct choice is
Q.9. If (23)2 = 4x, then 3x =
(a) 3
(b) 6
(c) 9
(d) 27
Proof: We have to find the value of 3x provided(23)2 = 4x
So,
23x2 = 22x
26 = 22x
By equating the exponents we get
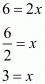
By substituting in 3x we get
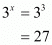
The value of 3x is 27
Hence the correct choice is
Q.10. If x-2 = 64, then x1/3+x0 =
(a) 2
(b) 3
(c) 3/2
(d) 2/3
Proof: We have to find the value of 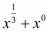 if
if 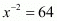
Consider,
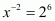
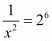
Multiply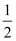 on both sides of powers we get
on both sides of powers we get
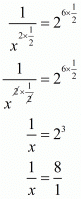
By taking reciprocal on both sides we get,
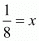
Substituting in
in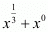 we get,
we get,
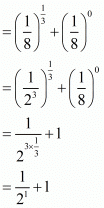
By taking least common multiply we get
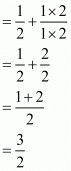
Hence the correct choice is
Q.11. When simplified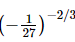 is
is
(a) 9
(b) −9
(c) 1/9
(d) −1/9
Proof: We have to find the value of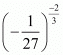
So,
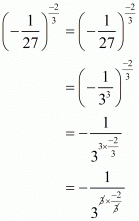
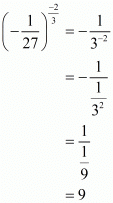
Hence the correct choice is
Q.12. Which one of the following is not equal to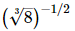 ?
?
(a)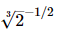
(b)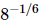
(c)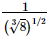
(d)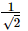
Proof: We have to find the value of
So,
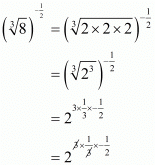
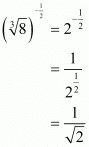
Also,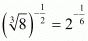
Hence the correct alternative is
Q.13. Which one of the following is not equal to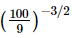 ?
?
(a)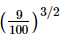
(b)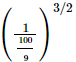
(c)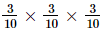
(d)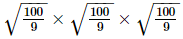
Proof: We have to find the value of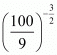
So,
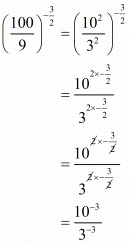
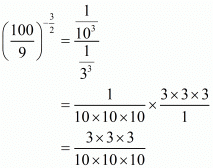
Since,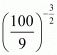 is equal to
is equal to  ,
,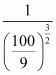 ,
,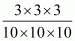
Hence the correct choice is
Q.14. If a, b, c are positive real numbers, then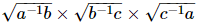 is equal to
is equal to
(a) 1
(b) abc
(c) √abc
(d) 1/abc
Proof: We have to find the value of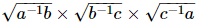 when a, b, c are positive real numbers.
when a, b, c are positive real numbers.
So,
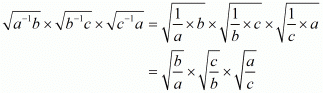
Taking square root as common we get
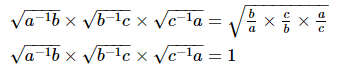
Hence the correct alternative is
Q.15. 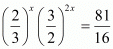 , then x =
, then x =
(a) 2
(b) 3
(c) 4
(d) 1
Proof: We have to find value of x provided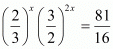
So,
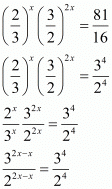
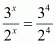
Equating exponents of power we get x = 4
Hence the correct alternative is
Q.16. The value of is
is
(a) 1/2
(b) 2
(c) 1/4
(d) 4
Proof: Find the value of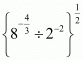
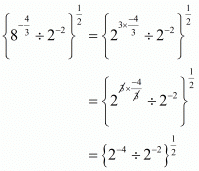
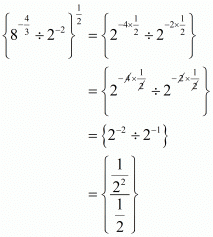
Hence the correct choice is
Q.17. If a, b, c are positive real numbers, then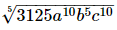 is equal to
is equal to
(a) 5a2bc2
(b) 25ab2c
(c) 5a3bc3
(d) 125a2bc2
Proof: Find value of 
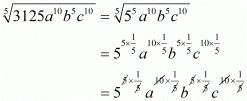
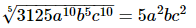
Hence the correct choice is
Q.18. If a, m, n are positive integers, then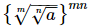 is equal to
is equal to
(a) amn
(b) a
(c) am/n
(d) 1
Proof: Find the value of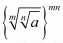
So,
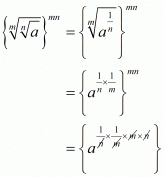
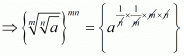
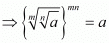
Hence the correct choice is
Q.19. If x = 2 and y = 4, then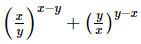 =
=
(a) 4
(b) 8
(c) 12
(d) 2
Proof: We have to find the value of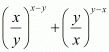
Substitute x = 2, y = 4 in to get
to get
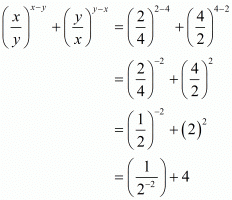
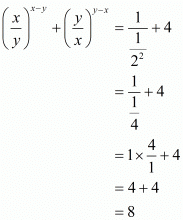
Hence the correct choice is
Q.20. The value of m for which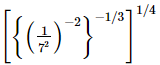 =7m, is
=7m, is
(a) −1/3
(b) 1/4
(c) −3
(d) 2
Proof: We have to find the value of for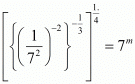
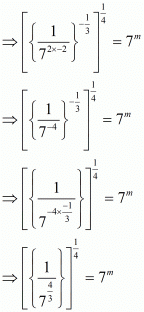
By using rational exponents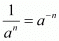
7−1/3=7m
Equating power of exponents we get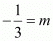
Hence the correct choice is
Q.21. The value of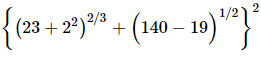 , is
, is
(a) 196
(b) 289
(c) 324
(d) 400
Proof: We have to find the value of 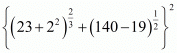
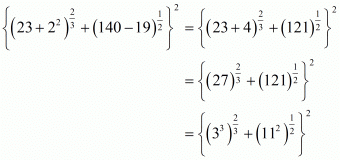
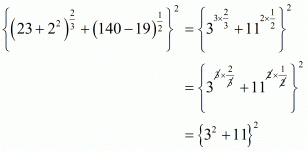
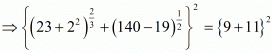
By using the identity we get,
we get,
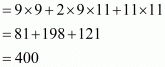
Hence correct choice is
Q.22. (256)0.16 × (256)0.09
(a) 4
(b) 16
(c) 64
(d) 256.25
Proof: We have to find the value of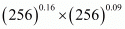
By using law of rational exponents
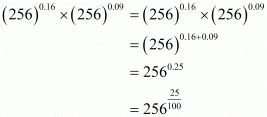
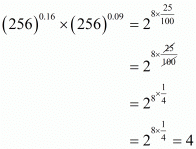
The value of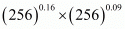 is 4
is 4
Hence the correct choice is
Q.23. If , then 10-y equals
(a) −1/5
(b) 1/50
(c) 1/625
(d) 1/5
Proof: We have to find the value of 10-y
Given that 102y = 25 therefore,
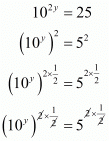
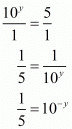
Hence the correct option is .
.
Q.24. If 9x+2 = 240 + 9x, then x = z
(a) 0.5
(b) 0.2
(c) 0.4
(d) 0.1
Proof: We have to find the value of x
Given, 9x+2 = 240 + 9x
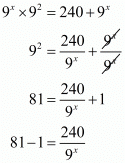
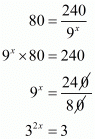
32x = 31
By equating the exponents we get
2x = 1
x = 1/2
x = 0.5
Hence the correct alternative is .
.
Q.25. If x is a positive real number and x2 = 2, then x3 =
(a) √2
(b) 2√2
(c) 3√2
(d) 4
Proof: We have to find x3 provided x2 = 2. So,
By raising both sides to the power 1/2
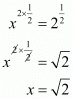
By substituting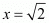 in x3 we get
in x3 we get
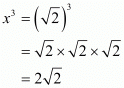
The value of x3 is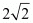
Hence the correct choice is .
.
Q.26. If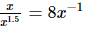 and x > 0, then x =
and x > 0, then x =
(a) √2/4
(b) 2√2
(c) 4
(d) 64
Proof: For , we have to find the value of x
, we have to find the value of x
So,
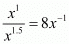
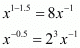
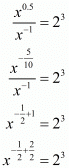
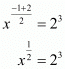
By raising both sides to the power 2 we get
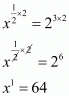
The value of x is 64
Hence the correct alternative is
Q.27. If g = t2/3 + 4t − 1/2, What is the value of g when t = 64?
(a) 21/2
(b) 33/2
(c) 16
(d) 257/16
Proof: Given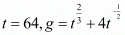 We have to find the value of
We have to find the value of
So,
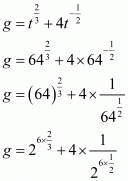
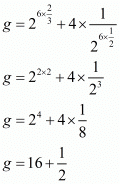
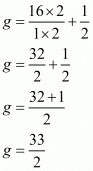
The value of g is 33/2
Hence the correct choice is
Q.28. If 4x − 4x−1 = 24, then (2x)x equals
(a) 5√5
(b) √5
(c) 25√5
(d) 125
Proof: We have to find the value of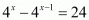
So,
Taking 4x as common factor we get
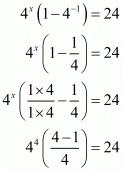
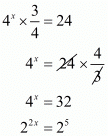
By equating powers of exponents we get
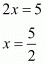
By substituting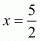 in
in 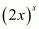 we get
we get
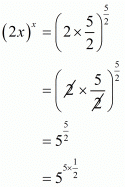
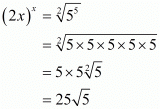
Hence the correct choice is
Q.29. When simplified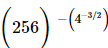 is
is
(a) 8
(b) 1/8
(c) 2
(d) 1/2
Proof: 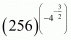
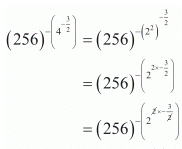

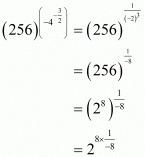
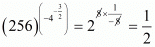
Hence the correct choice is .
.
Q.30. If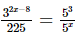 , then x =
, then x =
(a) 2
(b) 3
(c) 5
(d) 4
Proof: We have to find the value of x provided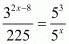
So,
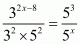
By cross multiplication we get
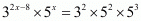
By equating exponents we get
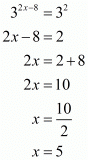
And,
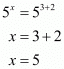
Hence the correct choice is
Q.31. The value of 64-1/3 (641/3-642/3), is
(a) 1
(b) 1/3
(c) −3
(d) −2
Proof: Find the value of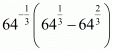
So,

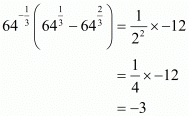
Hence the correct statement is .
.
Q.32. If √5n = 125, then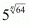 =
=
(a) 25
(b) 1/125
(c) 625
(d) 1/5
Proof: We have to find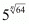 provided
provided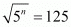
So,
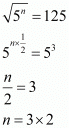
Substitute n = 6 in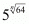 to get
to get
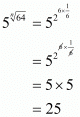
Hence the value of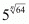 is 25
is 25
The correct choice is
Q.33. If (16)2x+3 =(64)x+3, then 42x-2 =
(a) 64
(b) 256
(c) 32
(d) 512
Proof: We have to find the value of 42x-2 provided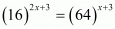
So,
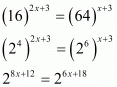
Equating the power of exponents we get
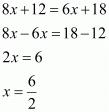
x = 3
The value of 42x-2 is
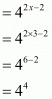
Hence the correct alternative is
Q.34. If 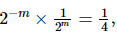 then
then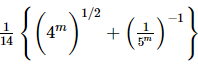 is equal to
is equal to
(a) 1/2
(b) 2
(c) 4
(d) −1/4
Proof: We have to find the value of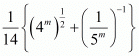 provided
provided 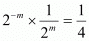
Consider,
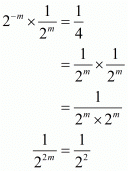
Equating the power of exponents we get
2m = 2
m = 2/2
m = 1
By substituting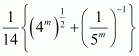 we get
we get
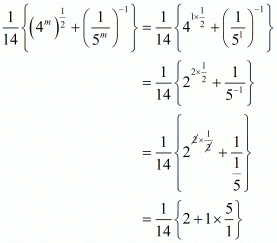
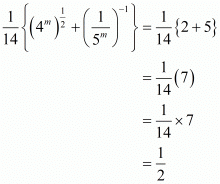
Hence the correct choice is .
.
Q.35. If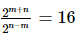 ,
,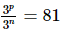 and a = 21/10 , then
and a = 21/10 , then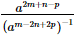 =
=
a) 2
(b) 1/4
(c) 9
(d) 1/8
Proof: Given :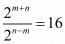 ,
,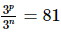 and a = 21/10
and a = 21/10
To find : 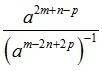
Find :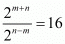
By using rational components We get
We get
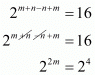
By equating rational exponents we get
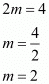
Now,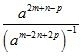 = (a2m+n−p).(am−2n+2p) we get
= (a2m+n−p).(am−2n+2p) we get
=a2m+n−p+m−2n+2p
=a3m−n+p
Now putting value of a = 21/10 we get,
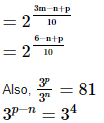
On comparing LHS and RHS we get, p - n = 4.
Now,
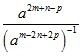 = a3m - n + p
= a3m - n + p
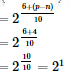
= 2
So, option (a) is the correct answer.
Q.36. If =37 , then x
=37 , then x
(a) 3
(b) −3
(c) 1/3
(d) −1/3
Proof: We have to find the value of x provided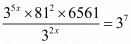
So,
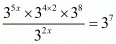
By using law of rational exponents we get
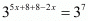
By equating exponents we get
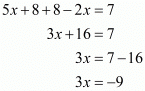
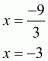
Hence the correct choice is .
.
Q.37. If o <y <x, which statement must be true?
(a) √x−√y = √x−y
(b) √x + √x = √2x
(c) x√y = y√x
(d) √xy = √x√y
Proof: We have to find which statement must be true?
Given 0<y<x,
Option (a) :
Left hand side:
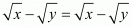
Left hand side is not equal to right hand side
The statement is wrong.
Option (b) :
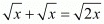
Left hand side:
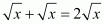
Right Hand side:
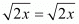
Left hand side is not equal to right hand side
The statement is wrong.
Option (c) :
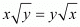
Left hand side:
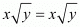
Right Hand side:
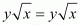
Left hand side is not equal to right hand side
The statement is wrong.
Option (d) :
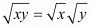
Left hand side:
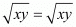
Right Hand side:
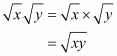
Left hand side is equal to right hand side
The statement is true.
Hence the correct choice is
Q.38. If 10x = 64, what is the value of 10x/2+1 ?
(a) 18
(b) 42
(c) 80
(d) 81
Proof: We have to find the value of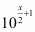 provided
provided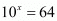
So,
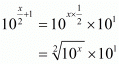
By substituting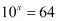 we get
we get
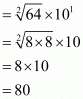
Hence the correct choice is .
.
Q.39. 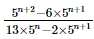 is equal to
is equal to
(a) 5/3
(b) −5/3
(c) 3/5
(d) −3/5
Proof: We have to simplify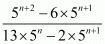
Taking 5n as a common factor we get

Hence the correct alternative is .
.
Q.40. If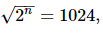 then
then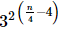 =
=
(a) 3
(b) 9
(c) 27
(d) 81
Proof: We have to find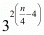
Given
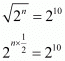
Equating powers of rational exponents we get
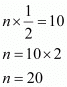
Substituting in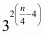 we get
we get
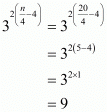
Hence the correct choice is .
.
Fill in the Blanks Types of Questions(FBQs)
Q.1. (212 – 152)2/3 is equal to ________.
Proof: 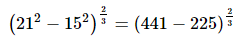

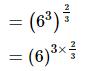
= (6)2
= 36
Hence, (212 – 152)2/3 is equal to 36.
Q.2. 811/4 × 93/2 × 27–4/3 is equal to _________.
Proof: 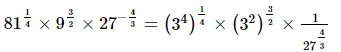

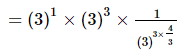
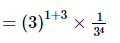

= 1
Hence, 811/4 × 93/2 × 27–4/3 is equal to 1.
Q.3. 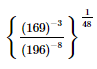 = __________.
= __________.
Proof: 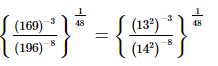
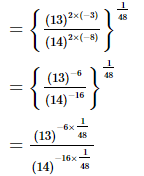
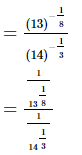
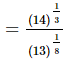
Hence,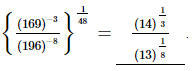
Q.4. If x = 82/3 × 32–2/5, then x–5 = ________.
Proof: Let x = 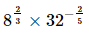
⇒x = 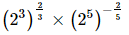
⇒x = 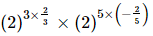
⇒x = 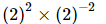
⇒x =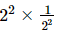
⇒x = 1
Now,
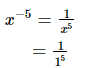
= 1
Hence, if x = 82/3 × 32–2/5, then x–5 = 1.
Q.5. If 6n = 1296, then 6n–3 = _________.
Proof: Let 6n=1296
⇒6n = 64
⇒n = 4
Now,
6n−3=64−3
=61
=6
Hence, if 6n = 1296, then 6n–3 = 6.
Q.6. The value of 4 × (256)–1/4 ÷ (243)1/5 is ________.
Proof: Let x=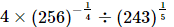
⇒x =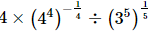
⇒x =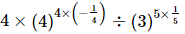
⇒x =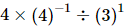
⇒x =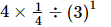
⇒x = 1 ÷ 3
⇒x = 1/3
Hence, the value of 4 × (256)–1/4 ÷ (243)1/5 is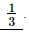
Q.7. If (6x)6=623, then x = ________.
Proof:
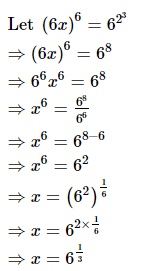
Hence, if
Q.8. 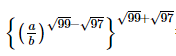 = ___________.
= ___________.
Proof:
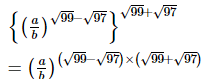
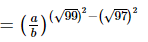 (using the identity: a2−b2=(a+b)(a−b))
(using the identity: a2−b2=(a+b)(a−b))
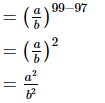
Hence,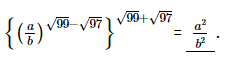
Q.9. 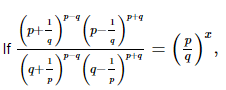 then x =_________.
then x =_________.
Proof:
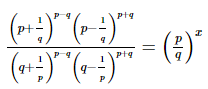
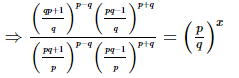
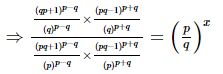
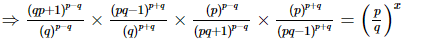
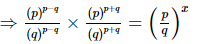
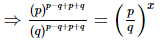
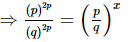
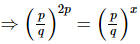
⇒2p = x
⇒x = 2p
Hence, if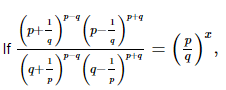 then x=2p.
then x=2p.
Q.10. If 5n+2 = 625, then (12n + 3)1/3 = _________.
Proof: Let 5n+2=625
⇒5n+2 = 54
⇒n+2 =4
⇒n = 2
Now,
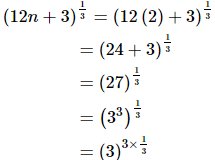
= 3
Hence, if 5n+2 = 625, then (12n + 3)1/3 = 3.
Q.11. If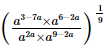 = __________.
= __________.
Proof:
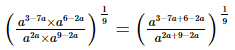

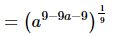
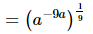
=(a)−a
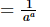
Hence,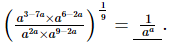
Q.12. If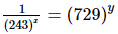 =33 , then 5x + 6y = __________.
=33 , then 5x + 6y = __________.
Proof: Given: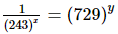 =33
=33
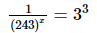
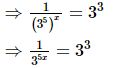
⇒3−5x = 33
⇒−5x = 3
⇒5x = −3 ...(1)
(729)y = 33
⇒(36)y = 33
⇒36y = 33
⇒6y = 3 ...(2)
Adding (1) and (2), we get
5x + 6y=−3 + 3
=0
Hence, 5x + 6y = 0.
Q.13. If 6x–y = 36 and 3x+y = 729, then x2 – y2 = _________.
Proof: Given: 6x−y = 36
and 3x+y = 729
6x−y = 36
⇒ 6x−y = 62
⇒x−y = 2 ...(1)
3x+y = 729
⇒3x+y = 36
⇒x+y = 6 ...(2)
Adding (1) and (2), we get
2x = 8
⇒x = 4
Substituting the value of x in (2), we get
4+y = 6
⇒y = 2
Now,
x2−y2 = 42−22
=16 − 4
=12
Hence, x2 – y2 = 12.
Q.14. 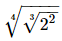 equals __________.
equals __________.
Proof:
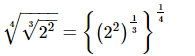
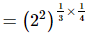
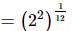
=(2)1/6
Hence,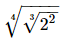 equals
equals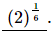
Q.15. The product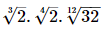 is equal to ________.
is equal to ________.
Proof: 
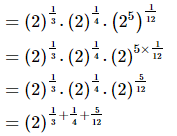
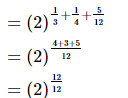
= (2)1
= 2
Hence, the product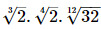 is equal to 2.
is equal to 2.
Q.16.  is equal to _________.
is equal to _________.
Proof: 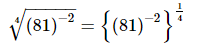
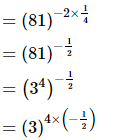
= (3)−2
= 1/32
= 1/9
Hence, is equal to
is equal to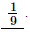
Q.17. The value of (256)0.16 × (256)0.09 is ________.
Proof: (256)0.16 × (256)0.09 = (256)0.16+0.09
= (256)0.25
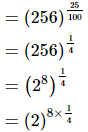
= (2)2
= 4
Hence, the value of (256)0.16 × (256)0.09 is 4.
Very Short Answer Type Questions(VSAQs)
Q.1. Write (625)−1/4 in decimal form.
Proof: We have to write (625)−1/4 in decimal form. So,
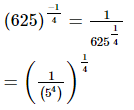
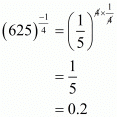
Hence the decimal form of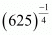 is
is 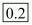
Q.2. State the product law of exponents.
Proof:
State the product law of exponents.
If is any real number and m ,n are positive integers, then
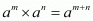
By definition, we have
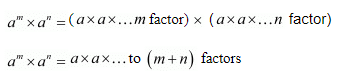
am x an = am+n
Thus the exponent "product rule" tells us that, when multiplying two powers that have the same base, we can add the exponents.
Q.3. State the quotient law of exponents.
Proof: The quotient rule tells us that we can divide two powers with the same base by subtracting the exponents. If a is a non-zero real number and m, n are positive integers, then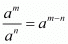
We shall divide the proof into three parts
(i) when m > n
(ii) when m = n
(iii) when m < n
Case 1
when m > n
We have
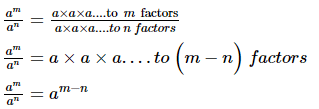
Case 2
when m = n
We get

Cancelling common factors in numerator and denominator we get,
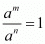
By definition we can write 1 as a0
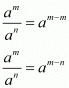
Case 3
when m < n
In this case, we have
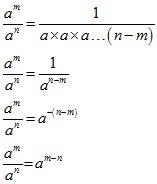
Hence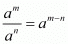 , whether m > n,m = n or, m < n
, whether m > n,m = n or, m < n
Q.4. State the power law of exponents.
Proof: The "power rule" tell us that to raise a power to a power, just multiply the exponents.
If a is any real number and m, n are positive integers, then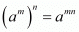
We have,
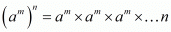 factors
factors
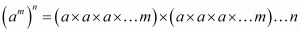 factors
factors
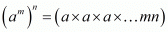
Hence,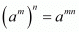
Q.5. If 24 × 42 =16x, then find the value of x.
Proof: We have to find the value of x provided 24 × 42 =16x
So,
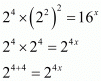
By equating the exponents we get
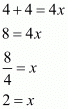
Hence the value of x is  .
.
Q.6. If 3x-1 = 9 and 4y+2 = 64, what is the value of x/y ?
Proof: We have to find the value of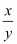 for
for 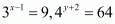
So,
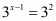
By equating the exponent we get
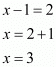
Let’s take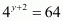
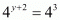
By equating the exponent we get
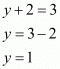
By substituting x = 3, y = 1 we get 3 / 1
Hence the value of x/y is 3.
Q.7. Write the value of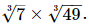
Proof: We have to find the value of 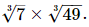 So,
So,

By using law rational exponents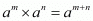 we get
we get
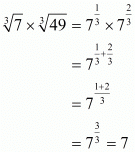
Hence the value of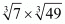 is
is 
Q.8. Write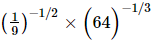 as a rational number.
as a rational number.
Proof: We have to find the value of 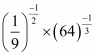
So,
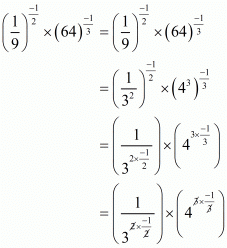
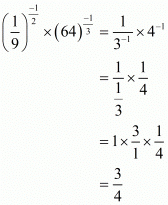
Hence the value of the value of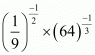 is
is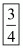 .
.
Q.9. Write the value of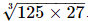
Proof: We have to find the value of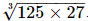 So,
So,
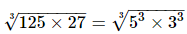 = = 5×3 =15
= = 5×3 =15
Hence the value of the value of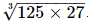 is
is
Q.10. For any positive real number x, find the value of
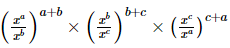
Proof: We have to find the value of L = 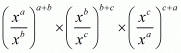
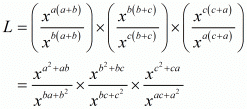
By using rational exponents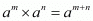 we get
we get
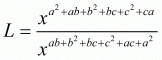
By using rational exponents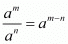 we get
we get
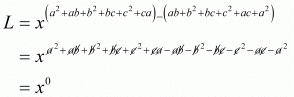
By definition we can write x0 as 1
Hence the value of expression is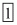 .
.
Q.11. Write the value of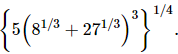
Proof: We have to find the value of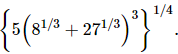 So,
So,

By using rational exponents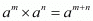 we get
we get
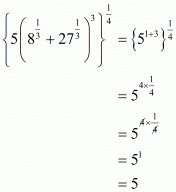
Hence the simplified value of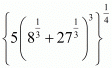 is
is .
.
Q.12. Simplify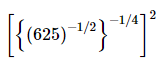
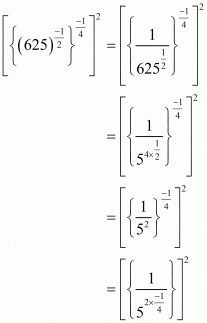
Proof: We have to simplify So,
So,
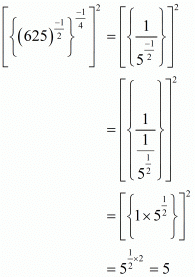
Hence, the value of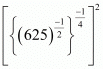 is
is  .
.
Q.13. For any positive real number x, write the value of
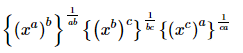
Proof: We have to simplify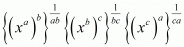 So,
So,

By using rational exponents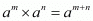 , we get
, we get
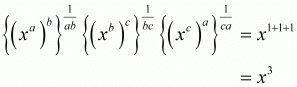
Hence the value of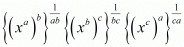 is x3.
is x3.
Q.14. If (x − 1)3 = 8, What is the value of (x + 1)2 ?
Proof: We have to find the value of (x + 1)2, where (x − 1)3 = 8
Consider (x − 1)3 =23
By equating the base, we get
x - 2 = 1
x = 2 + 1
x = 3
By substituting x = 3 in (x + 1)2
= (x + 1)2
= (3 + 1)2is
= 42
= 16
Hence the value of(x + 1)2 is 16.
|
40 videos|471 docs|57 tests
|
FAQs on Exponents of Real Numbers- 2 RD Sharma Solutions - Mathematics (Maths) Class 9
| 1. What are exponents of real numbers? |  |
| 2. How do you simplify expressions with exponents? |  |
| 3. What is the meaning of a negative exponent? |  |
| 4. Can exponents be applied to any real number? |  |
| 5. How are exponents used in real-life situations? |  |
















