Number System- 5 RD Sharma Solutions | Extra Documents & Tests for Class 9 PDF Download

Q.1. Complete the following sentences:

(i) Every point on the number line corresponds to a .... number which many be either ... or ...

(ii) The decimal form of an irrational number is neither ... nor ...

(iii) The decimal representation of a rational number is either ... or ...

(iv) Every real number is either ... number or ... number.

Proof: (i) Every point on the number line corresponds to a real number which may be either rational or an irrational number.

(ii) The decimal form of an irrational number is neither terminating nor repeating.

(iii) The decimal representation of rational number is either terminating, recurring.

(iv) Every real number is either rational number or an irrational number because rational or an irrational number is a family of real number.

Q.2. Find whether the following statement are true or false.

(i) Every real number is either rational or irrational.

(ii) π is an irrational number.

(iii) Irrational numbers cannot be represented by points on the number line.

Proof: (i) True, because rational or an irrational number is a family of real number. So every real number is either rational or an irrational number.

(ii) True, because the decimal representation of an irrational is always non-terminating or non-repeating. So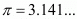is an irrational number.

(iii) False, because we can represent irrational numbers by points on the number line.

Q.3. Represent √6, √7, √8 on the number line.

Proof: We are asked to represent √6, √7, √8 on the number line

We will follow certain algorithm to represent these numbers on real line

We will consider point A as reference point to measure the distance

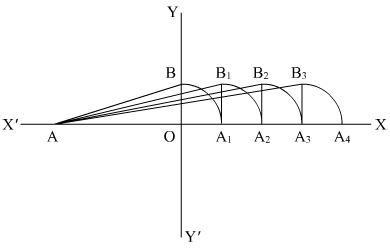
(1) First of all draw a line AX and YY’ perpendicular to AX

(2) Consider AO = 2 units and OB = 1 unit, so

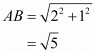
(3) Take A as center and AB as radius, draw an arc which cuts line AX at A1

(4) Draw a perpendicular line A1B1 to AX such that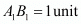and

(5) Take A as center and AB1 as radius and draw an arc which cuts the line AX at A2.

Here 

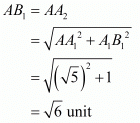
SoAA₂ = √6 unit

So A₂ is the representation for √6

(1) Draw line A₂B₂ perpendicular to AX

(2) Take A center and AB₂ as radius and draw an arc which cuts the horizontal line at A₃ such that

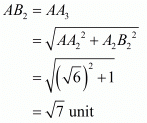
So point A₃ is the representation of √7

(3) Again draw the perpendicular line A₃B₃ to AX

(4) Take A as center and AB₃ as radius and draw an arc which cuts the horizontal line at A₄

Here;

A₄ is basically the representation of √8

Q.4. Represent √3.5, √9.4, √10.5 on the real number line.

Proof:  We are asked to represent the real numbers √3.5, √9.4, √10.5 on the real number line

We will follow a certain algorithm to represent these numbers on real number line

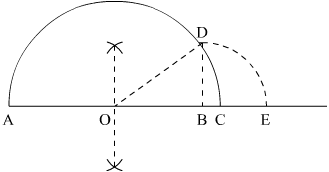
(a) √3.5

We will take A as reference point to measure the distance

(1) Draw a sufficiently large line and mark a point A on it

(2) Take a point B on the line such that AB = 3.5 cm

(3) Mark a point C on the line such that BC = 1 cm

(4) Find mid point of AB and let it be O

(5) Take O as center and OC as radius and draw a semi circle. Draw a perpendicular BD which cuts the semi circle at D

(6) Take B as the center and BD as radius, draw an arc which cuts the horizontal line at E 

(7) Point E is the representation of √3.5

(b) √9.4

We will take A as reference point to measure the distance. We will follow the same figure in the part (a) 

(1) Draw a sufficiently large line and mark a point A on it

(2) Take a point B on the line such that AB = 9.4 cm

(3) Mark a point C on the line such that BC = 1 cm

(4) Find mid point of AB and let it be O

(5) Take O as center and OC as radius and draw a semi circle. Draw a perpendicular BC which cuts the semi circle at D

(6) Take B as the center and BD as radius, draw an arc which cuts the horizontal line at E 

(7) Point E is the representation of √9.4

(c) √10.5

We will take A as reference point to measure the distance. We will follow the same figure in the part (a) 

(1) Draw a sufficiently large line and mark a point A on 

(2) Take a point B on the line such that AB = 10.5 cm

(3) Mark a point C on the line such that BC = 1 cm

(4) Find mid point of AB and let it be O

(5) Take O as center and OC as radius and draw a semi circle. Draw a perpendicular BC which cuts the semi circle at D

(6) Take B as the center and BD as radius, draw an arc which cuts the horizontal line at E 

(7) Point E is the representation of √10.5