Number System- 6 RD Sharma Solutions | Extra Documents & Tests for Class 9 PDF Download

Q.1. Visualize 2.665 on the number line, using successive magnification.

Proof:

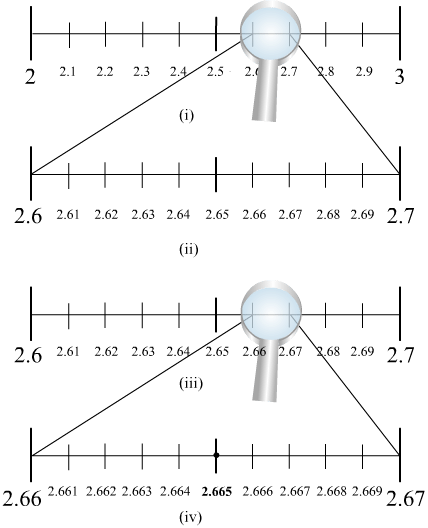
We know that 2.665 lies between 2 and 3. So, we divide the number line into 10 equal parts and mark each point of division. The first mark on the right of 2 will be 2.1 followed by 2.2 and so on. The point left of 3 will be 2.9. Now, the magnified view of this will show that 2.665 lies between 2.6 and 2.7. So, our focus will be now 2.6 and 2.7. We divide this again into 10 equal parts. The first part will be 2.61 followed by 2.62 and so on. 

We now magnify this again and find that 2.665 lies between 2.66 and 2.67. So, we magnify this portion and divide it again into 10 equal parts. The first part will represent 2.661, next will be 2.662 and so on. So, 2.665 will be 5th mark in this subdivision as shown in the figure.

Q.2. Visualize the representation of 5.37¯ on the number line up to 5 decimal places, that is up to 5.37777.

Proof: 

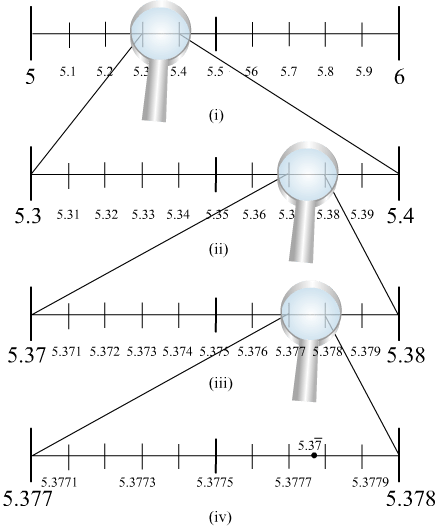
We know that 5.37¯ will lie between 5 and 6. So, we locate 5.37¯ between 5 and 6. We divide this portion of the number line between 5 and 6 into 10 equal parts and use a magnifying glass to visualize 5.37¯ . 

5.37¯ lies between 5.37 and 5.38. To visualize 5.37¯ more accurately we use a magnifying glass to visualize between 5.377 and 5.378. Again, we divide the portion between 5.377 and 5.378 into 10 equal parts and visualize more closely to represent 5.37¯ as given in the figure. This is located between 5.3778 and 5.3777. 

MULTIPLE CHOICE QUESTIONS(MCQs)

Q.1. Mark the correct alternative in each of the following:

1. Which one of the following is a correct statement?

(a) Decimal expansion of a rational number is terminating

(b) Decimal expansion of a rational number is non-terminating

(c) Decimal expansion of an irrational number is terminating

(d) Decimal expansion of an irrational number is non-terminating and non-repeating

Proof: The decimal expansion of an irrational number is non-terminating and non- repeating. Thus, we can say that a number, whose decimal expansion is non-terminating and non- repeating, called irrational number. And the decimal expansion of rational number is either terminating or repeating. Thus, we can say that a number, whose decimal expansion is either terminating or repeating, is called a rational number.

Hence the correct option is.

Q.2. Which one of the following statements is true?

(a) The sum of two irrational numbers is always an irrational number

(b) The sum of two irrational numbers is always a rational number

(c) The sum of two irrational numbers may be a rational number or an irrational number

(d) The sum of two irrational numbers is always an integer

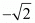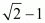Proof: Since,andare two irrational number and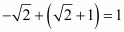

Therefore, sum of two irrational numbers may be rational

Now, let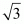and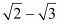be two irrational numbers and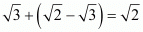

Therefore, sum of two irrational number may be irrational

Hence the correct option is.

Q.3. Which of the following is a correct statement?

(a) Sum of two irrational numbers is always irrational

(b) Sum of a rational and irrational number is always an irrational number

(c) Square of an irrational number is always a rational number

(d) Sum of two rational numbers can never be an integer

Proof: The sum of irrational number and rational number is always irrational number.

Let a be a rational number and b be an irrational number.

Then, 

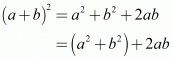
As 2ab is irrational therefore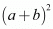is irrational.

Hence (a + b) is irrational.

Therefore answer is.

Q.4. Which of the following statements is true?

(a) Product of two irrational numbers is always irrational

(b) Product of a rational and an irrational number is always irrational

(c) Sum of two irrational numbers can never be irrational

(d) Sum of an integer and a rational number can never be an integer

Proof: Since we know that the product of rational and irrational number is always an irrational. For example: Let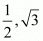are rational and irrational numbers respectively and their product is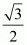

Hence the correct option is.

Q.5. Which of the following is irrational?

(a) √4 / 9

(b) √4 / 5

(c) √7

(d) √81

Proof: Given that

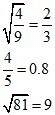
And 7 is not a perfect square.

Hence the correct option is.

Q.6. Which of the following is irrational?

(i) 0.14

(ii)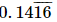

(iii)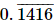

(iv) 0.1014001400014...

Proof:  Given that

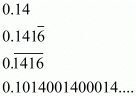
Here 0.1014001400014...is non-terminating or non-repeating. So it is an irrational number.

Hence the correct option is.

Q.7. Which of the following is rational?

(a) √3

(b) π

(c) 4/0

(d) 0/4

Proof: Given that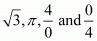

Here,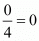, this is the form of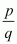So this is a rational number

Hence the correct option is.

Q.8. The number 0.318564318564318564 ........ is:

(a) a natural number

(b) an integer

(c) a rational number

(d) an irrational number

Proof: Since the given number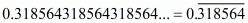is repeating, so it is rational number because rational number is always either terminating or repeating 

Hence the correct option is.

Q.9. If n is a natural number, then √n is

(a) always a natural number

(b) always an irrational number

(c) always an irrational number

(d) sometimes a natural number and sometimes an irrational number

Proof: The term “natural number” refers either to a member of the set of positive integer 1,2,3.

And natural number starts from one of counting digit .Thus, if n is a natural number then sometimes n is a perfect square and sometimes it is not.

Therefore, sometimes √n is a natural number and sometimes it is an irrational number

Hence the correct option is.

Q.10. Which of the following numbers can be represented as non-terminating, repeating decimals?

(a) 39/24

(b) 3/16

(c) 3/11

(d) 137/25

Proof: Given that

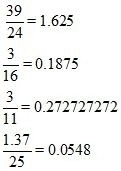
Here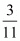is repeating but non-terminating.

Hence the correct option is.

Q.11. Every point on a number line represents

(a) a unique real number

(b) a natural number

(c) a rational number

(d) an irrational number

Proof: 

In basic mathematics, number line is a picture of straight line on which every point is assumed to correspond to real number.

Hence the correct option is.

Q.12. Which of the following is irrational?

(a) 0.15

(b) 0.01516

(c)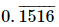

(d) 0.5015001500015.

Proof: Given decimal numbers are

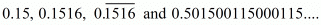
Here the number 0.5015001500015... is non terminating or non-repeating.

Hence the correct option is.

Q.13. The number 0.3¯ in the form p/q, where p and q are integers and q ≠ 0, is

(a) 33/100

(b) 3/10

(c) 1/3

(d) 3/100

Proof: Given number is 0.3¯

The correct option is

Q.14. 0.32¯  when expressed in the form p/q (p, q are integers q ≠ 0), is

(a) 8/25

(b) 29/90

(c) 32/99

(d) 32/199

Proof: Given that 0.32¯

Now we have to express this number into p/q form

Let X =0.32¯

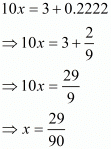
The correct option is

Q.15. 23.43¯ when expressed in the form p/q (p, q are integers q ≠ 0), is

(a)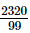

(b)

(c)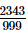

(d)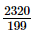

Proof: Given that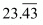

Now we have to express this number into the form of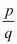

Let

x = 23.43

x = 23+0.4343...

x = 23+43 / 99

x=2277+43 / 99

=2320 / 99

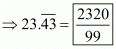
The correct option is

Q.16. 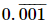when expressed in the form p/q (p, q are integers, q ≠ 0), is

(a)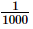

(b)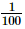

(c)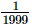

(d)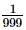

Proof: Given that

Now we have to express this number into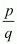from

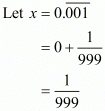
The correct option is

Q.17. The value of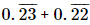is

(a)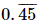

(b)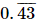

(c)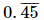

(d) 0.45

Proof:  Given that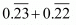

Let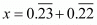

Now we have to find the value of x

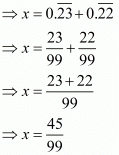
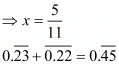
The correct option is

Q.18. An irrational number between 2 and 2.5 is

(a) √11

(b) √5

(c) √22.5

(d) √12.5

Proof: Let 

a = 2

b = 2.5

Here a and b are rational numbers. So we observe that in first decimal place a and b have distinct. According to question a < b.so an irrational number between 2 and 2.5 is 2.236067978 OR √5.

Hence the correct answer is

Q.19. The number of consecutive zeros in 2³ ×3⁴ ×5⁴ ×7, is

(a) 3

(b) 2

(c) 4

(d) 5

Proof: We are given the following expression and asked to find out the number of consecutive zeros

2³ ×3⁴ ×5⁴ ×7

We basically, will focus on the powers of 2 and 5 because the multiplication of these two number gives one zero. So

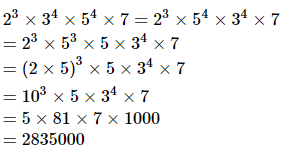
Therefore the consecutive zeros at the last is 3

So the option (a) is correct

Q.20. The smallest rational number by which 1/3 should be multiplied so that its decimal expansion terminates after one place of decimal, is

(a) 1/10

(b) 3/10

(c)  3

(d) 30

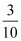Proof: Give number isNow multiplying byin the given number, we have

Hence the correct option is

Fill in the Blanks Types Questions(FBQs)

Q.1. The decimal expansion of a rational number is either ______ or _______.

Proof: The decimal expansion of a rational number either terminates after finitely many digits or ends with a repeating sequence.

Hence, the decimal expansion of a rational number is either terminating or recurring.

Q.2. The decimal expansion of an irrational number is non-terminating and _______.

Proof: The decimal expansion of a rational number either terminates after finitely many digits or ends with a repeating sequence.

In case of irrational number, the decimal expansion neither terminates nor repeats after finitely many digits.

Hence, the decimal expansion of an irrational number is non-terminating and non-repeating.

Q.3. The decimal expansion of √2 is _______ and  _________.

Proof:  √2  is an irrational number.

The decimal expansion of an irrational number neither terminates nor repeats after finitely many digits.

Hence, the decimal expansion of √2 is non-terminating and non-repeating.

Q.4. The value of 1.999. in the form of m/n, where m and n are integers and n ≠ 0, is _______.

Proof: Let x=1.999.....                ...(1)

Multiply (1) by 10 on both sides, we get

10x=19.999.....                ...(2)

Subtracting (1) from (2), we get

10x−x=19.999....−1.999....

⇒9x=18

⇒x=18/9

⇒x=2/1

Hence, the value of 1.999... in the form of m/n, where m and n are integers and n ≠ 0, is 2/1.

Q.5. Every recurring decimal is a _________ number.

Proof: The decimal expansion of a rational number either terminates after finitely many digits or ends with a repeating sequence.

Hence, every recurring decimal is a rational number.

Q.6. π is an _______ number.

Proof: The decimal expansion of π neither terminates nor repeats after finitely many digits.

Therefore, it is an irrational number.

Hence, π is an irrational number.

Q.7. The product of a non-zero rational number with an irrational number is always an ________ number.

Proof: The product of a non-zero rational number with an irrational number always results in an irrational number.

Hence, the product of a non-zero rational number with an irrational number is always an irrational number.

Q.8. The simplest form of  is _______.

Proof: Let x=1.6666.....                ...(1)
Multiply (1) by 10 on both sides, we get

10x=16.6666.....                ...(2)

Subtracting (1) from (2), we get

10x−x=16.6666....−1.6666....

⇒9x=15

⇒x=15/9

⇒x=5/3

Hence, the simplest form of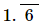 is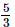

Q.9. 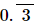+ 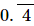 is equal to _________.

Proof:  Let x=0.3333.....                ...(1)

Multiply (1) by 10 on both sides, we get

10x=3.3333.....                  ...(2)

Subtracting (1) from (2), we get

10x−x=3.333....−0.333....

⇒9x=3

⇒x=3/9                              ...(3)

Let y=0.4444.....                ...(4)

Multiply (1) by 10 on both sides, we get

10y=4.4444.....                  ...(5)

Subtracting (4) from (5), we get

10y−y=4.4444....−0.4444....

⇒9y=4

⇒y=4/9                              ...(6)

Now, 0.3+0.4 = x+y             

=3/9+4/9            (From (3) and (6))             

=

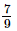
Hence,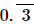 +  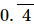is equal to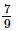 

Q.10. The sum of a rational number and an irrational number is ________ number.

Proof: The sum of a rational number and an irrational number always results in an irrational number.

Hence, the sum of a rational number and an irrational number is an irrational number.

Q.11. Every real number is either ________ or _______ number.

Proof: The real number includes all the rational as well as irrational numbers.

Hence, every real number is either rational or irrational number.