Class 8 Exam > Class 8 Notes > RD Sharma Solutions for Class 8 Mathematics > RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3)
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Write the possible unit's digits of the square root of the following numbers. Which of these numbers are odd square roots?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
Answer 1: (i) The unit digit of the number 9801 is 1. So, the possible unit digits are 1 or 9 (Table 3.4). Note that 9801 is equal to 992. Hence, the square root is an odd number.
(ii) The unit digit of the number 99856 is 6. So, the possible unit digits are 4 or 6 (Table 3.4). Since its last digit is 6 (an even number), it cannot have an odd number as its square root.
(iii) The unit digit of the number 998001 is 1. So, the possible unit digits are 1 or 9. Note that 998001 is equal to (33 x 37)2. Hence, the square root is an odd number.
(iv) The unit digit of the number 657666025 is 5. So, the only possible unit digit is 5. Note that 657666025 is equal to (5 x 23 x 223)2. Hence, the square root is an odd number.
Hence, among the given numbers, (i), (iii) and (iv) have odd numbers as their square roots.
Question 2: Find the square root of each of the following by prime factorization.
(i) 441
(ii) 196
(iii) 529
(iv) 1764
(v) 1156
(vi) 4096
(vii) 7056
(viii) 8281
(ix) 11664
(x) 47089
(xi) 24336
(xii) 190969
(xiii) 586756
(xiv) 27225
(xv) 3013696
Answer 2: (i) Resolving 441 into prime factors:
441 = 3 x 3 x 7 x 7
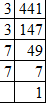
Grouping the factors into pairs of equal factors:
441 = (3 x 3) x (7 x 7)
Taking one factor for each pair, we get the square root of 441:
3 x 7 = 21
(ii) Resolving 196 into prime factors:
196 = 2 x 2 x 7 x 7
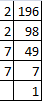
Grouping the factors into pairs of equal factors:
196 = (2 x 2) x (7 x 7)
Taking one factor for each pair, we get the square root of 196:
2 x 7 = 14
(iii) Resolving 529 into prime factors:
529 = 23 x 23
Grouping the factors into pairs of equal factors:
529= (23 x 23)
Taking one factor for each pair, we get the square root of 529 as 23.
(iv) Resolving 1764 into prime factors:
1764 = 2 x 2 x 3 x 3 x 7 x 7
Grouping the factors into pairs of equal factors:
1764 = (2 x 2) x (3 x 3) x (7 x 7)
Taking one factor for each pair, we get the square root of 1764:
2 x 3 x 7 = 42
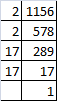
(v) Resolving 1156 into prime factors:
1156 = 2 x 2 x 17 x 17
Grouping the factors into pairs of equal factors:
1156 = (2 x 2) x (17 x 17)
Taking one factor for each pair, we get the square root of 1156:
2 x 17 = 34
(vi) Resolving 4096 into prime factors:
4096 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
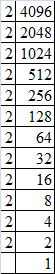
Grouping the factors into pairs of equal factors:
4096 = (2 x 2) x (2 x 2) x (2 x 2) x (2 x 2) x (2 x 2) x (2 x 2)
Taking one factor for each pair, we get the square root of 4096:
(2 x 2) x (2 x 2) x (2 x 2) = 64
(vii) Resolving 7056 into prime factors:
7056 = 2 x 2 x 2 x 2 x 3 x 3 x 7 x 7
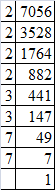
Grouping the factors into pairs of equal factors:
7056 = (2 x 2) x (2 x 2) x (3 x 3) x (7 x 7)
Taking one factor for each pair, we get the square root of 705:
2 x 2 x 3 x 7 = 84
(viii) Resolving 8281 into prime factors:
8281 = 7 x 7 x 13 x 13
Grouping the factors into pairs of equal factors:
8281 = (7 x 7) x (13 x 13)
Taking one factor for each pair, we get the square root of 8281:
7 x 13 = 91
(ix) Resolving 11664 into prime factors:
11664 = 2 x 2 x 2 x 2 x 3 x 3 x 3 x 3 x 3 x 3
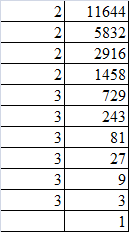
Grouping the factors into pairs of equal factors:
11664 = (2 x 2) x (2 x 2) x (3 x 3) x (3 x 3) x (3 x 3)
Taking one factor for each pair, we get the square root of 11664:
2 x 2 x 3 x 3 x 3 = 108
(x) Resolving 47089 into prime factors:
47089 = 7 x 7 x 31 x 31
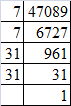
Grouping the factors into pairs of equal factors:
47089 = (7 x 7) x (31 x 31)
Taking one factor for each pair, we get the square root of 47089:
7 x 31 = 217
(xi) Resolving 24336 into prime factors:
24336 = 2 x 2 x 2 x 2 x 3 x 3 x 13 x 13
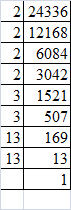
Grouping the factors into pairs of equal factors:
24336 = (2 x 2) x (2 x 2) x (3 x 3) x (13 x 13)
Taking one factor for each pair, we get the square root of 24336:
2 x 2 x 3 x 13 = 156
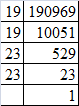
(xii) Resolving 190969 into prime factors:
190969 = 19 x 19 x 23 x 23
Grouping the factors into pairs of equal factors:
190969 = (19 x 19) x (23 x 23)
Taking one factor for each pair, we get the square root of 190969:
19 x 23 = 437
(xiii) Resolving 586756 into prime factors:
586756 = 2 x 2 x 383 x 383
Grouping the factors into pairs of equal factors:
586756 = (2 x 2) x (383 x 383)
Taking one factor for each pair, we get the square root of 586756:
2 x 383 = 766
(xiv) Resolving 27225 into prime factors:
27225 = 3 x 3 x 5 x 5 x 11 x 11
Grouping the factors into pairs of equal factors:
27225 = (3 x 3) x (5 x 5) x (11 x 11)
Taking one factor for each pair, we get the square root of 27225:
3 x 5 x 11 = 165
(xv) Resolving 3013696 into prime factors:
3013696 = 2 x 2 x 2 x 2 x 2 x 2 x 7 x 7 x 31 x 31
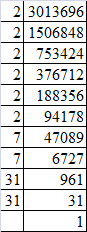
Grouping the factors into pairs of equal factors:
3013696 = (2 x 2) x (2 x 2) x (2 x 2) x (7 x 7) x (31 x 31)
Taking one factor for each pair, we get the square root of 3013696:
2 x 2 x 2 x 7 x 31 = 1736
Question 3: Find the smallest number by which 180 must be multiplied so that it becomes a perfect square. Also, find the square root of the perfect square so obtained.
Answer 3: The prime factorisation of 180:
180 = 2 x 2 x 3 x 3 x 5
Grouping the factors into pairs of equal factors, we get:
180 = (2 x 2) x (3 x 3) x 5
The factor, 5 does not have a pair. Therefore, we must multiply 180 by 5 to make a perfect square. The new number is:
(2 x 2) x (3 x 3) x (5 x 5) = 900
Taking one factor from each pair on the LHS, the square root of the new number is 2 x 3 x 5, which is equal to 30.
Question 4: Find the smallest number by which 147 must be multiplied so that it becomes a perfect square. Also, find the square root of the number so obtained.
Answer 4: The prime factorisation of 147:
147 = 3 x 7 x 7
Grouping the factors into pairs of equal factors, we get:
147 = 3 x (7 x 7)
The factor, 3 does not have a pair. Therefore, we must multiply 147 by 3 to make a perfect square. The new number is:
(3 x 3) x (7 x 7) = 441
Taking one factor from each pair on the LHS, the square root of the new number is 3 x 7, which is equal to 21.
Question 5: Find the smallest number by which 3645 must be divided so that it becomes a perfect square. Also, find the square root of the resulting number.
Answer 5: The prime factorisation of 3645:
3645 = 3 x 3 x 3 x 3 x 3 x 3 x 5
Grouping the factors into pairs of equal factors, we get:
3645 = (3 x 3) x (3 x 3) x (3 x 3) x 5
The factor, 5 does not have a pair. Therefore, we must divide 3645 by 5 to make a perfect square. The new number is:
(3 x 3) x (3 x 3) x (3 x 3) = 729
Taking one factor from each pair on the LHS, the square root of the new number is 3 x 3 x 3, which is equal to 27.
Question 6: Find the smallest number by which 1152 must be divided so that it becomes a perfect square. Also, find the square root of the number so obtained.
Answer 6: The prime factorisation of 1152:
1152 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3
Grouping the factors into pairs of equal factors, we get:
1152 = (2 x 2) x (2 x 2) x (2 x 2) x (3 x 3) x 2
The factor, 2, at the end, does not have a pair. Therefore, we must divide 1152 by 2 to make a perfect square. The new number is:
(2 x 2) x (2 x 2) x (2 x 2) x (3 x 3) = 576
Taking one factor from each pair on the LHS, the square root of the new number is 2 x 2 x 2 x 3, which is equal to 24.
Question 7: The product of two numbers is 1296. If one number is 16 times the other, find the numbers.
Answer 7: Let the two numbers be a and b.
From the first statement, we have:
a x b = 1296
If one number is 16 times the other, then we have:
b = 16 x a.
Substituting this value in the first equation, we get:
a x (16 x a) = 1296
By simplifying both sides, we get:
a2 = 1296/16 = 81
Hence, a is the square root of 81, which is 9.
To find b, use equation b = 16 x a.
Since a = 9:
b = 16 x 9 = 144
So, the two numbers satisfying the question are 9 and 144.
Question 8: A welfare association collected Rs 202500 as donation from the residents. If each paid as many rupees as there were residents, find the number of residents.
Answer 8: Let R be the number of residents.
Let r be the money in rupees donated by each resident.
Total donation = R x r = 202500
Since the money received as donation is the same as the number of residents:
∴ r = R.
Substituting this in the first equation, we get:
R x R = 202500
R2 = 202500
R2 = (2 x 2) x (5 x 5) x (5 x 5) x (3 x 3)2
R = 2 x 5 x 5 x 3 x 3 = 450
So, the number of residents is 450.
Question 9: A society collected Rs 92.16. Each member collected as many paise as there were members. How many members were there and how much did each contribute?
Answer 9: Let M be the number of members.
Let r be the amount in paise donated by each member.
The total contribution can be expressed as follows:
M x r = Rs 92.16 = 9216 paise
Since the amount received as donation is the same as the number of members:
∴ r = M
Substituting this in the first equation, we get:
M x M = 9216
M2 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3
M2 = (2 x 2) x (2 x 2) x (2 x 2) x (2 x 2) x (2 x 2) x (3 x 3)
M = 2 x 2 x 2 x 2 x 2 x 3 = 96
To find r, we can use the relation r = M.
Let M be the number of members.
Let r be the amount in paise donated by each member.
The total contribution can be expressed as follows:
M x r = Rs 92.16 = 9216 paise
Since the amount received as donation is the same as the number of members:
∴ r = 96
So, there are 96 members and each paid 96 paise.
Question 10: A school collected Rs 2304 as fees from its students. If each student paid as many paise as there were students in the school, how many students were there in the school?
Answer 10: Let S be the number of students.
Let r be the money donated by each student.
The total contribution can be expressed by (S)(r) = Rs 2304
Since each student paid as many paise as the number of students, then r = S. Substituting this in the first equation, we get:
S x S = 2304
S2 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3
S2 = (2 x 2) x (2 x 2) x (2 x 2) x (2 x 2) x (3 x 3)
S = 2 x 2 x 2 x 2 x 3 = 48
So, there are 48 students in total in the school.
Question 11: The area of a square field is 5184 cm2. A rectangular field, whose length is twice its breadth has its perimeter equal to the perimeter of the square field. Find the area of the rectangular field.
Answer 11: First, we have to find the perimeter of the square.
The area of the square is r2, where r is the side of the square.
Then, we have the equation as follows:
r2 = 5184 = (2 x 2) x (2 x 2) x (2 x 2) x (3 x 3) x (3 x 3)
Taking the square root, we get r = 2 x 2 x 2 x 3 x 3 = 72
Hence the perimeter of the square is 4 x r = 288 m
Now let L be the length of the rectangular field.
Let W be the width of the rectangular field.
The perimeter is equal to the perimeter of square.
Hence, we have:
2(L + W) = 288
Moreover, since the length is twice the width:
L = 2 x W.
Substituting this in the previous equation, we get:
2 x (2 x W + W) = 288
3 x W = 144
W = 48
To find L:
L = 2 x W = 2 x 48 = 96
∴ Area of the rectangular field = L x W = 96 x 48 = 4608 m2
Question 12: Find the least square number, exactly divisible by each one of the numbers:
(i) 6, 9, 15 and 20
(ii) 8, 12, 15 and 20
Answer 12: (i) The smallest number divisible by 6, 9, 15 and 20 is their L.C.M., which is equal to 60.
Factorising 60 into its prime factors:
60 = 2 x 2 x 3 x 5
Grouping them into pairs of equal factors:
60 = (2 x 2) x 3 x 5
The factors 3 and 5 are not paired. To make 60 a perfect square, we have to multiply it by 3 x 5, i.e . by 15.
The perfect square is 60 x 15, which is equal to 900.
(i) The smallest number divisible by 8, 12, 15 and 20 is their L.C.M., which is equal to 120.
Factorising 120 into its prime factors:
120 = 2 x 2 x 2 x 3 x 5
Grouping them into pairs of equal factors:
120 = (2 x 2) x 2 x 3 x 5
The factors 2, 3 and 5 are not paired. To make 120 into a perfect square, we have to multiply it by 2 x 3 x 5, i.e. by 30.
The perfect square is 120 x 30, which is equal to 3600.
Question 13: Find the square roots of 121 and 169 by the method of repeated subtraction.
Answer 13: To find the square root of 121:
121 − 1 = 120
120 − 3 = 117
117 − 5 = 112
112 − 7 = 105
105 − 9 = 96
96 − 11 = 85
85 − 13 = 72
72 − 15 = 57
57 − 17 = 40
40 − 19 = 21
21 − 21 = 0
In total, there are 11 numbers to subtract from 121. Hence, the square root of 121 is 11.
To find the square root of 169:
169 − 1 = 168
168 − 3 = 165
165 − 5 = 160
160 − 7 = 153
153 − 9 = 144
144 − 11 = 133
133 − 13 = 120
120 − 15 = 105
105 − 17 = 88
88 − 19 = 69
69 − 21 = 48
48 − 23 = 25
25 − 25 = 0
In total, there are 13 numbers to subtract from 169. Hence, the square root of 169 is 13.
Question 14 Write the prime factorization of the following numbers and hence find their square roots.
(i) 7744
(ii) 9604
(iii) 5929
(iv) 7056
Answer 14: (i) The prime factorisation of 7744:
7744 = 2 × 2 × 2 × 2 × 2 × 2 × 11 × 11
Grouping them into pairs of equal factors, we get:
7744 = (2 × 2) × (2 × 2) × (2 × 2) × (11 × 11)
Taking one factor from each pair, we get :
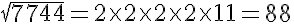
(ii) The prime factorisation of 9604:
9604 = 2 × 2 × 7 × 7 × 7 × 7
Grouping them into pairs of equal factors, we get:
9604 = (2 × 2) × (7 × 7) × (7 × 7)
Taking one factor from each pair, we get:
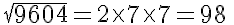
(iii) The prime factorisation of 5929:
5929 = 7 x 7 x 11 x 11
Grouping them into pairs of equal factors, we get:
5929 = (7 × 7) × (11 × 11)
Taking one factor from each pair, we get:
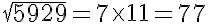
(iv) The prime factorisation of 7056:
7056 = 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
Grouping them into pairs of equal factors, we get:
7056 = (2 × 2) × (2 × 2) × (3 × 3) × (7 × 7)
Taking one factor from each pair, we get:
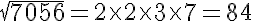
Question 15: The students of class VIII of a school donated Rs 2401 for PM's National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Answer 15: Let S be the number of students.
Let r be the amount in rupees donated by each student.
The total donation can be expressed by:
S × r = Rs. 2401
Since the total amount in rupees is equal to the number of students, r is equal to S.
Substituting this in the first equation:
S × S = 2401
S2 = (7 × 7) × (7 × 7)
S = 7 × 7 = 49
So, there are 49 students in the class.
Question 16: A PT teacher wants to arrange maximum possible number of 6000 students in a field such that the number of rows is equal to the number of columns. Find the number of rows if 71 were left out after arrangement.
Answer 16: Since 71 students were left out, there are only 5929 (6000 − 71) students remaining.
Hence, the number of rows or columns is simply the square root of 5929.
Factorising 5929 into its prime factors:
5929 = 7 × 7 × 11 × 11
Grouping them into pairs of equal factors:
5929 = (7 x 7) x (11 x 11)
The square root of 5929
=
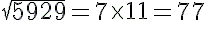
Hence, in the arrangement, there were 77 rows of students.
The document RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) | RD Sharma Solutions for Class 8 Mathematics is a part of the Class 8 Course RD Sharma Solutions for Class 8 Mathematics.
All you need of Class 8 at this link: Class 8
FAQs on RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) - RD Sharma Solutions for Class 8 Mathematics
| 1. What is the difference between a square and a square root? |  |
Ans. A square of a number is the product of that number multiplied by itself. For example, the square of 4 is 4 x 4 = 16. On the other hand, a square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because 4 x 4 = 16.
| 2. How can I find the square root of a number without using a calculator? | |
Ans. To find the square root of a number without using a calculator, you can use the prime factorization method. First, find the prime factors of the number. Then, group the factors in pairs and take one factor from each pair. Multiply these factors together to get the square root of the original number.
| 3. Can a perfect square be a negative number? | |
Ans. No, a perfect square cannot be a negative number. A perfect square is always a non-negative number because it is the square of a real number. However, if we consider complex numbers, then the square of a complex number can be negative.
| 4. How can I determine if a number is a perfect square? | |
Ans. To determine if a number is a perfect square, you can take the square root of the number. If the square root is a whole number, then the original number is a perfect square. For example, the square root of 25 is 5, which is a whole number, so 25 is a perfect square.
| 5. What is the square root of 0? | |
Ans. The square root of 0 is 0. When a number is multiplied by itself to get 0, the number itself is 0. Therefore, the square root of 0 is 0.
Related Exams
About this Document
|
4.98/5 Rating |
|
Nov 23, 2024 Last updated |
Document Description: RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) for Class 8 2024 is part of RD Sharma Solutions for Class 8 Mathematics preparation.
The notes and questions for RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) have been prepared according to the Class 8 exam syllabus. Information about RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) covers topics
like and RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) Example, for Class 8 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3).
Introduction of RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) in English is available as part of our RD Sharma Solutions for Class 8 Mathematics
for Class 8 & RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) in Hindi for RD Sharma Solutions for Class 8 Mathematics course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) | RD Sharma Solutions for Class 8 Mathematics
Description
Full syllabus notes, lecture & questions for RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) | RD Sharma Solutions for Class 8 Mathematics - Class 8 | Plus excerises question with solution to help you revise complete syllabus for RD Sharma Solutions for Class 8 Mathematics | Best notes, free PDF download
Information about RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3)
In this doc you can find the meaning of RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) defined & explained in the simplest way possible. Besides explaining types of
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) tests, examples and also practice Class 8
tests
|
Explore Courses for Class 8 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) | RD Sharma Solutions for Class 8 Mathematics
,Semester Notes
,ppt
,mock tests for examination
,Free
,Extra Questions
,Important questions
,RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) | RD Sharma Solutions for Class 8 Mathematics
,Previous Year Questions with Solutions
,study material
,MCQs
,video lectures
,past year papers
,Viva Questions
,shortcuts and tricks
,practice quizzes
,Exam
,RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) | RD Sharma Solutions for Class 8 Mathematics
,Objective type Questions
,Summary
,Sample Paper
;
Additional Information about RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) for Class 8 Preparation
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) Free PDF Download
The RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) now and kickstart your journey towards success in the Class 8 exam.
Importance of RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3)
The importance of RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) Notes
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3).
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) Notes on EduRev are your ultimate resource for success.
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) Class 8 Questions
The "RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) on the App
Students of Class 8 can study RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3),
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-3) is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup