Class 8 Exam > Class 8 Notes > RD Sharma Solutions for Class 8 Mathematics > RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-4)
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-4) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Find the square root of each of the following by long division method:
(i) 12544
(ii) 97344
(iii) 286225
(iv) 390625
(v) 363609
(vi) 974169
(vii) 120409
(viii) 1471369
(ix) 291600
(x) 9653449
(xi) 1745041
(xii) 4008004
(xiii) 20657025
(xiv) 152547201
(xv) 20421361
(xvi) 62504836
(xvii) 82264900
(xviii) 3226694416
(xix) 6407522209
(xx) 3915380329
Answer 1: (i)
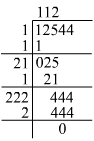
Hence, the square root of 12544 is 112.
(ii)

Hence, the square root of 97344 is 312.
(iii)
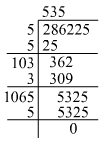
Hence, the square root of 286225 is 535.
(iv)

Hence, the square root of 390625 is 625.
(v)
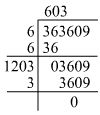
Hence, the square root of 363609 is 603.
(vi)
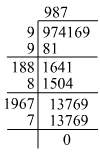
Hence, the square root of 974169 is 987.
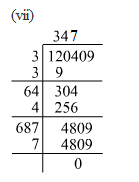
Hence, the square root of 120409 is 347.
(viii)
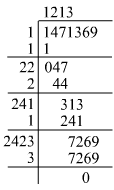
Hence, the square root of 1471369 is 1213.
(ix)
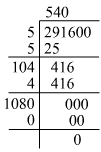
Hence, the square root of 291600 is 540.
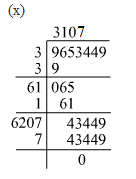
Hence, the square root of 9653449 is 3107.
(xi)
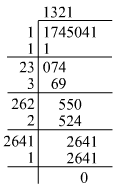
Hence, the square root of 1745041 is 1321.
(xii)
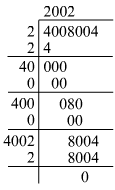
Hence, the square root of 4008004 is 2002.
(xiii)

Hence, the square root of 20657025 is 4545.
(xiv)

Hence, the square root of 152547201 is 12351.
(xv)
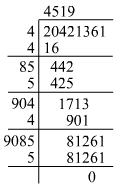
Hence, the square root of 20421361 is 4519.
(xvi)

Hence, the square root of 6250486 is 7906.
(xvii)

Hence, the square root of 82264900 is 9070.
(xviii)

Hence, the square root of 3226694416 is 56804.
(xix)

Hence, the square root of 6407522209 is 80047.
(xx)

Hence, the square root of 3915380329 is 625763.
Question 2: Find the least number which must be subtracted from the following numbers to make them a perfect square:
(i) 2361
(ii) 194491
(iii) 26535
(iv) 16160
(v) 4401624
Answer 2: (i) Using the long division method:
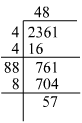
We can see that 2361 is 57 more than 472. Hence, 57 must be subtracted from 2361 to get a perfect square.
(ii) Using the long division method:
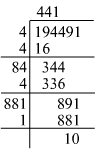
We can see that 194491 is 10 more than 4412. Hence, 10 must be subtracted from 194491 to get a perfect square.
(iii) Using the long division method:
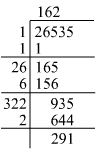
We can see that 26535 is 291 more than 1622. Hence, 291 must be subtracted from 26535 to get a perfect square.
(iv) Using the long division method:
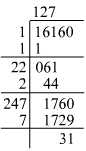
We can see that 16160 is 31 more than 1272. Hence, 31 must be subtracted from 16160 to get a perfect square.
(v) Using the long division method:

We can be see that 4401624 is 20 more than 20982. Hence, 20 must be subtracted from 4401624 to get a perfect square.
Question 3: Find the least number which must be added to the following numbers to make them a perfect square:
(i) 5607
(ii) 4931
(iii) 4515600
(iv) 37460
(v) 506900
Answer 3:(i) Using the long division method:
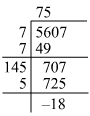
We can see that 5607 is 18 more than 752. Hence, we have to add 18 to 5607 to get a perfect square.
(ii) Using the long division method:

We can see that 4931 is 110 more than 712. Hence, we have to add 110 to 4931 to get a perfect square.
(iii) Using the long division method:

We can see that 4515600 is 25 more than 21252. Hence, we have to add 25 to 4515600 to get a perfect square.
(iv) Using the long division method:
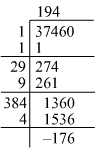
We can see that 37460 is 176 more than 1942. Hence, we have to add 176 to 37460 to get a perfect square.
(v) Using the long division method:
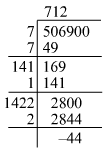 We can see that 506900 is 44 more than 7122. Hence, we have to add 44 to 506900 to get a perfect square.
We can see that 506900 is 44 more than 7122. Hence, we have to add 44 to 506900 to get a perfect square.
Question 4: Find the greatest number of 5 digits which is a perfect square.
Answer 4: The greatest number with five digits is 99999. To find the greatest square number with five digits, we must find the smallest number that must be subtracted from 99999 in order to make a perfect square. For that, we have to find the square root of 99999 by the long division method as follows:

Hence, we must subtract 143 from 99999 to get a perfect square:
99999 − 143 = 99856
Question 5: Find the least number of 4 digits which is a perfect square.
Answer 5: The least number with four digits is 1000. To find the least square number with four digits, we must find the smallest number that must be added to 1000 in order to make a perfect square. For that, we have to find the square root of 1000 by the long division method as shown below:
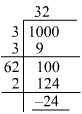
1000 is 24 (124 − 100) less than the nearest square number 322. Thus, 24 must be added to 1000 to be a perfect square.
1000 + 24 = 1024
Hence, the smallest perfect square number with four digits is 1024.
Question 6: Find the least number of six digits which is a perfect square.
Answer 6: The least number with six digits is 100000. To find the least square number with six digits, we must find the smallest number that must be added to 100000 in order to make a perfect square. For that, we have to find the square root of 100000 by the long division method as follows:
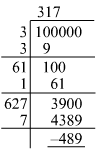
100000 is 489 (4389 − 3900) less than 3172. Hence, to be a perfect square, 489 should be added to 100000.
100000 + 489 = 100489
Hence, the least number of six digits that is a perfect square is 100489.
Question 7: Find the greatest number of 4 digits which is a perfect square.
Answer 7: The greatest number with four digits is 9999. To find the greatest perfect square with four digits, we must find the smallest number that must be subtracted from 9999 in order to make a perfect square. For that, we have to find the square root of 9999 by the long division method as shown below:

We must subtract 198 from 9999 to make a perfect square:
9999 − 198 = 9801
Hence, the greatest perfect square with four digits is 9801.
Question 8: A General arranges his soldiers in rows to form a perfect square. He finds that in doing so, 60 soldiers are left out. If the total number of soldiers be 8160, find the number of soldiers in each row.
Answer 8: 60 soldiers are left out.
∴ Remainaing soldiers = 8160 − 60 = 8100
The number of soldiers in each row to form a perfect square would be the square root of 8100. We have to find the square root of 8100 by the long division method as shown below:
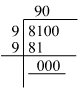
Hence, the number of soldiers in each row to form a perfect square is 90.
Question 9: The area of a square field is 60025 m2. A man cycles along its boundary at 18 km/hr. In how much time will he return at the starting point?
Answer 9: Area of the square field = 60025 m2
The length of the square field would be the square root of 60025.
Using the long division method:
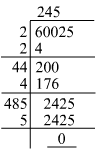
Hence, the length of the square field is 245 m.
The square has four sides, so the number of boundaries of the field is 4.
The distance s covered by the man = 245 m × 4 = 980 m = 0.98 km
If the velocity v is 18 km/hr, the required time t can be calculated using the following formula:
t= s/v
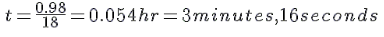
So, the man will return to the starting point after 3 minutes and 16 seconds.
Question 10: The cost of levelling and turfing a square lawn at Rs 2.50 per m2 is Rs 13322.50. Find the cost of fencing it at Rs 5 per metre.
Answer 10: First, we have to find the area of the square lawn, which the total cost divided by the cost of levelling and turfing per square metre:
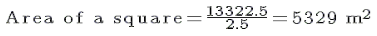
The length of one side of the square is equal to the square root of the area. We will use the long division method to find it as shown below:
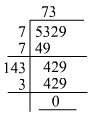 ∴ Length of one side of the square = 73 m
∴ Length of one side of the square = 73 m
The circumference of the square is 73 × 4 = 292 m
∴ Total cost of fencing the lawn at Rs. 5 per metre = 292 × 5 = Rs. 1460
Question 11: Find the greatest number of three digits which is a perfect square.
Answer 11: The greatest number with three digits is 999. To find the greatest perfect square with three digits, we must find the smallest number that must be subtracted from 999 in order to get a perfect square. For that, we have to find the square root by the long division method as shown below:
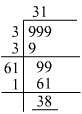
So, 38 must be subtracted from 999 to get a perfect square.
999 − 38 = 961
961 = 312
Hence, the greatest perfect square with three digits is 961.
Question 12: Find the smallest number which must be added to 2300 so that it becomes a perfect square.
Answer 12: To find the square root of 2300, we use the long division method:

23000 is 4 (704 − 700) less than 482. Hence, 4 must be added to 2300 to get a perfect square.
The document RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-4) | RD Sharma Solutions for Class 8 Mathematics is a part of the Class 8 Course RD Sharma Solutions for Class 8 Mathematics.
All you need of Class 8 at this link: Class 8
FAQs on RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-4) - RD Sharma Solutions for Class 8 Mathematics
| 1. What are squares and square roots? |  |
Ans. Squares are the product of a number multiplied by itself, while square roots are the inverse operation of finding the number whose square gives a specific value. For example, the square of 4 is 16, and the square root of 16 is 4.
| 2. How can I find the square root of a number without a calculator? |  |
Ans. To find the square root of a number without a calculator, you can use the prime factorization method. Write the given number as a product of prime factors, then group the factors in pairs. Take one factor from each pair and multiply them to get the square root. Repeat this process until all the factors have been paired and multiplied.
| 3. What is the square root of a perfect square? |  |
Ans. The square root of a perfect square is a whole number. For example, the square root of 16 is 4, and the square root of 81 is 9. Perfect squares are numbers that can be expressed as the square of an integer.
| 4. Can square roots be negative? |  |
Ans. Square roots are typically positive, but they can also be negative. When we take the square root of a positive number, we get both a positive and a negative square root. For example, the square root of 25 is ±5, as both 5 and -5, when squared, give 25.
| 5. How can I simplify a square root expression? |  |
Ans. To simplify a square root expression, you can factor out any perfect square factors from inside the square root sign. Then, take the square root of the perfect square factors and leave the remaining factors inside the square root sign. This process helps in simplifying the square root expression and making it easier to work with.
Related Searches





















