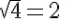RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-5) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Find the square root of:
(i) 441/961
(ii) 324/841
(iii) 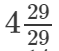
(iv) 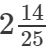
(v) 
(vi) 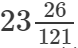
(vii) 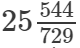
(viii) 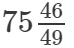
(ix) 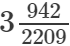
(x) 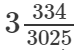
(xi) 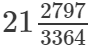
(xii) 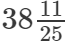
(xiii) 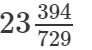
(xiv) 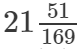
(xv) 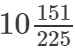
Answer 1: (i) We know:
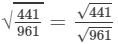
Now, let us compute the square roots of the numerator and the denominator separately.
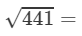
 =3×7=21
=3×7=21

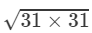 =31
=31
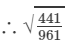
=21/31
(ii)We know:
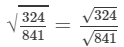
Now, let us compute the square roots of the numerator and the denominator separately.
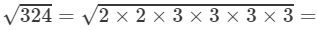 2×3×3=18
2×3×3=18
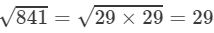
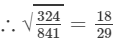
(iii) By looking at the book's answer key, the fraction should be 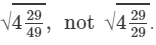 We know:
We know:
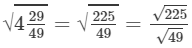
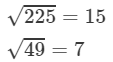
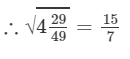
(iv) We know:
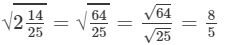
(v) We know:
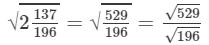
Now, let us compute the square roots of the numerator and the denominator separately.

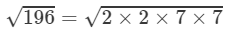 =2×7=14
=2×7=14
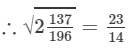
(vi) We know:
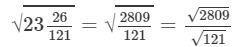
Now, let us compute the square roots of the numerator and the denominator separately.

(vii) We know:
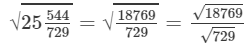
Now, let us compute the square roots of the numerator and the denominator separately.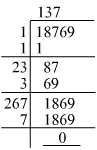
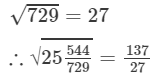
(viii) We know:
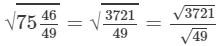
Now, let us compute the square roots of the numerator and the denominator separately.
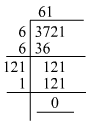
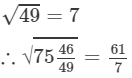
(ix) We know:
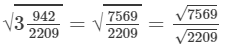
Now, let us compute the square roots of the numerator and the denominator separately.
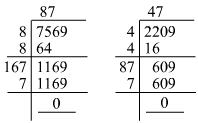
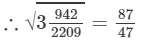
(x) We know:
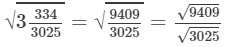
Now, let us compute the square roots of the numerator and the denominator separately.
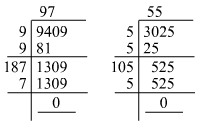
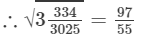
(xi) We know:
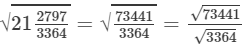
Now, let us compute the square roots of the numerator and the denominator separately.

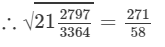
(xii) We know:
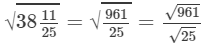
Now, let us compute the square roots of the numerator and the denominator separately.
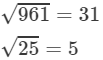
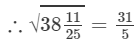
(xiii) We know:
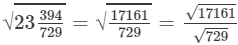
Now, let us compute the square roots of the numerator and the denominator separately.

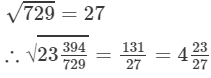
(xiv) We know:
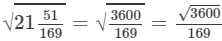
Now, let us compute the square roots of the numerator and the denominator separately.
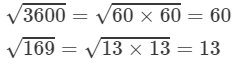
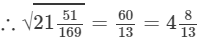
(xv) We know:
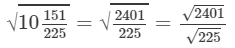
Now let us compute the square roots of the numerator and the denominator separately.
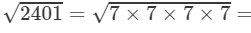 7×7=49
7×7=49
 3×5=15
3×5=15
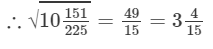
Question 2: Find the value of:
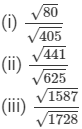
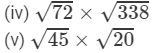
Answer 2: (i) We have:
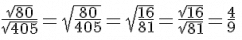
(ii) Computing the square roots:
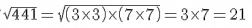
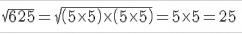
∴ 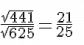
(iii) We have:
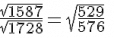 (by dividing both numbers by 3)
(by dividing both numbers by 3)
Computing the square roots of the numerator and the denominator:
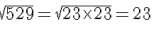
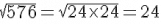
∴∴ 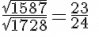
(iv) We have:
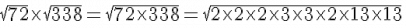
=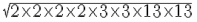
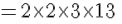
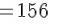
(v) We have:
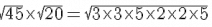

= 30
Question 3: The area of a square field is 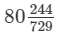 square metres. Find the length of each side of the field.
square metres. Find the length of each side of the field.
Answer 3: The length of one side is the square root of the area of the field. Hence, we need to calculate the value of 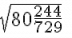
We have
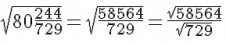
Now, to calculate the square root of the numerator and the denominator:
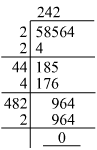
We know that:
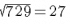
Therefore, length of one side of the field 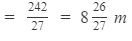
Question 4: The area of a square field is 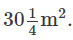 Calculate the length of the side of the square.
Calculate the length of the side of the square.
Answer 4: The length of one side is equal to the square root of the area of the field. Hence, we just need to calculate the value of 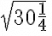 .
.
We have:
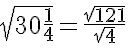
Now, calculating the square root of the numerator and the denominator:
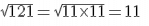
Therefore, the length of the side of the square = 
Question 5: Find the length of a side of a square playground whose area is equal to the area of a rectangular field of diamensions 72 m and 338 m.
Answer 5: The area of the playground = 72 × 338 = 24336 m2
The length of one side of a square is equal to the square root of its area. Hence, we just need to find the square root of 24336.

Hence, the length of one side of the playground is 156 metres.
FAQs on RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-5) - RD Sharma Solutions for Class 8 Mathematics
| 1. What are squares and square roots? |  |
| 2. How do you find the square of a number? |  |
| 3. What is the square root of a perfect square? |  |
| 4. How do you find the square root of a number? |  |
| 5. What are the properties of squares and square roots? |  |