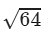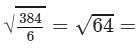Class 8 Exam > Class 8 Notes > RD Sharma Solutions for Class 8 Mathematics > RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2)
RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 15: Find the volume of a cube, one face of which has an area of 64 m2.
Answer 15: Area of a face of cube is given by:
As2, where s = Side of the cube
Further, volume of a cube is given by:
V=s3, where s = Side of the cube
It is given that the area of one face of the cube is 64 m2. Therefore we have:
s2=64⇒s=
=8 m
Now, volume is given by:
V=s3=83⇒V= 8×8×8 =512 m3
Thus, the volume of the cube is 512 m3.
Question 16: Find the volume of a cube whose surface area is 384 m2.
Answer 16: Surface area of a cube is given by:
SA=6s2, where s = Side of the cube
Further, volume of a cube is given by:
V=s3, where s = Side of the cube
It is given that the surface area of the cube is 384 m2. Therefore, we have:
6s2=384⇒s= 8 m
Now, volume is given by:
V=s3=83⇒V= 8×8×8 =512 m3
Thus, the required volume is 512 m3.
Question 17: Evaluate the following:
(i) {(52+122)1/2}3
(ii) {(62+82)1/2}3
Answer 17: (i)
To evaluate the value of the given expression, we can proceed as follows:
(52+122)1/2}3
={(25+144)1/2}3
={(169)1/2}3
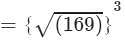
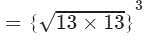
={13}3=13×13×13=2197
(ii) To evaluate the value of the given expression, we can proceed as follows:
{(62+82)1/2}3={(36+64)1/2}3={(100)1/2}3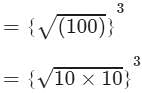 
={10}3=10×10×10=1000
Question 18: Write the units digit of the cube of each of the following numbers:
31, 109, 388, 833, 4276, 5922, 77774, 44447, 125125125
Answer 18: Properties:
If a numbers ends with digits 1, 4, 5, 6 or 9, its cube will have the same ending digit.
If a number ends with 2, its cube will end with 8.
If a number ends with 8, its cube will end with 2.
If a number ends with 3, its cube will end with 7.
If a number ends with 7, its cube will end with 3.
From the above properties, we get:
Cube of the number 31 will end with 1.
Cube of the number 109 will end with 9.
Cube of the number 388 will end with 2.
Cube of the number 833 will end with 7.
Cube of the number 4276 will end with 6.
Cube of the number 5922 will end with 8.
Cube of the number 77774 will end with 4.
Cube of the number 44447 will end with 3.
Cube of the number 125125125 will end with 5.
Question 19: Find the cubes of the following numbers by column method:
(i) 35
(ii) 56
(iii) 72
Answer 19: (i) We have to find the cube of 35 using column method. We have: a=3 and b=5
| Column I a3 | Column II 3×a2×b | Column III 3×a×b2 | Column IV b3 |
| 33=27 | 3×a2×b=3×32×5=135 | 3×a×b2=3×3×52=225 | 53=125 |
| +15 | +23 | + 12 | 125 |
| 42 | 158 | 237 | |
| 42 | 8 | 7 | 5 |
Thus, cube of 35 is 42875.
(ii) We have to find the cube of 56 using column method. We have: a=5 and b=6
| Column I a3 | Column II 3×a2×b | Column III 3×a×b2 | Column IV b3 |
| 53=125 | 3×a2×b=3×52×6=450 | 3×a×b2=3×5×62=540 | 63=216 |
| +50 | +56 | + 21 | 216 |
| 175 | 506 | 561 | |
| 175 | 6 | 1 | 6 |
Thus, cube of 56 is 175616.
(iii) We have to find the cube of 72 using column method. We have: a=7 and b=2
| Column I a3 | Column II 3×a2×b | Column III 3×a×b2 | Column IV b3 |
| 73=343 | 3×a2×b=3×72×2=294 | 3×a×b2=3×7×22=84 | 23=8 |
| +30 | +8 | +0 | 8 |
| 373 | 302 | 84 | |
| 373 | 2 | 4 | 8 |
Thus, cube of 72 is 373248.
Question 20: Which of the following numbers are not perfect cubes?
(i) 64
(ii) 216
(iii) 243
(iv) 1728
Answer 20: (i) On factorising 64 into prime factors, we get:
64=2×2×2×2×2×2
On grouping the factors in triples of equal factors, we get:
64={2×2×2}×{2×2×2}
It is evident that the prime factors of 64 can be grouped into triples of equal factors and no factor is left over. Therefore, 64 is a perfect cube.
(ii) On factorising 216 into prime factors, we get:
216=2×2×2×3×3×3
On grouping the factors in triples of equal factors, we get:
216={2×2×2}×{3×3×3}
It is evident that the prime factors of 216 can be grouped into triples of equal factors and no factor is left over. Therefore, 216 is a perfect cube.
(iii) On factorising 243 into prime factors, we get:
243=3×3×3×3×3
On grouping the factors in triples of equal factors, we get:
243={3×3×3}×3×3
It is evident that the prime factors of 243 cannot be grouped into triples of equal factors such that no factor is left over. Therefore, 243 is a not perfect cube.
(iv) On factorising 1728 into prime factors, we get:
1728=2×2×2×2×2×2×3×3×3
On grouping the factors in triples of equal factors, we get:
1728={2×2×2}×{2×2×2}×{3×3×3}
It is evident that the prime factors of 1728 can be grouped into triples of equal factors and no factor is left over. Therefore, 1728 is a perfect cube.
Thus, (iii) 243 is the required number, which is not a perfect cube.
Question 21: For each of the non-perfect cubes in Q. No. 20 find the smallest number by which it must be
(a) multiplied so that the product is a perfect cube.
(b) divided so that the quotient is a perfect cube.
Answer 21: The only non-perfect cube in question number 20 is 243.
(a) On factorising 243 into prime factors, we get:
243=3×3×3×3×3
On grouping the factors in triples of equal factors, we get:
243={3×3×3}×3×3
It is evident that the prime factors of 243 cannot be grouped into triples of equal factors such that no factor is left over. Therefore, 243 is not a perfect cube. However, if the number is multiplied by 3, the factors can be grouped into triples of equal factors such that no factor is left over.
Thus, 243 should be multiplied by 3 to make it a perfect cube.
(b) On factorising 243 into prime factors, we get:
243=3×3×3×3×3
On grouping the factors in triples of equal factors, we get:
243={3×3×3}×3×3
It is evident that the prime factors of 243 cannot be grouped into triples of equal factors such that no factor is left over. Therefore, 243 is not a perfect cube. However, if the number is divided by (3×3=9), the factors can be grouped into triples of equal factors such that no factor is left over.
Thus, 243 should be divided by 9 to make it a perfect cube.
Question 22: By taking three different values of n verify the truth of the following statements:
(i) If n is even , then n3 is also even.
(ii) If n is odd, then n3 is also odd.
(iii) If n leaves remainder 1 when divided by 3, then n3 also leaves 1 as remainder when divided by 3.
(iv) If a natural number n is of the form 3p + 2 then n3 also a number of the same type.
Answer 22: (i) Let the three even natural numbers be 2, 4 and 8.
Cubes of these numbers are:
23=8, 43=64, 83=512
By divisibility test, it is evident that 8, 64 and 512 are divisible by 2.
Thus, they are even.
This verifies the statement.
(ii) Let the three odd natural numbers be 3, 9 and 27.
Cubes of these numbers are:
33=27, 93=729, 273=19683
By divisibility test, it is evident that 27, 729 and 19683 are divisible by 3.
Thus, they are odd.
This verifies the statement.
(iii) Three natural numbers of the form (3n + 1) can be written by choosing n=1,2,3... etc.
Let three such numbers be 4,7 and 10.
Cubes of the three chosen numbers are:
43=64, 73=343 and 103=1000
Cubes of 4,7 and 10 can expressed as:
64=3×21+1, which is of the form (3n + 1) for n = 21
343=3×114+1, which is of the form (3n + 1) for n = 114
1000=3×333+1, which is of the form (3n + 1) for n = 333
Cubes of 4,7, and 10 can be expressed as the natural numbers of the form (3n + 1) for some natural number n. Hence, the statement is verified.
(iv) Three natural numbers of the form (3p + 2) can be written by choosing p=1,2,3... etc.
Let three such numbers be 5,8 and 11.
Cubes of the three chosen numbers are:
53=125, 83=512 and 113=1331
Cubes of 5,8, and 11 can be expressed as:
125=3×41+2, which is of the form (3p + 2) for p = 41
512=3×170+2, which is of the form (3p + 2) for p = 170
1331=3×443+2, which is of the form (3p + 2) for p = 443
Cubes of 5,8, and 11 could be expressed as the natural numbers of the form (3p + 2) for some natural number p. Hence, the statement is verified.
Question 23: Write true (T) or false (F) for the following statements:
(i) 392 is a perfect cube.
(ii) 8640 is not a perfect cube.
(iii) No cube can end with exactly two zeros.
(iv) There is no perfect cube which ends in 4.
(v) For an integer a, a3 is always greater than a2.
(vi) If a and b are integers such that a2 > b2, then a3 > b3.
(vii) If a divides b, then a3 divides b3.
(viii) If a2 ends in 9, then a3 ends in 7.
(ix) If a2 ends in 5, then a3 ends in 25.
(x) If a2 ends in an even number of zeros, then a3 ends in an odd number of zeros.
Answer 23: (i) False
On factorising 392 into prime factors, we get:
392=2×2×2×7×7
On grouping the factors in triples of equal factors, we get:
392={2×2×2}×7×7
It is evident that the prime factors of 392 cannot be grouped into triples of equal factors such that no factor is left over. Therefore, 392 is not a perfect cube.
(ii) True
On factorising 8640 into prime factors, we get:
8640=2×2×2×2×2×2×3×3×3×5
On grouping the factors in triples of equal factors, we get:
8640={2×2×2}×{2×2×2}×{3×3×3}×5
It is evident that the prime factors of 8640 cannot be grouped into triples of equal factors such that no factor is left over. Therefore, 8640 is not a perfect cube.
(iii) True
Because a perfect cube always ends with multiples of 3 zeros, e.g., 3 zeros, 6 zeros etc.
(iv) False.
64 is a perfect cube, and it ends with 4.
(v) False
It is not true for a negative integer. Example: (−5)2=25; (−5)3=−125⇒(−5)3<(−5)2
(vi) False
It is not true for negative integers. Example: (−5)2>(−4)2 but (−5)3<(−4)3
(vii) True
∵ a divides b
∵ a divides b
∴ b = ak for some k
=k3⇒b3=a3(k3)
∴ a3 divides b3
(viii) False
a3 ends in 7 if a ends with 3.
But for every a2 ending in 9, it is not necessary that a is 3.
E.g., 49 is a square of 7 and cube of 7 is 343.
(ix) False
∵ 352=1225 but 353=42875
(x) False
∵ 1002=10000 and 1003 = 100000
Question 24: Find the cubes of:
(i) −11
(ii) −12
(iii) −21
Answer 24: (i) Cube of −11 is given as:
(−11)3=−11×−11×−11=−1331
Thus, the cube of 11 is (−1331).
(ii) Cube of −12 is given as:
(−12)3=−12×−12×−12=−1728
Thus, the cube of −12 is (−1728).
(iii) Cube of −21 is given as:
(−21)3=−21×−21×−21=−9261
Thus, the cube of −21 is (−9261).
Question 25: Which of the following numbers are cubes of negative integers
(i) −64
(ii) −1056
(iii) −2197
(iv) −2744
(v) −42875
Answer 25: In order to check if a negative number is a perfect cube, first check if the corresponding positive integer is a perfect cube. Also, for any positive integer m, −m3 is the cube of −m.
(i) On factorising 64 into prime factors, we get:
64=2×2×2×2×2×2
On grouping the factors in triples of equal factors, we get:
64={2×2×2}×{2×2×2}
It is evident that the prime factors of 64 can be grouped into triples of equal factors and no factor is left over. Therefore, 64 is a perfect cube. This implies that −64 is also a perfect cube.
Now, collect one factor from each triplet and multiply, we get:
2×2=4
This implies that 64 is a cube of 4.
Thus, −64 is the cube of −4.
(ii) On factorising 1056 into prime factors, we get:
1056=2×2×2×2×2×3×11
On grouping the factors in triples of equal factors, we get:
1056={2×2×2}×2×2×3×11
It is evident that the prime factors of 1056 cannot be grouped into triples of equal factors such that no factor is left over. Therefore, 1056 is not a perfect cube. This implies that −1056 is not a perfect cube as well.
(iii) On factorising 2197 into prime factors, we get:
2197=13×13×13
On grouping the factors in triples of equal factors, we get:
2197={13×13×13}
It is evident that the prime factors of 2197 can be grouped into triples of equal factors and no factor is left over. Therefore, 2197 is a perfect cube. This implies that −2197 is also a perfect cube.
Now, collect one factor from each triplet and multiply, we get 13.
This implies that 2197 is a cube of 13.
Thus, −2197 is the cube of −13.
(iv) On factorising 2744 into prime factors, we get:
2744=2×2×2×7×7×7
On grouping the factors in triples of equal factors, we get:
2744={2×2×2}×{7×7×7}
It is evident that the prime factors of 2744 can be grouped into triples of equal factors and no factor is left over. Therefore, 2744 is a perfect cube. This implies that −2744 is also a perfect cube.
Now, collect one factor from each triplet and multiply, we get:
2×7=14
This implies that 2744 is a cube of 14.
Thus, −2744 is the cube of −14.
(v) On factorising 42875 into prime factors, we get:
42875=5×5×5×7×7×7
On grouping the factors in triples of equal factors, we get:
42875={5×5×5}×{7×7×7}
It is evident that the prime factors of 42875 can be grouped into triples of equal factors and no factor is left over. Therefore, 42875 is a perfect cube. This implies that −42875 is also a perfect cube.
Now, collect one factor from each triplet and multiply, we get:
5×7=35
This implies that 42875 is a cube of 35.
Thus, −42875 is the cube of −35.
Question 26: Show that the following integers are cubes of negative integers. Also, find the integer whose cube is the given integer.
(i) −5832
(ii) −2744000
Answer 26: In order to check if a negative number is a perfect cube, first check if the corresponding positive integer is a perfect cube. Also, for any positive integer m, −m3 is the cube of −m.
(i) On factorising 5832 into prime factors, we get:
5832=2×2×2×3×3×3×3×3×3
On grouping the factors in triples of equal factors, we get:
5832={2×2×2}×{3×3×3}×{3×3×3}
It is evident that the prime factors of 5832 can be grouped into triples of equal factors and no factor is left over. Therefore, 5832 is a perfect cube. This implies that −5832 is also a perfect cube.
Now, collect one factor from each triplet and multiply, we get:
2×3×3=18
This implies that 5832 is a cube of 18.
Thus, −5832 is the cube of −18.
(ii) On factorising 2744000 into prime factors, we get:
2744000=2×2×2×2×2×2×5×5×5×7×7×7
On grouping the factors in triples of equal factors, we get:
2744000={2×2×2}×{2×2×2}×{5×5×5}×{7×7×7}
It is evident that the prime factors of 2744000 can be grouped into triples of equal factors and no factor is left over. Therefore, 2744000 is a perfect cube. This implies that −2744000 is also a perfect cube.
Now, collect one factor from each triplet and multiply, we get:
2×2×5×7=140
This implies that 2744000 is a cube of 140.
Thus, −2744000 is the cube of −140.
Question 27: Find the cube of:
(vii) 0.3
(viii) 1.5
(ix) 0.08
(x) 2.1
Answer 27:
(i) 
(ii) 
(iii) 
(iv) 
(v) We have:
(vi) We have:
(vii) We have:
=0.027
(viii) We have:
=3.375
(ix) We have:
(x) We have:
=9.261
Question 28: Find which of the following numbers are cubes of rational numbers:
(i) 27/64
(ii) 125/128
(iii) 0.001331
(iv) 0.04
Answer 28: (i) We have:
Therefore, 27/64 is a cube of 3/8.
(ii) We have:
It is evident that 128 cannot be grouped into triples of equal factors; therefore, 125/128 is not a cube of a rational number.
(iii) We have:
0.001331= 
Therefore, 0.001331 is a cube of 11/100.
(iv) We have:
It is evident that 4 and 100 could not be grouped in to triples of equal factors; therefore, 0.04 is not a cube of a rational number.
The document RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) | RD Sharma Solutions for Class 8 Mathematics is a part of the Class 8 Course RD Sharma Solutions for Class 8 Mathematics.
All you need of Class 8 at this link: Class 8
FAQs on RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) - RD Sharma Solutions for Class 8 Mathematics
| 1. What are cubes and cube roots? |  |
Ans. Cubes are numbers that are multiplied by themselves three times. For example, 2 cubed (written as 2^3) is equal to 2 x 2 x 2 = 8. Cube roots, on the other hand, are the opposite operation of cubes. They help us find the number that, when multiplied by itself three times, gives us a given number. For example, the cube root of 8 is 2, since 2 x 2 x 2 = 8.
| 2. How do I find the cube of a number? | |
Ans. To find the cube of a number, you simply multiply the number by itself two more times. For example, to find the cube of 3, you would calculate 3 x 3 x 3 = 27. Similarly, for any other number, you would multiply it by itself twice to find its cube.
| 3. How do I find the cube root of a number? | |
Ans. To find the cube root of a number, you need to find the number that, when multiplied by itself three times, gives you the given number. This can be done using the prime factorization method. You factorize the given number into prime factors and then group them in sets of three. The cube root will be the product of the numbers in each set. For example, to find the cube root of 27, you factorize it as 3 x 3 x 3. Since there is only one set of three numbers, the cube root of 27 is 3.
| 4. How can I simplify expressions involving cubes and cube roots? | |
Ans. To simplify expressions involving cubes and cube roots, you can use the properties of exponents. For example, if you have (a^3)^2, you can simplify it as a^(3 x 2) = a^6. Similarly, if you have the cube root of a number raised to a power, you can simplify it by multiplying the power with 1/3. For example, the cube root of (a^6) can be simplified as (a^6)^(1/3) = a^(6 x 1/3) = a^2.
| 5. How are cubes and cube roots used in real-life applications? | |
Ans. Cubes and cube roots are used in various real-life applications, especially in fields like architecture, engineering, and computer graphics. For example, architects often need to calculate the volume of a cuboid or cube-shaped building, which involves finding the cube of a number. Similarly, engineers use cube roots to calculate the side length of a cube given its volume. In computer graphics, cube roots are used for scaling objects in three dimensions to maintain their proportions.
Related Exams
About this Document
|
4.85/5 Rating |
|
Nov 30, 2024 Last updated |
Document Description: RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) for Class 8 2024 is part of RD Sharma Solutions for Class 8 Mathematics preparation.
The notes and questions for RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) have been prepared according to the Class 8 exam syllabus. Information about RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) covers topics
like and RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) Example, for Class 8 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2).
Introduction of RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) in English is available as part of our RD Sharma Solutions for Class 8 Mathematics
for Class 8 & RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) in Hindi for RD Sharma Solutions for Class 8 Mathematics course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) | RD Sharma Solutions for Class 8 Mathematics
Description
Full syllabus notes, lecture & questions for RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) | RD Sharma Solutions for Class 8 Mathematics - Class 8 | Plus excerises question with solution to help you revise complete syllabus for RD Sharma Solutions for Class 8 Mathematics | Best notes, free PDF download
Information about RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2)
In this doc you can find the meaning of RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) defined & explained in the simplest way possible. Besides explaining types of
RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) tests, examples and also practice Class 8
tests
|
Explore Courses for Class 8 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
past year papers
,mock tests for examination
,Objective type Questions
,Semester Notes
,Important questions
,video lectures
,ppt
,Sample Paper
,shortcuts and tricks
,RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) | RD Sharma Solutions for Class 8 Mathematics
,practice quizzes
,RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) | RD Sharma Solutions for Class 8 Mathematics
,study material
,Previous Year Questions with Solutions
,RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) | RD Sharma Solutions for Class 8 Mathematics
,MCQs
,Free
,Summary
,Viva Questions
,Exam
,Extra Questions
;
Additional Information about RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) for Class 8 Preparation
RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) Free PDF Download
The RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) now and kickstart your journey towards success in the Class 8 exam.
Importance of RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2)
The importance of RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) Notes
RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2).
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) Notes on EduRev are your ultimate resource for success.
RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) Class 8 Questions
The "RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) on the App
Students of Class 8 can study RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2),
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-2) is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup