RD Sharma Solutions for Class 8 Math Chapter 6 - Algebraic Expressions and Identities (Part-4 ) Notes | Study RD Sharma Solutions for Class 8 Mathematics - Class 8

Question 1: Multiply:
(5x + 3) by (7x + 2)

Answer 1: To multiply, we will use distributive law as follows:
(5x+3)(7x+2)=5x(7x+2)+3(7x+2)=(5x×7x+5x×2)+(3×7x+3×2)=(35x2+10x)+(21x+6)=35x2+10x+21x+6=35x2+31x+6Thus, the answer is 35x2+31x+635x2+31x+6. 

Question 2: Multiply:
(2x + 8) by (x − 3)

Answer 2: To multiply the expressions, we will use the distributive law in the following way:
(2x+8)(x−3)=2x(x−3)+8(x−3)=(2x×x−2x×3)+(8x−8×3)=(2x2−6x)+(8x−24)=2x2−6x+8x−24=2x2+2x−242x+8x-3=2xx-3+8x-3=2x×x-2x×3+8x-8×3=2x2-6x+8x-24=2x2-6x+8x-24=2x2+2x-2Thus, the answer is 2x2+2x−242x2+2x-24. 

Question 3: Multiply:
(7x + y) by (x + 5y)

Answer 3: To multiply, we will use distributive law as follows:
(7x+y)(x+5y)=7x(x+5y)+y(x+5y)=7x2+35xy+xy+5y2=7x2+36xy+5y27x+yx+5y=7xx+5y+yx+5y=7x2+35xy+xy+5y2=7x2+36xy+5y2
Thus, the answer is 7x2+36xy+5y27x2+36xy+5y2. 

Question 4: Multiply:
(a − 1) by (0.1a² + 3)

Answer 4: To multiply, we will use distributive law as follows:
(a−1)(0.1a2+3)=0.1a2(a−1)+3(a−1)=0.1a3−0.1a2+3a−3a-10.1a2+3=0.1a2a-1+3a-1=0.1a3-0.1a2+3a-3
Thus, the answer is 0.1a3−0.1a2+3a−30.1a3-0.1a2+3a-3. 

Question 5: Multiply:
(3x² + y²) by (2x² + 3y²)

Answer 5: To multiply, we will use distributive law as follows:
(3x2+y2)(2x2+3y2)=3x2(2x2+3y2)+y2(2x2+3y2)=6x4+9x2y2+2x2y2+3y4=6x4+11x2y2+3y43x2+y22x2+3y2=3x22x2+3y2+y22x2+3y2=6x4+9x2y2+2x2y2+3y4=6x4+11x2y2+3yThus, the answer is 6x4+11x2y2+3y46x4+11x2y2+3y4. 

Question 6: Multiply:

Answer 6: To multiply, we will use distributive law as follows: 

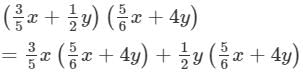
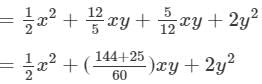
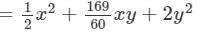
Thus, the answer is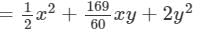 

Question 7: Multiply:
(x⁶ − y⁶) by (x² + y²)

Answer 7: To multiply, we will use distributive law as follows: 

(x6−y6)(x2+y2)=x6(x2+y2)−y6(x2+y2)=(x8+x6y2)−(y6x2+y8)=x8+x6y2−y6x2−y8 Thus, the answer is x8+x6y2−y6x2−y8x8+x6y2-y6x2-y8. 

Question 8: Multiply:
(x² + y²) by (3a + 2b)

Answer 8: To multiply, we will use distributive law as follows: 

(x2+y2)(3a+2b)=x2(3a+2b)+y2(3a+2b)=3ax2+2bx2+3ay2+2by2 Thus, the answer is 3ax2+2bx2+3ay2+2by23ax2+2bx2+3ay2+2by2. 

Question 9: Multiply:
[−3d + (−7f)] by (5d + f)

Answer 9: To multiply, we will use distributive law as follows:
[−3d+(−7f)](5d+f)=(−3d)(5d+f)+(−7f)(5d+f)=(−15d2−3df)+(−35df−7f2)=−15d2−3df−35df−7f2=−15d2−38df−7f2Thus, the answer is −15d2−38df−7f2-15d2-38df-7f2. 

Question 10: Multiply:
(0.8a − 0.5b) by (1.5a − 3b)

Answer 10: To multiply, we will use distributive law as follows:
(0.8a−0.5b)(1.5a−3b)=0.8a(1.5a−3b)−0.5b(1.5a−3b)=1.2a2−2.4ab−0.75ab+1.5b2=1.2a2−3.15ab+1.5b2Thus, the answer is 1.2a2−3.15ab+1.5b21.2a2-3.15ab+1.5b2. 

Question 11: Multiply:
(2x²y² − 5xy²) by (x² − y²)

Answer 11: To multiply, we will use distributive law as follows:

(2x2y2−5xy2)(x2−y2)=2x2y2(x2−y2)−5xy2(x2−y2)=2x4y2−2x2y4−5x3y2+5xy4 Thus, the answer is 2x4y2−2x2y4−5x3y2+5xy42x4y2-2x2y4-5x3y2+5xy4. 

Question 12: Multiply:

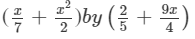
Answer 12: To multiply the expressions, we will use the distributive law in the following way: 

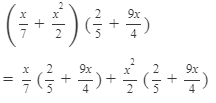
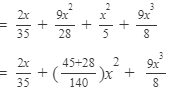
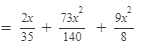
Thus, the answer is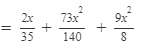 

Question 13: Multiply:

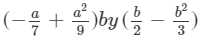
Answer 13: To multiply, we will use distributive law as follows: 

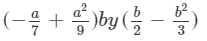
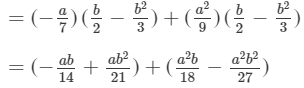
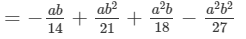
Thus, the answer is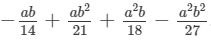 

Question 14: Multiply:

(3x²y − 5xy²) by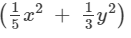 

Answer 14: To multiply, we will use distributive law as follows: 

(3x2y−5xy2) (1/5 x2+1/3 y2) 

= 1/5 x2(3x2y−5xy2)+1/3 y2(3x2y−5xy2) 

= 3/5 x4y−x3y2+x2y3−5/3 xy4 

Thus, the answer is 3/5 x4y−x3y2+x2y3−5/3 xy4 

Question 15: Multiply:
(2x² − 1) by (4x³ + 5x²)

Answer 15: To multiply, we will use distributive law as follows:
(2x2−1)(4x3+5x2)=2x2(4x3+5x2)−1(4x3+5x2)=8x5+10x4−4x3−5x2Thus, the answer is 8x5+10x4−4x3−5x28x5+10x4-4x3-5x2. 

Question 16: (2xy + 3y²) (3y² − 2)

Answer 16: To multiply, we will use distributive law as follows:
(2xy+3y2)(3y2−2)=2xy(3y2−2)+3y2(3y2−2)=6xy3−4xy+9y4−6y2=9y4+6xy3−6y2−4xyThus, the answer is 9y4+6xy3−6y2−4xy9y4+6xy3-6y2-4xy. 

Question 17: Find the following product and verify the result for x = − 1, y = − 2:
(3x − 5y) (x + y)

Answer 17: To multiply, we will use distributive law as follows:
(3x−5y)(x+y)=3x(x+y)−5y(x+y)=3x2+3xy−5xy−5y2=3x2−2xy−5y2∴∴ (3x−5y)(x+y)=3x2−2xy−5y23x-5yx+y=3x2-2xy-5y2. 

Now, we put x = −-1 and y = −-2 on both sides to verify the result.

LHS=(3x−5y)(x+y)={3(−1)−5(−2)}{−1+(−2)}=(−3+10)(−3)=(7)(−3)=−21 RHS=3x2−2xy−5y2=3(−1)2−2(−1)(−2)−5(−2)2=3×1−4−5×4=3−4−20=−21 Because LHS is equal to RHS, the result is verified.
Thus, the answer is 3x2−2xy−5y23x2-2xy-5y2.  

Question 18: Find the following product and verify the result for x = − 1, y = − 2:
(x²y − 1) (3 − 2x²y)

Answer 18: To multiply, we will  use distributive law as follows: 

(x2y−1)(3−2x2y)=x2y(3−2x2y)−1×(3−2x2y)=3x2y−2x4y2−3+2x2y=5x2y−2x4y2−3 ∴∴ (x2y−1)(3−2x2y)=5x2y−2x4y2−3x2y-13-2x2y=5x2y-2x4y2-3

Now, we put x = −-1 and y = −-2 on both sides to verify the result. 

LHS = (x2y−1)(3−2x2y)=[(−1)2(−2)−1][3−2(−1)2(−2)]=[1×(−2)−1][3−2×1×(−2)]=(−2−1)(3+4)=−3×7=−21RHS=5x2y−2x4y2−3=5(−1)2(−2)−2(−1)4(−2)2−3=[5×1×(−2)]−[2×1×4]−3=−10−8−3=−21  Because LHS is equal to RHS, the result is verified.
Thus, the answer is 5x2y−2x4y2−35x2y-2x4y2-3. 

Question 19: Find the following product and verify the result for x = − 1, y = − 2:

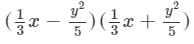
Answer 19: To multiply, we will use distributive law as follows:

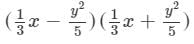
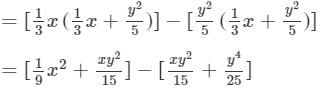
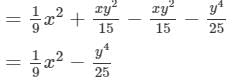
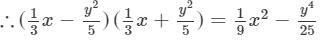
Now, we will put x = −-1 and y = −-2 on both the sides to verify the result. 

=- 119/225

RHS= 

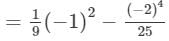
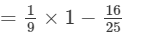
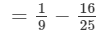
= - 119/225

Because LHS is equal to RHS, the result is verified. 

Thus, the answer is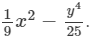 

Question 20: Simplify:
x²(x + 2y) (x − 3y)

Answer 20: To simplify, we will proceed as follows: 

x2(x+2y)(x−3y)=[x2(x+2y)](x−3y)=(x3+2x2y)(x−3y)=x3(x−3y)+2x2y(x−3y)=x4−3x3y+2x3y−6x2y2=x4−x3y−6x2y2 Thus, the answer is x4−x3y−6x2y2x4-x3y-6x2y2. 

Question 21: Simplify:
(x² − 2y²) (x + 4y) x²y²

Answer 21: To simplify, we will proceed as follows: 

(x2−2y2)(x+4y)x2y2=[x2(x+4y)−2y2(x+4y)]x2y2=(x3+4x2y−2xy2−8y3)x2y2=x5y2+4x4y3−2x3y4−8x2y5 Thus, the answer is x5y2+4x4y3−2x3y4−8x2y5x5y2+4x4y3-2x3y4-8x2y5. 

Question 22: Simplify:
a²b²(a + 2b)(3a + b)

Answer 22: To simplify, we will proceed as follows: 

a2b2(a+2b)(3a+b)=[a2b2(a+2b)](3a+b)=(a3b2+2a2b3)(3a+b)=3a(a3b2+2a2b3)+b(a3b2+2a2b3)=3a4b2+6a3b3+a