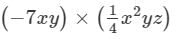RD Sharma Solutions for Class 8 Math Chapter 6 - Algebraic Expressions and Identities (Part-2) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Find each of the following product:
5x2 × 4x3
Answer 1: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices. However, use of these laws are subject to their applicability in the given expressions.
In the present problem, to perform the multiplication, we can proceed as follows:
5x2×4x3=(5×4)×(x2×x3)5x2×4x3=5×4×x2×x3
=20x5=20x5 (∵∵ am×an=am+nam×an=am+n)
Thus, the answer is 20x520x5.
Question 2: Find each of the following product:
−3a2 × 4b4
Answer 2: To multiply algebraic expressions, we can use commutative and associative laws along with the law of indices, am×an=am+nam×an=am+n, wherever applicable.
We have:
−3a2×4b4=(−3×4)×(a2×b4)=−12a2b4-3a2×4b4=-3×4×a2×b4=-12a2Thus, the answer is −12a2b4-12a2b4.
Question 3: Find each of the following product:
(−5xy) × (−3x2yz)
Answer 3: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, am×an=am+nam×an=am+n, wherever applicable.
We have:
(−5xy)×(−3x2yz)={(−5)×(−3)}× (x×x2)×(y×y)×z=15× (x1+2)×(y1+1)×z=15x3y2z-5xy×-3x2yz=-5×-3× x×x2×y×y×z=15× x1+2×y1+1×z=15x3y2Thus, the answer is 15x3y2z15x3y2z.
Question 4: Find each of the following product:
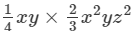
Answer 4: To multiply algebraic expressions, we use commutative and associative laws along with the the law of indices, that is, am×an=am+nam×an=am+n.
We have:
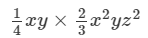
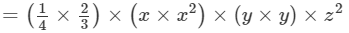
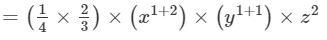
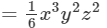
Thus, the answer is 1/6 x3y2z216x3y2z2.
Question 5: Find each of the following product:
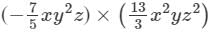
Answer 5: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
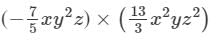
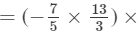 (x×x2)×(y2×y)×(z×z2)
(x×x2)×(y2×y)×(z×z2)
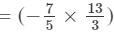 ×(x1+2)×(y2+1)×(z1+2)
×(x1+2)×(y2+1)×(z1+2)
= - 91/15 x3y3x3
Thus, the answer is = - 91/15 x3y3x3
Question 6: Find each of the following product:
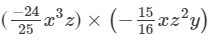
Answer 6: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
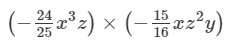
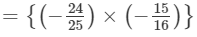 ×(x3×x)×(z×z2)×y
×(x3×x)×(z×z2)×y
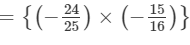 ×(x3+1)×(z1+2)×y
×(x3+1)×(z1+2)×y
= 9/10 x4yz3=910x4yz3
Thus, the answer is 9/10 x4yz3=910x4yz3
Question 7: Find each of the following product:
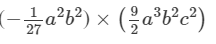
Answer 7:To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
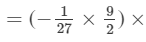 (a2×a3)×(b2×b2)×c2
(a2×a3)×(b2×b2)×c2
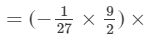 (a2+3)×(b2+2)×c2
(a2+3)×(b2+2)×c2
= - 1/6 a5b4c2
Thus, the answer is = - 1/6 a5b4c2
Question 8: Find each of the following product:
Answer 8: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
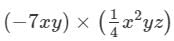
=(−7×1/4)×(x×x2)×(y×y)×z
=(−7×1/4)×(x1+2)×(y1+1)×z
=− 7/4 x3y2z
Thus, the answer is − 7/4 x3y2z
Question 9: Find each of the following product:
(7ab) × (−5ab2c) × (6abc2)
Answer 9: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have: (7ab)×(−5ab2c)×(6abc2)={7×(−5)×6}×(a×a×a)×(b×b2×b)×(c×c2)={7×(−5)×6}×(a1+1+1)×(b1+2+1)×(c1+2)=−210a3b4c3 Thus, the answer is −210a3b4c3-210a3b4c3.
Question 10: Find each of the following product:
(−5a) × (−10a2) × (−2a3)
Answer 10: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
(−5a)×(−10a2)×(−2a3)={(−5)×(−10)×(−2)}×(a×a2×a3)={(−5)×(−10)×(−2)}×(a1+2+3)=−100a6Thus, the answer is −100a6-100a6.
Question 11: Find each of the following product:
(−4x2) × (−6xy2) × (−3yz2)
Answer 11: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
(−4x2)×(−6xy2)×(−3yz2)={(−4)×(−6)×(−3)}×(x2×x)×(y2×y)×z2={(−4)×(−6)×(−3)}×(x2+1)×(y2+1)×z2=−72x3y3z2Thus, the answer is −72x3y3z2-72x3y3z2.
Question 12: Find each of the following product:
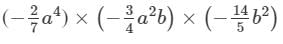
Answer 12: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
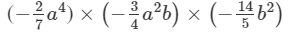
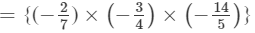 ×(a4×a2)×(b×b2)
×(a4×a2)×(b×b2)
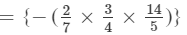 ×a4+2×b1+2
×a4+2×b1+2
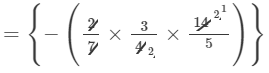 ×a6×b3
×a6×b3
=− 3/5 a6b3
Thus, the answer is − 3/5 a6b3
Question 13: Find each of the following product:
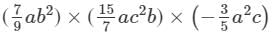
Answer 13: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
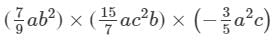
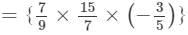 ×(a×a×a2)×(b2×b)×(c2×c)
×(a×a×a2)×(b2×b)×(c2×c)
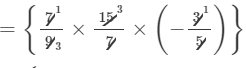 ×(a×a×a2)×(b2×b)×(c2×c)
×(a×a×a2)×(b2×b)×(c2×c)
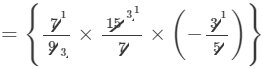 ×(a1+1+2)×(b2+1)×(c2+1)
×(a1+1+2)×(b2+1)×(c2+1)
=−a4b3c3
Thus, the answer is −a4b3c3-a4b3c3.
Question 14: Find each of the following product:
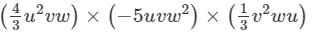
Answer 14: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e.,am×an=am+nam×an=am+n.
We have:
(4/3 u2vw)×(−5uvw2)×(1/3 v2wu)
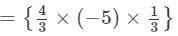 ×(u2×u×u)×(v×v×v2)×(w×w2×w)
×(u2×u×u)×(v×v×v2)×(w×w2×w)
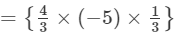 ×(u2+1+1)×(v1+1+2)×(w1+2+1)
×(u2+1+1)×(v1+1+2)×(w1+2+1)
=− 20/9 u4v4w4
Thus, the answer is − 20/9 u4v4w4
Question 15: Find each of the following product:
(0.5x)×(1/3 xy2z4)×(24x2yz)0.5x×13xy2z4×24x2yz
Answer 15: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
(0.5x)×(1/3 xy2z4)×(24x2yz)
=(0.5×1/3×24)×(x×x×x2)×(y2×y)×(z4×z)
=(0.5×1/3×24)×(x1+1+2)×(y2+1)×(z4+1)
=4x4y3z5
Thus, the answer is 4x4y3z54x4y3z5.
Question 16: Find each of the following product:
(4/3 pq2)×(−1/4 p2r)×(16p2q2r2)43pq2×-14p2r×16p2q2r2
Answer 16: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
(4/3 pq2)×(−1/4 p2r)×(16p2q2r2)
={4/3×(−1/4)×16}×(p×p2×p2)×(q2×q2)×(r×r2)
={4/3×(− 1/4)×16}×(p1+2+2)×(q2+2)×(r1+2)
=− 16/3p5q4r3
Thus, the answer is −1/3 p5q4r3-13p5q4r3.
Question 17: Find each of the following product:
(2.3xy) × (0.1x) × (0.16)
Answer 17: To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
(2.3xy)×(0.1x)×(0.16)=(2.3×0.1×0.16)×(x×x)×y=(2.3×0.1×0.16)×(x1+1)×y=0.0368x2yThus, the answer is 0.0368x2y0.0368x2y.
Question 18: Express each of the following product as a monomials and verify the result in each case for x = 1:
(3x) × (4x) × (−5x)
Answer 18: We have to find the product of the expression in order to express it as a monomial.
To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
(3x)×(4x)×(−5x)={3×4×(−5)}×(x×x×x)={3×4×(−5)}×(x1+1+1)=−60x33x×4x×-5x=3×4×-5×x×x×x=3×4×-5×x1+1+1=-60x3
Substituting x = 1 in LHS, we get:
LHS =(3x)×(4x)×(−5x)=(3×1)×(4×1)×(−5×1)
=−60
Putting x = 1 in RHS, we get:
RHS =−60x3=−60(1)3=−60×1=−60∵∵ LHS = RHS for x = 1; therefore, the result is correct
Thus, the answer is −60x3-60x3.
Question 19: Express each of the following product as a monomials and verify the result in each case for x = 1:
(4x2) × (−3x) × (4/5 x3)
Answer 19: We have to find the product of the expression in order to express it as a monomial.
To multiply algebraic expressions, we use commutative and associative laws along with the law of indices, i.e., am×an=am+nam×an=am+n.
We have:
(4x2)×(−3x)×(4/5 x3)
={4×(−3)×4/5}×(x2×x×x3)
={4×(−3)×4/5}×(x2+1+3)
=− 48/5x6
∴∴ (4x2)×(−3x)×(4/5 x3)=− 48/5x6
Substituting x = 1 in LHS, we get:
LHS=(4x2)×(−3x)×(4/5 x3)
=(4×12)×(−3×1)×(4/5 ×13)
=4×(−3)×4/5
=−48/5
Putting x = 1 in RHS, we get:
RHS=− 48/5 x6
=−48/5×16
=−48/5
∵∵ LHS = RHS for x = 1; therefore, the result is correct
Thus, the answer is − 48/5 x6-485x6.
Question 20: Express each of the following product as a monomials and verify the result in each case for x = 1:
(5x4) × (x2)3 × (2x)2
Answer 20: We have to find the product of the expression in order to express it as a monomial.
To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e., am×an=am+n and (am)n=amn am×an=am+n and amn=amn .
We have:
(5x4)×(x2)3×(2x)2 =(5x4)×(x6)×(22×x2)=(5×22)×(x4×x6×x2)=(5×22)×(x4+6+2)=20x12∴ (5x4)×(x2)3×(2x)2 =20x12
Substituting x = 1 in LHS, we get:
LHS=(5x4)×(x2)3×(2x)2 =(5×14)×(12)3×(2×1)2 =(5×1)×(16)×(2)2 =5×1×4=20
Put x =1 in RHS, we getRHS =20x12=20×(1)12=20×1=20∵∵ LHS = RHS for x = 1; therefore, the result is correct.
Thus, the answer is 20x1220x12.
Question 21: Express each of the following product as a monomials and verify the result in each case for x = 1:
(x2)3 × (2x) × (−4x) × (5)
Answer 21: We have to find the product of the expression in order to express it as a monomial.
To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e.,am×an=am+n and (am)n=amn am×an=am+n and amn=amn .
We have:
(x2)3×(2x)×(−4x)×5=(x6)×(2x)×(−4x)×5={2×(−4)×5}×(x6×x×x)={2×(−4)×5}×(x6+1+1)=−40x8
∴∴ (x2)3×(2x)×(−4x)×5=−40x8x23×2x×-4x×5=-40x8
Substituting x = 1 in LHS, we get:
LHS =(x2)3×(2x)×(−4x)×5=(12)3×(2×1)×(−4×1)×5=16×2×(−4)×5=1×2×(−4)×5=−40 Putting x = 1 in RHS, we get:
RHS=−40x8=−40(1)8=−40×1=−40 ∵∵ LHS = RHS for x = 1; therefore, the result is correct
Thus, the answer is −40x8 .
Question 22: Write down the product of −8x2y6 and −20xy. Verify the product for x = 2.5, y = 1.
Answer 22: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e., am×an=am+nam×an=am+n.
We have:
(−8x2y6)×(−20xy)={(−8)×(−20)}×(x2×x)×(y6×y)={(−8)×(−20)}×(x2+1)×(y6+1)=−160x3y7 ∴∴ (−8x2y6)×(−20xy)=−160x3y7-8x2y6×-20xy=-160x3y7
Substituting x = 2.5 and y = 1 in LHS, we get:
LHS=(−8x2y6)×(−20xy)={−8(2.5)2(1)6}×{−20(2.5)(1)}={−8(6.25)(1)}×{−20(2.5)(1)}=(−50)×(−50)=2500 Substituting x = 2.5 and y = 1 in RHS, we get:
RHS=−160x3y7=−160(2.5)3(1)7=−160(15.625)×1=−2500 Because LHS is equal to RHS, the result is correct.
Thus, the answer is −160x3y7-160x3y7.
Question 23:Evaluate (3.2x6y3) × (2.1x2y2) when x = 1 and y = 0.5
Ans
First multiply the expressions and then substitute the values for the variables.
To multiply algebric experssions use the commutative and the associative laws along with the law of indices, am×an=am+nam×an=am+n.
We have,
(3.2x6y3)×(2.1x2y2)=(3.2×2.1)×(x6×x2)×(y3×y2)=6.72x8y53.2x6y3×2.1x2y2=3.2×2.1×x6×x2×y3×y2=6.72x8y5Hence, (3.2x6y3)×(2.1x2y2)=6.72x8y53.2x6y3×2.1x2y2=6.72x8y5
Now, substitute 1 for x and 0.5 for y in the result.
6.72x8y5
=6.72(1)8(0.5)5
=6.72×1×0.03125
=0.216.72x8y5=6.72180.55=6.72×1×0.03125=0.2Hence, the answer is 0.210.21.
Answer 23: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e., am×an=am+nam×an=am+n.
We have:
(3.2x6y3)×(2.1x2y2)=(3.2×2.1)×(x6×x2)×(y3×y2)=(3.2×2.1)×(x6+2)×(y3+2)=6.72x8y53.2x6y3×2.1x2y2=3.2×2.1×x6×x2×y3×y2=3.2×2.1×x6+2×y3+2=6.72x8y5
∴∴ (3.2x6y3)×(2.1x2y2)=6.72x8y53.2x6y3×2.1x2y2=6.72x8y5
Substituting x = 1 and y = 0.5 in the result, we get:
6.72x8y5
=6.72(1)8(0.5)5
=6.72×1×0.03125
=0.2172x8y5=6.72180.55=6.72×1×0.03125=0.21
Thus, the answer is 0.210.21.
Question 24: Find the value of (5x6) × (−1.5x2y3) × (−12xy2) when x = 1, y = 0.5.
Answer 24: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e., am×an=am+nam×an=am+n.
We have:
(5x6)×(−1.5x2y3)×(−12xy2)
={5×(−1.5)×(−12)}×(x6×x2×x)×(y3×y2)
=5×(−1.5)×(−12)×(x6+2+1)×(y3+2)
=90x9y5
Substituting x = 1 and y = 0.5 in the result, we get:
90x9y5=90(1)9(0.5)5=90×1×0.03125=2.812590x9y5=90190.55=90×1×0.03125=2.8125
Thus, the answer is 2.8125.
Question 25: Evaluate (2.3a5b2) × (1.2a2b2) when a = 1 and b = 0.5.
Answer 25: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e., am×an=am+nam×an=am+n.
We have:
(2.3a5b2)×(1.2a2b2)
=(2.3×1.2)×(a5×a2)×(b2×b2)
=(2.3×1.2)×(a5+2)×(b2+2)
=2.76a7b4
∴∴ (2.3a5b2)×(1.2a2b2)=2.76a7b4
Substituting a =1 and b = 0.5 in the result, we get:
2.76a7b4=2.76(1)7(0.5)4=2.76×1×0.0625=0.17252.76a7b4=2.76170.54=2.76×1×0.0625=0.1725
Thus, the answer is 0.17250.1725.
Question 26: Evaluate (−8x2y6) × (−20xy) for x = 2.5 and y = 1.
Answer 26: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e.,am×an=am+nam×an=am+n.
We have:
(−8x2y6)×(−20xy)={(−8)×(−20)}×(x2×x)×(y6×y)={(−8)×(−20)}×(x2+1)×(y6+1)=160x3y7-8x2y6×-20xy=-8×-20×x2×x×y6×y=-8×-20×x2+1×y6+1=160x3y7
∴∴ (−8x2y6)×(−20xy)=160x3y7-8x2y6×-20xy=160x3y7
Substituting x = 2.5 and y = 1 in the result, we get:
160x3y7=160(2.5)3(1)7=160×15.625=2500160x3y7=1602.5317=160×15.625=2500
Thus, the answer is 25002500.
Question 27: Express each of the following product as a monomials and verify the result for x = 1, y = 2:
(−xy3) × (yx3) × (xy)
Answer 27: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e.,am×an=am+nam×an=am+n.
We have:
(−xy3)×(yx3)×(xy)=(−1)×(x×x3×x)×(y3×y×y)=(−1)×(x1+3+1)×(y3+1+1)=−x5y5-xy3×yx3×xy=-1×x×x3×x×y3×y×y=-1×x1+3+1×y3+1+1=-x5y5
To verify the result, we substitute x = 1 and y = 2 in LHS; we get:
LHS =(−xy3)×(yx3)×(xy)={(−1)×1×23}×(2×13)×(1×2)={(−1)×1×8}×(2×1)×2=(−8)×2×2=−32LHS =-xy3×yx3×xy=-1×1×23×2×13×1×2=-1×1×8×2×1×2=-8×2×2=-32
Substituting x = 1 and y = 2 in RHS, we get:
RHS=−x5y5=(−1)(1)5(2)5=(−1)×1×32=−32RHS=-x5y5=-11525=-1×1×32=-32
Because LHS is equal to RHS, the result is correct.
Thus, the answer is −x5y5-x5y5.
Question 28: Express each of the following product as a monomials and verify the result for x = 1, y = 2:
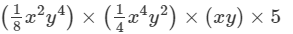
Answer 28: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e., am×an=am+nam×an=am+n.
We have:
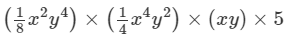
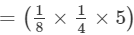 ×(x2×x4×x)×(y4×y2×y)
×(x2×x4×x)×(y4×y2×y)
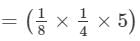 ×(x2+4+1)×(y4+2+1)
×(x2+4+1)×(y4+2+1)
= 5/32 x7y7
To verify the result, we substitute x = 1 and y = 2 in LHS; we get:
LHS= 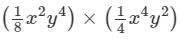 ×(xy)×5
×(xy)×5
={1/8×(1)2×(2)4}×{1/4×(1)4×(2)2}×(1×2)×5
=(1/8×1×16)×(1/4 ×1×4)×(1×2)×5
=2×1×2×5=20 Substituting x = 1 and y = 2 in RHS, we get:
RHS=5/32 x7y7
=5/32 (1)7(2)7
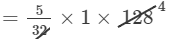
=20
Because LHS is equal to RHS, the result is correct.
Thus, the answer is 5/32 x7y7532x7y7.
Question 29: Express each of the following product as a monomials and verify the result for x = 1, y = 2:
(2/5 a2b)×(−15b2ac)×(−1/2 c2)25a2b×-15b2ac×-12c2
Answer 29: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e., am×an=am+nam×an=am+n.
We have:
(2/5 a2b)×(−15b2ac)×(−1/2 c2)
={2/5 ×(−15)×(−1/2)}×(a2×a)×(b×b2)×(c×c2)
={2/5 ×(−15)×(−1/2)}×(a2+1)×(b1+2)×(c1+2)
=3a3b3c3
∵∵ The expression doesn't consist of the variables x and y.
∴∴ The result cannot be verified for x = 1 and y = 2
Thus, the answer is 3a3b3c33a3b3c3.
Question 30: Express each of the following product as a monomials and verify the result for x = 1, y = 2:
(−4/7 a2b)×(−2/3 b2c)×(−7/6 c2a)-47a2b×-23b2c×-76c2a
Answer 30: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e., am×an=am+nam×an=am+n.
We have:
(−4/7 a2b)×(−2/3 b2c)×(−7/6 c2a)
={(−4/7)×(−2/3)×(−7/6)}×(a2×a)×(b×b2)×(c×c2)
={(−4/7)×(−2/3)×(−7/6)}×(a2+1)×(b1+2)×(c1+2)
=−4/9a3b3c3
∵∵ The expression doesn't consist of the variables x and y.
∴∴ The result cannot be verified for x = 1 and y = 2.
Thus, the answer is −4/9a3b3c3-49a3b3c3.
Question 31: Express each of the following product as a monomials and verify the result for x = 1, y = 2:
(4/9 abc3)×(−27/5a3b2)×(−8b3c)49abc3×-275a3b2×-8b3c
Answer 31: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e., am×an=am+nam×an=am+n.
We have:
(4/9 abc3)×(−27/5 a3b2)×(−8b3c)
={(4/9)×(−27/5)×(−8)}×(a×a3)×(b×b2×b3)×(c3×c)
={(4/9)×(−27/5)×(−8)}×(a1+3)×(b1+2+3)×(c3+1)
=96/5 a4b6c4
Thus, the answer is 96/5 a4b6c4965a4b6c4.
∵∵ The expression doesn't consist of the variables x and y.
∴∴ The result cannot be verified for x = 1 and y = 2
Question 32: Evaluate each of the following when x = 2, y = −1.
(2xy)×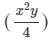 ×(x2)×(y2)(2xy)×x2y4×x2×y2
×(x2)×(y2)(2xy)×x2y4×x2×y2
Answer 32: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e., am×an=am+nam×an=am+n.
We have:
(2xy)×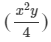 ×(x2)×(y2)
×(x2)×(y2)
=(2×1/4)×(x×x2×x2)×(y×y×y2)
(2×1/4)×(x1+2+2)×(y1+1+2)
=1/2 x5y4
∴∴ (2xy)×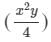 ×(x2)×(y2)=12x5y42xy×x2y4×x2×y2=12x5y4
×(x2)×(y2)=12x5y42xy×x2y4×x2×y2=12x5y4
Substituting x = 2 and y = −-1 in the result, we get:
1/2 x5y4
=1/2 (2)5(−1)4
=1/2×32×1
= 16
Thus, the answer is 1616.
Question 33: Evaluate each of the following when x = 2, y = −1.
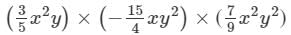
Answer 33: To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e., am×an=am+nam×an=am+n.
We have:
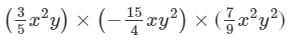
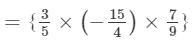 ×(x2×x×x2)×(y×y2×y2)
×(x2×x×x2)×(y×y2×y2)
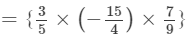 ×(x2+1+2)×(y1+2+2)
×(x2+1+2)×(y1+2+2)
=− 7/4 x5y5
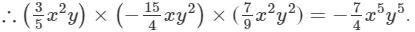
Substituting x = 2 and y = −-1 in the result, we get:
−7/4 x5y5
=−7/4 (2)5(−1)5
=(−7/4)×32×(−1)
= 56
Thus, the answer is 56. 2a3=-5×-10×-2×a×a2×a3=-5×-10×-2×a1+2+3=-100a6

|
Explore Courses for Class 8 exam
|

|