RD Sharma Solutions for Class 8 Math Chapter 8 - Division of Algebraic Expressions (Part-2) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Divide x + 2x2 + 3x4 − x5 by 2x.
Answer 1:
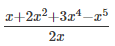
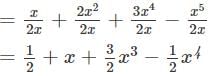
Question 2: Divide y4−3y3+1/2 y2 by 3yy4-3y3+12y2 by 3y.
Answer 2:
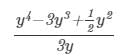
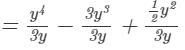
Question 3: Divide −4a3 + 4a2 + a by 2a.
Answer 3:
=−2a2+2a+1/2
Question 4: Divide −x6+2x4+4x3+2x2 by
Answer 4:
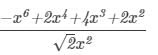
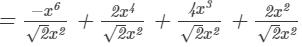
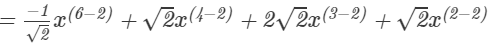
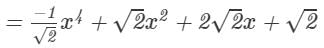
Question 5: Divide 5z3 − 6z2 + 7z by 2z.
Answer 5:
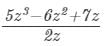
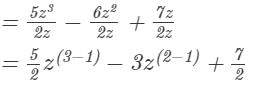
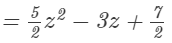
Question 6: Divide 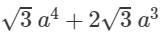 +3a2−6a by 3a3 a4+23 a3+3a2-6a by 3a.
+3a2−6a by 3a3 a4+23 a3+3a2-6a by 3a.
Answer 6: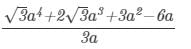
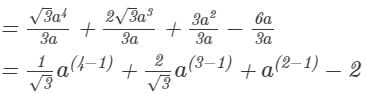
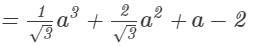
Question 7: Divide 5x3 − 15x2 + 25x by 5x.
Answer 7:
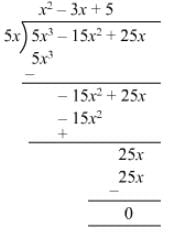
Question 8: Divide 4z3 + 6z2 − z by −1/2 12z.
Answer 8:
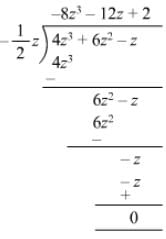
Question 9: Divide 9x2y − 6xy + 12xy2 by −3/2 32xy.
Answer 9:
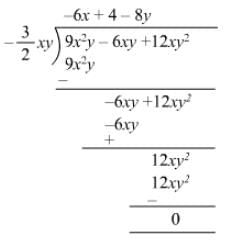
Question 10: Divide 3x3y2 + 2x2y + 15xy by 3xy.
Answer 10:
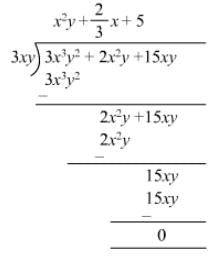
Question 11: Divide x2 + 7x + 12 by x + 4.
Answer 11:
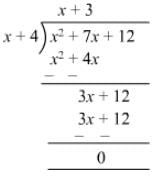
Question 12: Divide 4y2 + 3y + 1/212 by 2y + 1.
Answer 12:
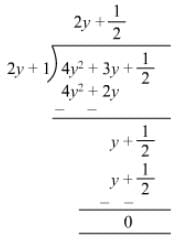
Question 13: Divide 3x3 + 4x2 + 5x + 18 by x + 2.
Answer 13:
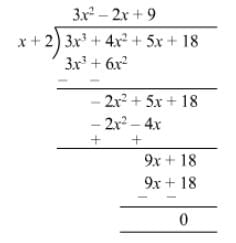
Question 14: Divide 14x2 − 53x + 45 by 7x − 9.
Answer 14:
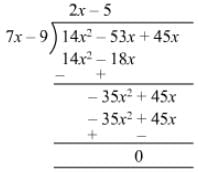
Question 15: Divide −21 + 71x − 31x2 − 24x3 by 3 − 8x.
Answer 15:
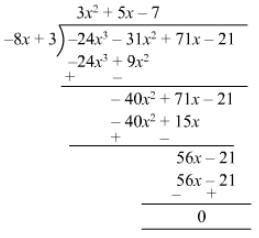
Question 16: Divide 3y4 − 3y3 − 4y2 − 4y by y2 − 2y.
Answer 16:

Question 17: Divide 2y5 + 10y4 + 6y3 + y2 + 5y + 3 by 2y3 + 1.
Answer 17:
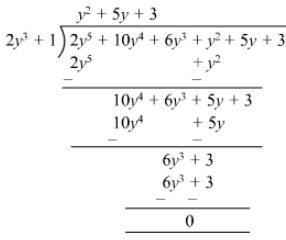
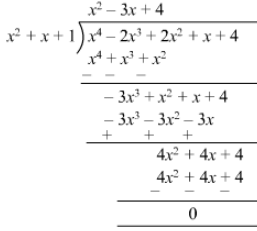
Question 18: Divide x4 − 2x3 + 2x2 + x + 4 by x2 + x + 1.
Answer 18:
Question 19: Divide m3 − 14m2 + 37m − 26 by m2 − 12m +13.
Answer 19:

Question 20: Divide x4 + x2 + 1 by x2 + x + 1.
Answer 20:
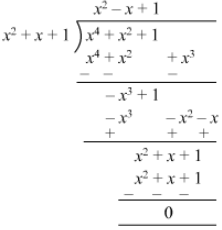
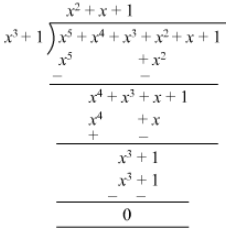
Question 21: Divide x5 + x4 + x3 + x2 + x + 1 by x3 + 1.
Answer 21:
Question 22: Divide 14x3 − 5x2 + 9x − 1 by 2x − 1 and find the quotient and remainder
Answer 22:
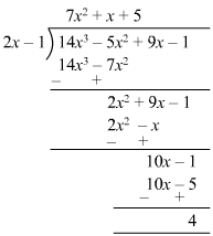 Quotient = 7x2 + x + 5Remainder = 4
Quotient = 7x2 + x + 5Remainder = 4
Question 23: Divide 6x3 − x2 − 10x − 3 by 2x − 3 and find the quotient and remainder.
Answer 23:
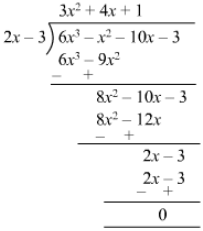
Quotient = 3x2+ 4x + 1 Remainder = 0Question 24: Divide 6x3 + 11x2 − 39x − 65 by 3x2 + 13x + 13 and find the quotient and remainder.
Answer 24:
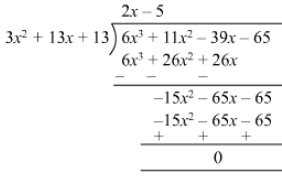
Quotient = 2x−5Remainder =0
Question 25: Divide 30x4 + 11x3 − 82x2 − 12x + 48 by 3x2 + 2x − 4 and find the quotient and remainder.
Answer 25: Quotient =10x2−3x−12
Remainder= 0

Question 26: Divide 9x4 − 4x2 + 4 by 3x2 − 4x + 2 and find the quotient and remainder.
Answer 26:

∴∴ Quotient = 3x2 + 4x + 2 and remainder = 0.
Question 27: Verify the division algorithm i.e. Dividend = Divisor × Quotient + Remainder, in each of the following. Also, write the quotient and remainder.
| Dividend | Divisor |
| 14x2 + 13x − 15 | 7x − 4 |
| 15z3 − 20z2 + 13z − 12 | 3z − 6 |
| 6y5 − 28y3 + 3y2 + 30y − 9 | 2y2 − 6 |
| 34x − 22x3 − 12x4 − 10x2 − 75 | 3x + 7 |
| 15y4 − 16y3 + 9y2 − 10/3 103y + 6 | 3y − 2 |
| 4y3 + 8y + 8y2 + 7 | 2y2 − y + 1 |
| 6y5 + 4y4 + 4y3 + 7y2 + 27y + 6 | 2y3 + 1 |
Answer 27: (i)
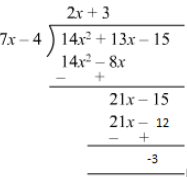
Quotient = 2x + 3
Remainder = −-3
Divisor = 7x −- 4
Divisor ×× Quotient + Remainder = (7x −- 4) (2x + 3) −- 3
= 14x2 + 21x −- 8x −- 12 −- 3
= 14x2 + 13x −- 15
= Dividend
Thus,
Divisor ×× Quotient + Remainder = Dividend
Hence verified.
(ii)
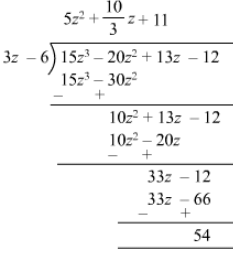
Quotient = 5z2+10/3 z+11Remainder = 54Divisor = 3z−6Divisor × Quotient +Remainder = (3z−6)( 5z2+10/3 z+11)+54= 15z3+10z2+33z−30z2−20z−66+54
= 15z3−20z2+13z−12
= Dividend
Thus,Divisor × Quotient + Remainder = DividendHence verified.
(iii)
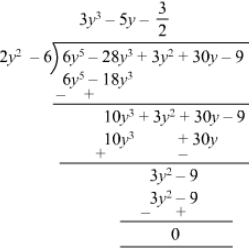
Quotient = 3y3−5y+323y3-5y+32
Remainder = 0
Divisor = 2y2 −- 6
Divisor ×× Quotient + Remainder =
(2y2−6) (3y3−5y+32)+0=6y5−10y3+3y2−18y3+30y−9=6y5−28 y3+3y2+30y−9 = Dividend
Thus, Divisor ×× Quotient + Remainder = Dividend
Hence verified.
(iv) 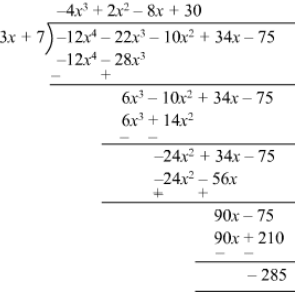
Quotient = −- 4x3 + 2x2 −- 8x + 30
Remainder = −- 285
Divisor = 3x + 7
Divisor ×× Quotient + Remainder = (3x + 7) (−- 4x3 + 2x2 −- 8x + 30) −- 285
= −- 12x4 + 6x3 −- 24x2 + 90x −- 28x3 + 14x2 −- 56x + 210 −- 285
= −- 12x 4 −- 22x3 −- 10x2 + 34x −- 75
= Dividend
Thus,
Divisor ×× Quotient + Remainder = Dividend
Hence verified.
(v) 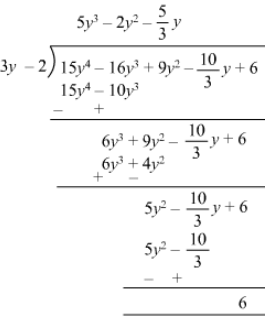
Quotient = 5y3−2y2+5/3 y5y3-2y2+53y
Remainder = 6
Divisor = 3y −- 2
Divisor ×× Quotient + Remainder = (3y −- 2) (5y3 −- 2y2 + 5/3 y53y) + 6
= 15y4−6y3+5y2−10y3+4y2−10/3 y+615y4-6y3+5y2-10y3+4y2-103y+6
= 15y4−16y3+9y2−10/3 y+615y4-16y3+9y2-103y+6
= Dividend
Thus,
Divisor ×× Quotient + Remainder = Dividend
Hence verified.
(vi) 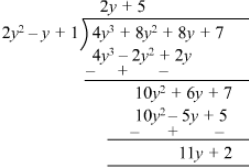
Quotient = 2y + 5
Remainder = 11y + 2
Divisor = 2y2 −- y + 1
Divisor ×× Quotient + Remainder = (2y2 −- y + 1) (2y + 5) + 11y + 2
= 4y3 +10y2 −- 2y2 −- 5y + 2y + 5 + 11y + 2
= 4y3 + 8y2 + 8y + 7
= Dividend
Thus,
Divisor ×× Quotient + Remainder = Dividend
Hence verified.
(vii) 
Quotient = 3y2 + 2y + 2
Remainder = 4y2 + 25y + 4
Divisor = 2y3 + 1
Divisor ×× Quotient + Remainder = (2y3 + 1) (3y2 + 2y + 2) + 4y2 + 25y + 4
= 6y5 + 4y4 + 4y3 + 3y2 + 2y + 2 + 4y2 + 25y + 4
= 6y5 + 4y4 + 4y3 + 7y2 + 27y + 6
= Dividend
Thus,
Divisor ×× Quotient + Remainder = Dividend
Hence verified.
Question 28: Divide 15y4 + 16y3 + 10/3 103y − 9y2 − 6 by 3y − 2. Write down the coefficients of the terms in the quotient.
Answer 28:

∴∴ Quotient = 5y3 + (26/3)y2 + (25/9)y + (80/27)
Remainder = (−- 2/27)
Coefficient of y3 = 5
Coefficient of y2 = (26/3)
Coefficient of y = (25/9)
Constant = (80/27)
Question 29: Using division of polynomials, state whether
(i) x + 6 is a factor of x2 − x − 42
(ii) 4x − 1 is a factor of 4x2 − 13x − 12
(iii) 2y − 5 is a factor of 4y4 − 10y3 − 10y2 + 30y − 15
(iv) 3y2 + 5 is a factor of 6y5 + 15y4 + 16y3 + 4y2 + 10y − 35
(v) z2 + 3 is a factor of z5 − 9z
(vi) 2x2 − x + 3 is a factor of 6x5 − x4 + 4x3 − 5x2 − x − 15
Answer 29: (i)
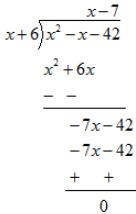
Remainder is zero. Hence (x+6) is a factor of x2 -x-42
(ii) 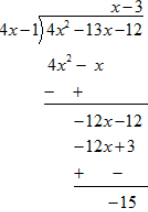
As the remainder is non zero . Hence ( 4x-1) is not a factor of 4x2 -13x-12
(iii) 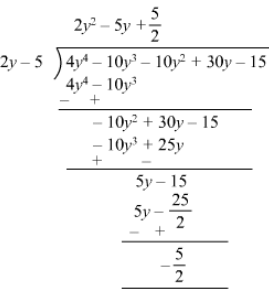
∵∵ The remainder is non zero,
2y −- 5 is not a factor of 4y4−10y3−10y2+30y−154y4-10y3-10y2+30y-15.
(iv)
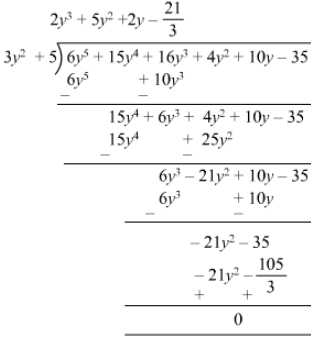
Remainder is zero. Therefore, 3y2 + 5 is a factor of 6y5+15y4+16y3+4y2+10y−356y5+15y4+16y3+4y2+10y-35.
(v) 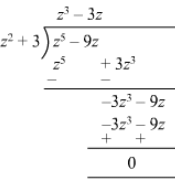
Remainder is zero; therefore, z2 + 3 is a factor of z5 −9zz5 -9z.
(vi) 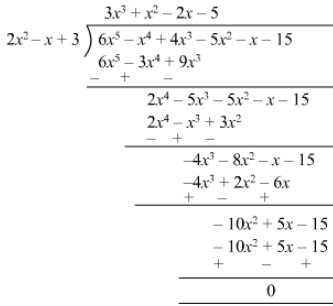
Remainder is zero ; therefore, 2x2−x+32x2-x+3 is a factor of 6x5−x4 +4x3−5x2−x−156x5-x4 +4x3-5x2-x-15.
Question 30: Find the value of a, if x + 2 is a factor of 4x4 + 2x3 − 3x2 + 8x + 5a.
Answer 30: We have to find the value of a if (x+2) is a factor of (4x4+2x3−3x2+8x+5a).Substituting x=−2 in 4x4+2x3−3x2+8x+5a, we get:4(−2)4+2(−2)3−3(−2)2+8(−2)+5a=0or, 64−16−12−16+5a=0or, 5a=−20or, a=−4∴ If (x+2) is a factor of (4x4+2x3−3x2+8x+5a), a=−4.Question 31: What must be added to x4 + 2x3 − 2x2 + x − 1 , so that the resulting polynomial is exactly divisible by x2 + 2x − 3?
Answer 31:
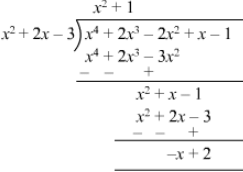
Thus, (x −- 2) should be added to (x4+2x3−2x2+x−1x4+2x3-2x2+x-1) to make the resulting polynomial exactly divisible by (x2+2x−3x2+2x-3).
FAQs on RD Sharma Solutions for Class 8 Math Chapter 8 - Division of Algebraic Expressions (Part-2) - RD Sharma Solutions for Class 8 Mathematics
| 1. What is the process of dividing algebraic expressions? |  |
| 2. Can we divide algebraic expressions with variables? |  |
| 3. What are the rules for dividing algebraic expressions? |  |
| 4. Can we divide algebraic expressions with different variables? |  |
| 5. How can I practice division of algebraic expressions? |  |
















