RS Aggarwal Solutions: Exercise 2D - Polynomials | Extra Documents & Tests for Class 9 PDF Download
Q.1. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = x3 – 8, g(x) = x – 2
Ans.
Let:
p(x) = x3 – 8
Now,
g(x) = 0 ⇒ x −2 = 0 ⇒ x =2
By the factor theorem, (x – 2) is a factor of the given polynomial if p(2) = 0.
Thus, we have:
p(2)=(23 − 8)=0
Hence, (x − 2) is a factor of the given polynomial.
Q.2. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 2x3 + 7x2 – 24x – 45, g(x) = x – 3
Ans.
Let:
p(x) = 2x3 + 7x2 – 24x – 45
Now,
x − 3 = 0 ⇒ x = 3
By the factor theorem, (x − 3) is a factor of the given polynomial if p(3) = 0.
Thus, we have:
p(3) = (2 × 33 − 7 × 32 − 24 × 3 − 45)
= (54 + 63 − 72 − 45)
= 0
Hence, (x − 3) is a factor of the given polynomial
Q.3. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 2x4 + 9x3 + 6x2 – 11x – 6, g(x) = x – 1
Ans.
Let:
p(x) = 2x4 + 9x3 + 6x2 – 11x – 6
Here,
x − 1 = 0 ⇒ x=1
By the factor theorem, (x − 1) is a factor of the given polynomial if p(1) = 0.
Thus, we have:
p(1)=(2×14 + 9 × 13 + 6 × 12 − 11 × 1 − 6)
= (2 + 9 + 6 − 11 −6)
= 0
Hence, (x − 1) is a factor of the given polynomial.
Q.4. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = x4 – x2 – 12, g(x) = x + 2
Ans.
Let:
p(x) = x4 – x2 – 12
Here,
x+2 = 0 ⇒ x= −2
By the factor theorem, (x + 2) is a factor of the given polynomial if p (−2) = 0.
Thus, we have:
p(−2) = [(−2)4 − (−2)2 − 12]
= (16 − 4 − 12)
=0
Hence, (x + 2) is a factor of the given polynomial.
Q.5. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 69 + 11x – x2 + x3, g(x) = x + 3
Ans.
p(x)=69+11x−x2+x3
g(x) = x + 3
Putting x = −3 in p(x), we get
p(−3) = 69 + 11 × (−3) − (−3)2 + (−3)3 = 69 − 33 − 9 − 27 = 0
Therefore, by factor theorem, (x + 3) is a factor of p(x).
Hence, g(x) is a factor of p(x).
Q.6. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 2x3 + 9x2 – 11x – 30, g(x) = x + 5
Ans.
Let:
p(x) = 2x3 + 9x2 − 11x − 30
Here,
x + 5 = 0 ⇒ x = −5
By the factor theorem, (x + 5) is a factor of the given polynomial if p (−5) = 0.
Thus, we have:
p(−5) = [2 × (−5)3 +9 × (−5)2 −11 × (−5)−30]
= (−250 + 225 + 55 − 30)
= 0
Hence, (x + 5) is a factor of the given polynomial.
Q.7. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 2x4 + x3 – 8x2 – x + 6, g(x) = 2x – 3
Ans.
Let:
p(x)=2x4 + x3 − 8x2 − x + 6
Here,
2x − 3 = 0 ⇒ x = 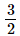
By the factor theorem, (2x − 3) is a factor of the given polynomial if p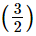 = 0
= 0
Thus, we have: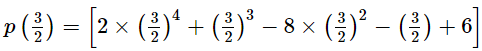
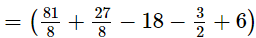
= 0
Hence, (2x − 3) is a factor of the given polynomial.
Q.8. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 3x3 + x2 – 20x + 12, g(x) = 3x – 2
Ans.
p(x) = 3x3 + x2 − 20x + 12
g(x) = 3x − 2 = 3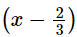
Putting 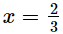 in p(x), we get
in p(x), we get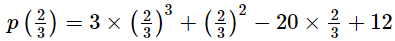
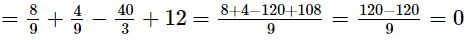
Therefore, by factor theorem, (3x − 2) is a factor of p(x).
Hence, g(x) is a factor of p(x).
Q.9. Using factor theorem, show that g(x) is a factor of p(x), when
p(x) = 7x2 −4√2x − 6, g(x) = x − √2
Ans.
Let:
p(x)=7x2−4√2x − 6
Here,
x−√2 = 0 ⇒ x = √2
By the factor theorem, (x - √2) is a factor of the given polynomial if p(√2)=0
Thus, we have:
p(√2) = [7×(√2)2 −4√2 × √2 −6]
=(14 − 8 − 6)
= 0
Hence, (x − √2) is a factor of the given polynomial.
Q.10. Using factor theorem, show that g(x) is a factor of p(x), when
p(x)=2√2x2 + 5x + √2, g(x) =x + √2
Ans.
Let:
p(x)=2√2x2 + 5x + √2
Here,
x + √2 = 0 ⇒ x = −√2
By the factor theorem, (x+√2) will be a factor of the given polynomial if p(−√2) = 0.
Thus, we have:
p(−√2) = [2√2 × (−√2)2 + 5 × (−√2)+√2]
=(4√2−5√2+√2)
= 0
Hence, (x + √2) is a factor of the given polynomial.
Q.11. Show that (p – 1) is a factor of (p10 – 1) and also of (p11 – 1).
Ans.
Let f(p) = p10 – 1 and g(p) = p11 – 1.
Putting p = 1 in f(p), we get
f(1) = 110 − 1 = 1 − 1 = 0
Therefore, by factor theorem, (p – 1) is a factor of (p10 – 1).
Now, putting p = 1 in g(p), we get
g(1) = 111 − 1 = 1 − 1 = 0
Therefore, by factor theorem, (p – 1) is a factor of (p11 – 1).
Q.12. Find the value of k for which (x − 1) is a factor of (2x3 + 9x2 + x + k).
Ans.
Let:
f(x)=2x3 + 9x2 + x + k
(x−1) is a factor of f(x) = 2x3 + 9x2 + x + k.
⇒ f(1) = 0
⇒2 × 13 + 9 × 12 + 1 + k = 0
⇒12 + k = 0
⇒k= −12
Hence, the required value of k is −12.
Q.13. Find the value of a for which (x − 4) is a factor of (2x3 − 3x2 − 18x + a).
Ans.
Let:
f(x)=2x3 − 3x2 − 18x + a
(x−4) is a factor of f(x)=2x3 − 3x2 − 18x + a.
⇒ f(4) = 0
⇒2 × 43 − 3 × 42 − 18 × 4 + a = 0
⇒8 + a = 0 ⇒ a = −8
Hence, the required value of a is −8.
Q.14. Find the value of a for which (x + 1) is a factor of (ax3 + x2 – 2x + 4a – 9).
Ans.
Let f(x) = ax3 + x2 – 2x + 4a – 9
It is given that (x + 1) is a factor of f(x).
Using factor theorem, we have
f(−1) = 0
⇒a×(−1)3+(−1)2−2×(−1) + 4a − 9 = 0
⇒− a + 1 + 2+ 4a −9 = 0
⇒ 3a −6 = 0
⇒ 3a = 6
⇒a = 2
Thus, the value of a is 2.
Q.15. Find the value of a for which (x + 2a) is a factor of (x5 – 4a2 x3 + 2x + 2a +3).
Ans.
Let f(x) = x5 – 4a2 x3 + 2x + 2a +3
It is given that (x + 2a) is a factor of f(x).
Using factor theorem, we have
f(−2a) = 0
⇒(−2a)5−4a2×(−2a)3+2×(−2a)+2a+3=0
⇒−32a5−4a2×(−8a3)+2×(−2a)+2a+3=0
⇒−32a5+32a5−4a+2a+3=0
⇒ −2a + 3 = 0
⇒ 2a = 3
⇒ 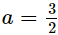
Thus, the value of a is 3/2.
Q.16. Find the value of m for which (2x – 1) is a factor of (8x4 + 4x3 – 16x2 + 10x + m).
Ans.
Let f(x) = 8x4 + 4x3 – 16x2 + 10x + m
It is given that (2x−1) = 2 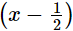 is a factor of f(x).
is a factor of f(x).
Using factor theorem, we have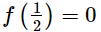
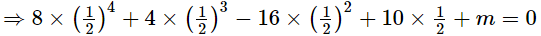
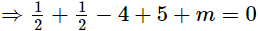
⇒2 + m = 0
⇒m = −2
Thus, the value of m is −2.
Q.17. Find the value of a for which the polynomial (x4 − x3 − 11x2 − x + a) is divisible by (x + 3).
Ans.
Let:
f(x) = x4 − x3 − 11x2 − x + a
Now,
x + 3 = 0 ⇒ x = −3
By the factor theorem, f(x) is exactly divisible by (x+3) if f (−3) = 0.
Thus, we have:
f(−3) = [(−3)4−(−3)3−11×(−3)2−(−3)+a]
=(81 + 27 − 99 + 3 + a)
=12 + a
Also,
f( − 3) = 0
⇒ 12 + a = 0
⇒ a = −12
Hence, f(x) is exactly divisible by (x+3) when a is −12.
Q.18. Without actual division, show that (x3 − 3x2 − 13x + 15) is exactly divisible by (x2 + 2x − 3).
Let:
f(x)=x3 − 3x2 −13 x + 15
And,
g(x) = x2 + 2x − 3
=x2 + x − 3x −3
=x(x − 1)+3(x − 1)
=(x − 1)(x + 3)
Now, f(x) will be exactly divisible by g(x) if it is exactly divisible by (x−1) as well as (x+3).
For this, we must have:
f(1) = 0 and f(−3) = 0
Thus, we have:
f(1) = (13 − 3 × 12 − 13 × 1 + 15)
=(1 − 3 − 13 + 15)
= 0
And,
f(−3)=[(−3)3−3×(−3)2−13×(−3)+15]
=(−27−27+39+15)
= 0
f(x) is exactly divisible by (x−1) as well as (x+3) . So, f(x) is exactly divisible by (x−1)(x+3).
Hence, f(x) is exactly divisible by x2 + 2x − 3.
Q.19. If (x3 + ax2 + bx + 6) has (x − 2) as a factor and leaves a remainder 3 when divided by (x − 3), find the values of a and b.
Ans.
Let:
f(x)=x3 + ax2 + bx + 6
(x−2) is a factor of f(x)=x3 + ax2 + bx + 6.
⇒f(2) = 0
⇒23 + a × 22 + b × 2 + 6 = 0
⇒14 + 4a + 2b =0
⇒4a + 2b = −14
⇒ 2a + b= −7 ...(1)
Now,
x − 3 = 0 ⇒ x = 3
By the factor theorem, we can say:
When f(x) will be divided by (x−3), 3 will be its remainder.
⇒ f(3) = 3
Now,
f(3)=33 + a × 32 + b × 3 + 6
=(27 + 9a + 3b + 6)
= 33 + 9a + 3b
Thus, we have:
f (3) = 3
⇒33 + 9a + 3b = 3
⇒9a + 3b = −30
⇒3a + b = −10 ...(2)
Subtracting (1) from (2), we get:
a = −3
By putting the value of a in (1), we get the value of b, i.e., −1.
∴ a = −3 and b = −1
Q.20. Find the values of a and b so that the polynomial (x3 − 10x2 + ax + b) is exactly divisible by (x −1) as well as (x − 2).
Ans.
Let:
f(x) =x3 − 10 x2 + ax + b
Now,
x − 1 = 0 ⇒ x = 1
By the factor theorem, we can say:
f(x) will be exactly divisible by (x − 1) if f(1) = 0
Thus, we have:
f(1)=13 − 10 × 12 + a × 1 + b
=(1 − 10 + a + b)
= −9 + a + b
∴ f(1) = 0 ⇒ a + b = 9 ...(1)
Also,
x − 2 = 0 ⇒ x = 2
By the factor theorem, we can say:
f(x) will be exactly divisible by (x−2) if f(2)=0.
Thus, we have:
f(2)=23 − 10 × 22 + a × 2 + b
=(8 − 40 + 2a + b)
= − 32 + 2a + b
∴ f(2) = 0 ⇒ 2a+b=32 ...(2)
Subtracting (1) from (2), we get:
a = 23
Putting the value of a, we get the value of b, i.e., −14.
∴ a = 23 and b = −14
Q.21. Find the values of a and b so that the polynomial (x4 + ax3 − 7x2 − 8x + b) is exactly divisible by (x + 2) as well as (x + 3).
Ans.
Let:
f(x)=x4 + ax3 − 7x2 − 8x + b
Now,
x + 2 = 0 ⇒ x = −2
By the factor theorem, we can say:
f(x) will be exactly divisible by (x+2) if f(−2)=0 .
Thus, we have:
f(−2)=[(−2)4+a×(−2)3−7×(−2)2−8×(−2)+b]
=(16 − 8a − 28 +16+ b)
=(4 − 8a + b)
∴ f(−2) = 0 ⇒ 8a − b = 4 ...(1)
Also,
x + 3 = 0 ⇒ x = −3
By the factor theorem, we can say:
f(x) will be exactly divisible by (x+3) if f(−3)=0 .Thus, we have:
f(−3) = [(−3)4+a×(−3)3−7×(−3)2−8×(−3)+b
=(81 −27a − 63 + 24 + b)
= (42 − 27 a + b)
∴ f(−3) = 0 ⇒ 27a − b = 42 ...(2)
Subtracting (1) from (2), we get:
⇒19a = 38
⇒ a = 2
Putting the value of a, we get the value of b, i.e., 12.
∴ a = 2 and b = 12
Q.22. If both (x – 2) and 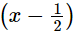 are factors of px2 + 5x + r, prove that p = r.
are factors of px2 + 5x + r, prove that p = r.
Ans.
Let f(x) = px2 + 5x + r
It is given that (x – 2) is a factor of f(x).
Using factor theorem, we have
f(2) = 0
⇒p × 22 + 5 × 2 + r = 0
⇒ 4p + r= −10 .....(1)
Also,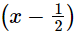 is a factor of f(x).
is a factor of f(x).
Using factor theorem, we have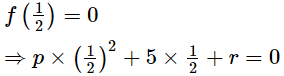
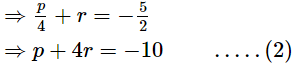
From (1) and (2), we have
4p + r = p + 4r
⇒ 4p − p= 4r − r
⇒3p = 3r
⇒ p = r
Q.23. Without actual division, prove that 2x4 – 5x3 + 2x2 – x + 2 is divisible by x2 – 3x + 2.
Ans.
Let f(x) = 2x4 – 5x3 + 2x2 – x + 2 and g(x) = x2 – 3x + 2.
x2 − 3x + 2
=x2 − 2x − x + 2
= x(x − 2) − 1(x − 2)
=(x−1)(x − 2)
Now, f(x) will be divisible by g(x) if f(x) is exactly divisible by both (x − 1) and (x − 2).
Putting x = 1 in f(x), we get
f(1) = 2 × 14 – 5 × 13 + 2 × 12 – 1 + 2 = 2 – 5 + 2 – 1 + 2 = 0
By factor theorem, (x − 1) is a factor of f(x). So, f(x) is exactly divisible by (x − 1).
Putting x = 2 in f(x), we get
f(2) = 2 × 24 – 5 × 23 + 2 × 22 – 2 + 2 = 32 – 40 + 8 – 2 + 2 = 0
By factor theorem, (x − 2) is a factor of f(x). So, f(x) is exactly divisible by (x − 2).
Thus, f(x) is exactly divisible by both (x − 1) and (x − 2).
Hence, f(x) = 2x4 – 5x3 + 2x2 – x + 2 is exactly divisible by (x − 1)(x − 2) = x2 – 3x + 2.
Q.24. What must be added to 2x4 – 5x3 + 2x2 – x – 3 so that the result is exactly divisible by (x – 2)?
Ans.
Let k be added to 2x4 – 5x3 + 2x2 – x – 3 so that the result is exactly divisible by (x – 2). Here, k is a constant.
∴ f(x) = 2x4 – 5x3 + 2x2 – x – 3 + k is exactly divisible by (x – 2).
Using factor theorem, we have
f(2)=0
⇒2×24−5×23+2×22−2−3+k=0
⇒32 − 40 + 8 − 5 + k = 0
⇒ −5 + k = 0
⇒k = 5
Thus, 5 must be added to 2x4 – 5x3 + 2x2 – x – 3 so that the result is exactly divisible by (x – 2).
Q.25. What must be subtracted from (x4 + 2x3 – 2x2 + 4x + 6) so that the result is exactly divisible by (x2 + 2x – 3)?
Ans.
Dividing (x4 + 2x3 – 2x2 + 4x + 6) by (x2 + 2x – 3) using long division method, we have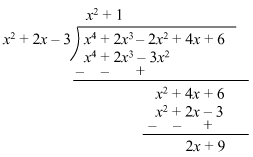
Here, the remainder obtained is (2x + 9).
Thus, the remainder (2x + 9) must be subtracted from (x4 + 2x3 – 2x2 + 4x + 6) so that the
result is exactly divisible by (x2 + 2x – 3).
Q.26. Use factor theorem to prove that (x + a) is a factor of (xn + an) for any odd positive integer.
Ans.
Let f(x) = xn + an
Putting x = −a in f(x), we get
f(−a) = (−a)n + an
If n is any odd positive integer, then
f(−a) = (−a)n + an = −an + an = 0
Therefore, by factor theorem, (x + a) is a factor of (xn + an) for any odd positive integer.
|
1 videos|228 docs|21 tests
|
FAQs on RS Aggarwal Solutions: Exercise 2D - Polynomials - Extra Documents & Tests for Class 9
| 1. What is a polynomial? |  |
| 2. How do you classify polynomials? |  |
| 3. What is the degree of a polynomial? |  |
| 4. Can a polynomial have negative exponents? |  |
| 5. What are the operations that can be performed on polynomials? |  |

|
Explore Courses for Class 9 exam
|

|

















