RS Aggarwal Solutions: Number System- 4 | Extra Documents & Tests for Class 9 PDF Download
Q.1. Add:
(i) (2√3 − 5√2) and (√3+2√2)
(ii) (2√2 + 5√3 − 7√5)and(3√3 − √2 + √5)
(iii)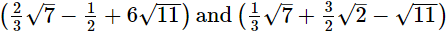
Ans.
(i) 2√3 − 5√2 + √ 3 + 2√2
= (2√3 + √3) + (2√2 − 5√2)
= 3√3− 3√2
(ii) 2√2+ 5√3 − 7√5 + 3√3 − √2 + √5
= 2√2 - √2 + 5√3 + 3√3 + √5 − 7√5
= √2 + 8√3 −6√5
(iii) 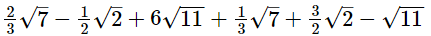
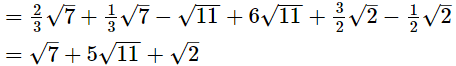
Q.2. Multiply:
(i) 3√5 by 2√5
(ii) 6√15 by 4√3
(iii) 2√6 by 3√3
(iv) 3√8 by 3√2
(v) √10 by √40
(vi) 3√28 by 2√7
Ans.
(i) 3√5 × 2√5 = 3 × 2 × √5 x √5 = 6 × 5 = 30
(ii) 6√15 × 4√3 = 6 × 4 × √5 × √3 × √3 = 24 × 3 × √5 = 72√5
(iii) 2√6 × 3√3 = 2 × 3 × √2 × √3 × √3 = 6 × 3 × √2 = 18√2
(iv) 3√8 × 3√2 = 3 × 3 × √2 × √2 × √2 × √2 = 9 × 4 = 36
(v) √10 × √40 = √2 × √5 × √2 × √2 × √2 × √5 = √2 × √2 × √2 × √2 × √5 × √5 = 2 × 2 × 5 = 20
(vi) 3√28 × 2√7 = 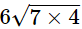 × √7 = 6 × 7 × √4 = 42 × 2 = 84
× √7 = 6 × 7 × √4 = 42 × 2 = 84
Q.3. Divide:
(i) 16√6 by 4√2
(ii) 12√5 by 4√3
(iii) 18√21 by 6√7
Ans.
(i) 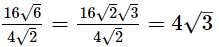
(ii)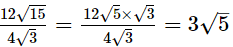
(iii)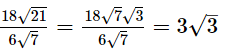
Q.4. Simplify
(i) (3 − √11) (3 + √11)
(ii) (−3 + √5) (−3 − √5)
(iii) (3 − √3)2
(iv) (√5 − √3)2
(v) (5 + √7) (2 + √5)
(vi) (√5 – √2) (√2 - √3)
Ans. (i) (3 − √11) (3 + √11)
=32 − (√11)2 [(a − b)( a + b) =a2 − b2]
=9 − 11
= −2
(ii) (−3 + √5) (−3 − √5)
=(−3)2−(√5)2 [(a + b)(a − b) = a2 − b2]
=9 − 5
=4
(iii) (3 − √3)2
=32+(√3)2 − 2 × 3 × √3 [(a−b)2=a2+b2−2ab]
=9 + 3 − 6√3
=12 − 6√3
(iv) (√5 − √3)2
=(√5)2+ (√3)2 − 2 × √5√3 [(a−b)2 = a2 + b2 − 2ab]
=5 + 3 − 2√15 = 8 − 2√15
= √5 × √2 − √5 × √3 - √2 × √2 + √2 × √3
= √10 − √15 − 2 + √6
(v) (5 + √7) (2 + √5)
(5 + √7) (2 + √5)
= 5 × 2 + 5 × √5+ √7 × 2 +√7 × √5
=10 + 5√5 + 2√7 + 3√5
(vi) (√5 − √2) (√2 − √3)
(√5 - √2)(√2 − √3)
= √5 × √2 – √5 × √3 − √2 × √2 + √2 × √3
= √10 − √15 − 2 + √6
Q.5. Simplify (3 + √3) (2 + √2)2.
Ans. (3 + √3) (2+√2)2
= (3 + √3) [22+(√2)2 + 2 × 2√2]
=(3 + √3) [4 + 2 + 4√2]
= (3 + √3) [6 + 4√2]
=3 × 6 + 3 × 4√2 + √3 × 6 + √3 × 4√2
=18 + 12√2 + 6√3 + 4√6
Q.6. Examine whether the following numbers are rational or irrational:
(i) (5 − √5) (5 + √5)
(ii) (√3 + 2)2
(iii)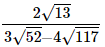
(iv) √8 + 4√32 − 6√2
Ans. (i) (5 − √5) (5 + √5)
=52 − (√5)2 [(a − b)(a + b) = a2 − b2]
= 25 − 5
= 20, which is an integer
Hence, (5 − √5) (5 + √5) is rational.
(ii) (√3 + 2)2
= (√3)2+22+2×√3×2 [(a + b)2=a2 + b2 + 2ab]
= 3 + 4 + 4√3
= 7 + 4√3
Since, the sum and product of rational numbers and an irrational number is always an irrational.
⇒7 + 4√3 is irrational.
Hence, (√3 + 2)2 is irrational.
(iii) 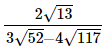
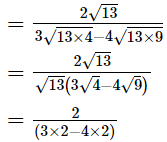
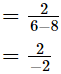
= −1, which is an integer
Hence, 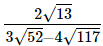 is rational.
is rational.
(iv) √8 + 4√32 −6√2
=2√2 + 4 × 4√2 − 6√2
=2√2 + 16√2 − 6√2
=12√2
Since, the product of a rational number and an irrational number is always an irrational.
Hence, √8 + 4√32 − 6√2 is rational.
Q.7. On her birthday Reema distributed chocolates in an orphanage. The total number of chocolates she distributed is given by (5+ √11) (5− √11).
(i) Find the number of chocolates distributed by her.
(ii) Write the moral values depicted here by Reema.
Ans.
(i) As, (5 + √11) (5 − √11)
=52−(√11)2 [(a+b)(a−b)=a2−b2]
=25 − 11
=14
Hence, the number of chocolates distributed by Reema is 14.
(ii) The moral values depicted here by Reema is helpfulness and caring.
Disclaimer: The moral values may vary from person to person.
Q.8. Simplify
(i) 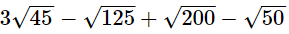
(ii) 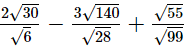
(iii) 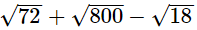
Ans.
(i) 3√45 − √125 + √200 − √50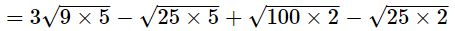
= 3×3√5 – 5√5 + 10√2 − 5√2
= 9√5 − 5√5 + 5√2
=4√5 + 5√2
(ii) 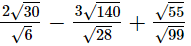
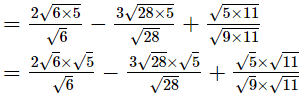
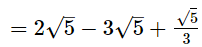
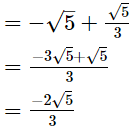
(iii) 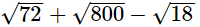
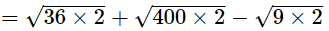
= 6√2 + 20√2 − 3√2
= 23√2
|
1 videos|228 docs|21 tests
|

|
Explore Courses for Class 9 exam
|

|

















