RS Aggarwal Solutions: Polynomials- 1 | Mathematics (Maths) Class 9 PDF Download
RS Aggarwal Solutions: Exercise 2A - Polynomials
Q.1. Which of the following expressions are polynomials? In case of a polynomial, write its degree.
(i) x5 − 2x3 + x + √3
(ii) y3 + √3y
(iii)
(iv) x100 − 1
(v)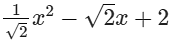
(vi) x−2 + 2x−1 + 3
(vii) 1
(viii)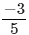
(ix)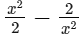
(x)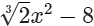
(xi)
(xii)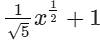
(xiii)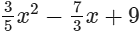
(xiv)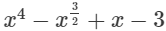
(xv) 2x3 + 3x2 + √x − 1
Ans.
(i) x5 − 2x3 + x +√3 is an expression having only non-negative integral powers of x. So, it is a polynomial. Also, the highest power of x is 5, so, it is a polynomial of degree 5.
(ii) y3 + √3y is an expression having only non-negative integral powers of y. So, it is a polynomial. Also, the highest power of y is 3, so, it is a polynomial of degree 3.
(iii)  is an expression having only non-negative integral powers of t. So, it is a polynomial. Also, the highest power of t is 2, so, it is a polynomial of degree 2.
is an expression having only non-negative integral powers of t. So, it is a polynomial. Also, the highest power of t is 2, so, it is a polynomial of degree 2.
(iv) x100 − 1 is an expression having only non-negative integral power of x. So, it is a polynomial. Also, the highest power of x is 100, so, it is a polynomial of degree 100.
(v) 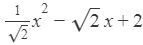 is an expression having only non-negative integral powers of x. So, it is a polynomial. Also, the highest power of x is 2, so, it is a polynomial of degree 2.
is an expression having only non-negative integral powers of x. So, it is a polynomial. Also, the highest power of x is 2, so, it is a polynomial of degree 2.
(vi) x−2+2x−1 + 3 is an expression having negative integral powers of x. So, it is not a polynomial.
(vii) Clearly, 1 is a constant polynomial of degree 0.
(viii) Clearly,  is a constant polynomial of degree 0.
is a constant polynomial of degree 0.
(ix) 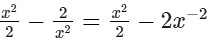
This is an expression having negative integral power of x i.e. −2. So, it is not a polynomial.
(x) is an expression having only non-negative integral power of x. So, it is a polynomial. Also, the highest power of x is 2, so, it is a polynomial of degree 2.
is an expression having only non-negative integral power of x. So, it is a polynomial. Also, the highest power of x is 2, so, it is a polynomial of degree 2.
(xi) is an expression having negative integral power of x. So, it is not a polynomial.
is an expression having negative integral power of x. So, it is not a polynomial.
(xii) 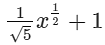
In this expression, the power of x is 1/2 which is a fraction. Since it is an expression having fractional power of x, so, it is not a polynomial.
(xiii) 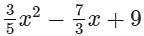 is an expression having only non-negative integral powers of x. So, it is a polynomial. Also, the highest power of x is 2, so, it is a polynomial of degree 2.
is an expression having only non-negative integral powers of x. So, it is a polynomial. Also, the highest power of x is 2, so, it is a polynomial of degree 2.
(xiv) 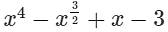
In this expression, one of the powers of x is 3/2 which is a fraction. Since it is an expression having fractional power of x, so, it is not a polynomial.
(xv)
In this expression, one of the powers of x is 1/2 which is a fraction. Since it is an expression having fractional power of x, so, it is not a polynomial.
Q.2. Identify constant, linear, quadratic, cubic and quartic polynomials from the following.
(i) –7 + x
(ii) 6y
(iii) –z3
(iv) 1 – y – y3
(v) x – x3 + x4
(vi) 1 + x + x2
(vii) – 6x2
(viii) – 13
(ix) – p
Ans.
(i) –7 + x is a polynomial with degree 1. So, it is a linear polynomial.
(ii) 6y is a polynomial with degree 1. So, it is a linear polynomial.
(iii) –z3 is a polynomial with degree 3. So, it is a cubic polynomial.
(iv) 1 – y – y3 is a polynomial with degree 3. So, it is a cubic polynomial.
(v) x – x3 + x4 is a polynomial with degree 4. So, it is a quartic polynomial.
(vi) 1 + x + x2 is a polynomial with degree 2. So, it is a quadratic polynomial.
(vii) – 6x2 is a polynomial with degree 2. So, it is a quadratic polynomial.
(viii) –13 is a polynomial with degree 0. So, it is a constant polynomial.
(ix) – p is a polynomial with degree 1. So, it is a linear polynomial.
Q.3. Write
(i) the coefficient of x3 in x+3x2 − 5x3 + x4.
(ii) the coefficient of x in √3−2√2x + 6x2.
(iii) the coefficient of x2 in 2x – 3 + x3.
(iv) the coefficient of x in 
(v) the constant term in
Ans.
(i) The coefficient of x3 in x+3x2−5x3 + x4 is − 5.
(ii) The coefficient of x in √3 − 2√2x + 6x2 is −2√2.
(iii) 2x – 3 + x3 = – 3 + 2x + 0x2 + x3
The coefficient of x2 in 2x – 3 + x3 is 0.
(iv) The coefficient of x in 
(v) The constant term in 
Q.4. Determine the degree of each of the following polynomials.
(i) 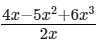
(ii) y2(y – y3)
(iii) (3x – 2) (2x3 + 3x2)
(iv)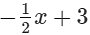
(v) – 8
(vi) x–2(x4 + x2)
Ans.
(i) 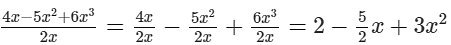
Here, the highest power of x is 2. So, the degree of the polynomial is 2.
(ii) y2(y – y3) = y3 – y5
Here, the highest power of y is 5. So, the degree of the polynomial is 5.
(iii) (3x – 2)(2x3 + 3x2) = 6x4 + 9x3 – 4x3 – 6x2 = 6x4 + 5x3 – 6x2
Here, the highest power of x is 4. So, the degree of the polynomial is 4.
(iv) 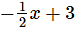
Here, the highest power of x is 1. So, the degree of the polynomial is 1.
(v) – 8
–8 is a constant polynomial. So, the degree of the polynomial is 0.
(vi) x–2(x4 + x2) = x2 + x0 = x2 + 1
Here, the highest power of x is 2. So, the degree of the polynomial is 2
Q.5.
(i) Give an example of a monomial of degree 5.
(ii) Give an example of a binomial of degree 8.
(iii) Give an example of a trinomial of degree 4.
(iv) Give an example of a monomial of degree 0.
Ans.
(i) A polynomial having one term is called a monomial. Since the degree of required monomial is 5, so the highest power of x in the monomial should be 5.
An example of a monomial of degree 5 is 2x5.
(ii) A polynomial having two terms is called a binomial. Since the degree of required binomial is 8, so the highest power of x in the binomial should be 8.
An example of a binomial of degree 8 is 2x8 − 3x.
(iii) A polynomial having three terms is called a trinomial. Since the degree of required trinomial is 4, so the highest power of x in the trinomial should be 4.
An example of a trinomial of degree 4 is 2x4 − 3x + 5.
(iv) A polynomial having one term is called a monomial. Since the degree of required monomial is 0, so the highest power of x in the monomial should be 0.
An example of a monomial of degree 0 is 5.
Q.6. Rewrite each of the following polynomials in standard form.
(i) x−2x2 + 8 + 5x3
(ii) 2/3 + 4y2 − 3y + 2y3
(iii) 6x3 + 2x − x5 − 3x2
(iv) 2 + t − 3t3 + t4 − t2
Ans.
A polynomial written either in ascending or descending powers of a variable is called the standard form of a polynomial.
(i) 8+x−2x2+5x3 is a polynomial in standard form as the powers of x are in ascending order.
(ii) 2/3 − 3y + 4y2+2y3 is a polynomial in standard form as the powers of y are in ascending order.
(iii) 2x−3x2 + 6x3 − x5 is a polynomial in standard form as the powers of x are in ascending order.
(iv) 2 + t − t2 − 3t3+ t4 is a polynomial in standard form as the powers of t are in ascending order.
|
44 videos|412 docs|54 tests
|
FAQs on RS Aggarwal Solutions: Polynomials- 1 - Mathematics (Maths) Class 9
| 1. What is a polynomial and how is it structured? |  |
| 2. How do you identify the degree of a polynomial? |  |
| 3. Can you explain the difference between a monomial, binomial, and trinomial? |  |
| 4. What are the common operations that can be performed on polynomials? |  |
| 5. How can we factor polynomials and why is it important? |  |

|
Explore Courses for Class 9 exam
|

|

















