Radiation | Electromagnetics - Electronics and Communication Engineering (ECE) PDF Download
In the following two lectures we will discuss the production of electromagnetic waves. Once produced they carry their energy and momentum and propagate in free space, may be to be received by an antenna. An antenna is a physical device which transmits or receives electromagnetic waves.
What causes a source to emit radiation? We have seen that charges at rest creates electrostatic field. A steady current, on the other hand is a source of magnetic field. Neither of these lead to radiation. However, it is known that accelerating charges emit radiation.
To discuss this in some detail, we fall back on our workhorse, viz., the Maxwell’s equations. Let us recall the potential formulation of the electromagnetic field that we had discussed earlier.
Using the expression for Faraday’s law,

We rewrite this in terms of vector potential 

This enablesus to express the quantity within the bracket as gradient of a scalar function V

Using Lorentz gauge condition

the Maxwell’s equations can be expressed as a pair of homogeneous wave equations,


Since the structure of both equations is same, we can solve either of them and write the solution to the remaining equation by similarity. We will solve the equation for the vector potential. The method of solution depends on defining a “Green’s function”.
Let us define a time Fourier transform through the equation

the inverse of which is

Substituting in Eqn. (2)

Taking inverse Fourier transform for both sides, we get

Defining  we get,
we get,

To obtain the solution of this equation, we define a subsidiary equation for a function known as the Green’s function

Thus the Green’s function satisfies a very similar equation in which the inhomogeneous term of the original equation has been replaced by a delta function. In terms of the Green’s function the formal solution of the equation for the vector potential can be written as a convolution,

To see how it comes about,

Remember that in the above, the primed coordinate  is for the source and the unprimed quantity refers to the point where the field is being evaluated. The solution must be spherically symmetric about the source point, i.e. depend on
is for the source and the unprimed quantity refers to the point where the field is being evaluated. The solution must be spherically symmetric about the source point, i.e. depend on  With this substitution, thee quation for the Green’s function becomes,
With this substitution, thee quation for the Green’s function becomes,

First consider R ≠ 0, for which the equation becomes

Expressing the Laplacian in spherical coordinates, as there is no dependence on angles,

the solution for which is seen to be

so that the Green’s function, excepting at the origin has the solution as a linear combination of an outgoing wave and an incoming wave.

What about the solution at the origin?
Let us take a small sphere of radius R0 around the origin. Since the argument of the delta function is included within the sphere, we have,

Since G(R) is singular only at the origin, we can calculate the integral over it within the sphere, by replacing it by the expression obtained for it except at the origin,

asR0 → 0
Thus,



Substituting this into the preceding integral, we get
A+B=1
Thus we have,

We will take the outgoing solution and proceed further.

Let us take the inverse Fourier transform of the above to get  It may, however, be remembered that
It may, however, be remembered that  has ω dependence,
has ω dependence,

Parallely, one can write, for the scalar potential

Note that the potential at time t at the position where it is being calculated is given in terms of current in the source at an “earlier time”  The potential is influenced by the wave which came from the source at a time which is earlier by the time taken by the electromagnetic wave to travel this distance. This is known as the “retarded” potential. The other solution is the incoming wave solution which would give to an “advanced” solution.
The potential is influenced by the wave which came from the source at a time which is earlier by the time taken by the electromagnetic wave to travel this distance. This is known as the “retarded” potential. The other solution is the incoming wave solution which would give to an “advanced” solution.
Example : Localized oscillation of charge or current
Let us consider a localized source of charge or current, given by


Thus we have,

and, similarly,

where k=ω/c
There are three regions of interest, assuming that the source is confined to a small region of space with typical dimension d. The distance at which the field is being measured is  and the wavelength of the radiation is λ.
and the wavelength of the radiation is λ.
- Near field for which d <<R<<λ
- Intermediate zone for which d <<R<<λ
- Radiation zone or Far field with d <<λ<<R
Our primary interest will be in the radiation zone, which we will discuss in detail in the next lecture. We will have very little to say about the intermediate zone and its analysis is very complicated.
Consider the near field for which d <<R<<λ In this region  as a result of which we can replace
as a result of which we can replace  The expression for the vector potential becomes
The expression for the vector potential becomes

which is the familiar expression for the vector potential in magnetostatics. The only difference from the magnetostatic case is the time variation of  which is simply to multiply the expressions obtained in the static case by
which is simply to multiply the expressions obtained in the static case by  Thus we can say that the situation is “quasi-static” and we can borrow all our results from magnetostatics to discuss this region.
Thus we can say that the situation is “quasi-static” and we can borrow all our results from magnetostatics to discuss this region.
Tutorial Assignment
- Consider a thought experiment in which a charge q appears abruptly at the origin at time t=t1 and disappears equally abruptly at time t=t2 Find the retarded potentials for the problem.Determine the corresponding fields.
- . A long straight wire lying along the z axis carries a current given by
 Determine the retarded potentials and the electric and the magnetic fields.
Determine the retarded potentials and the electric and the magnetic fields.
Solutions to Tutorial Assignments
1. Since the charge is static only retarded scalar potential is generated. For time  the information that a charge has appeared at the origin has not reached the position x. Thus the potential is zero for such time. Likewise, though the charge has disappeared at time t2 , this information would not reach the position x till a later time
the information that a charge has appeared at the origin has not reached the position x. Thus the potential is zero for such time. Likewise, though the charge has disappeared at time t2 , this information would not reach the position x till a later time  Thus the potential is
Thus the potential is  and zero at other times. The corresponding field is
and zero at other times. The corresponding field is  in the same time interval and is zero at other times.
in the same time interval and is zero at other times.
2. The wire being charge neutral, the scalar potential is zero. The vector potential, because of cylindrical symmetry depends only on the distance s of the point of observation P from the wire, and is given by


Consider an element dz at a distance z form the origin (see figure). Information about the current element would reach the point P at a time  later than the time the current was actually established. Thus the current, as seen by the point P is given by
later than the time the current was actually established. Thus the current, as seen by the point P is given by

where  Now let us look at the range of integration. For an element dz located at a distance z from the origin to influence the field at the point P, its distance from P should be less than ct. Thus,
Now let us look at the range of integration. For an element dz located at a distance z from the origin to influence the field at the point P, its distance from P should be less than ct. Thus,  Hence the potential is given by
Hence the potential is given by

(the factor of 2 in front is because only the upper half of the wire is considered in the integration). The integral is straightforward and gives,

The electric field is given by

and the magnetic field is given by

Self Assessment Questions
- An long straight wire lies along the z direction. At time t= 0, a constant current |0 is switched on. Calculate the vector potential and the electric and the magnetic fields.
- A conducting wire is bent into a loop of two semicircles, one of radius R1 and the other R2, (<R1)connected by straight segments. The loop carries a current |(t) = |0t, which is directed anticlockwise on the shorter semicircle and clockwise on the other one.. Calculate the vector potential at the centre of the loop. Calculate the electric field at the centre. Can you calculate the magnetic field from the expression of the vector potential?

Solutions to Self Assessment Questions
1.The problem is very similar to Problem 2 of the Tutorial. The vector potential is given by

2.

Since the current is switched on at t=0, the (retarded) vector potential at the centre O is given by

Since  the second integral vanishes. We are left with
the second integral vanishes. We are left with  Note that the integral is a line integral over the loop, which is directed differently at different points of the loop. Let us take the loop to be in the x-y plane with directions as shown in the figure. Recall that the direction of
Note that the integral is a line integral over the loop, which is directed differently at different points of the loop. Let us take the loop to be in the x-y plane with directions as shown in the figure. Recall that the direction of  is along the direction of the current. The contribution from the two straight sections give
is along the direction of the current. The contribution from the two straight sections give  the negative sign is due to the fact that the current in both the sections are directed along the negative x direction.
the negative sign is due to the fact that the current in both the sections are directed along the negative x direction.
We now have to perform the integration over the two semicircles. Consider the integration over the bigger semicircle. We can resolve  The denominator of the integral also has R1 so that the integral becomes independent of R1 (In a similar way, the integral of the smaller semicircle will be independent of R2). The y-component of the integral would vanish by symmetrically placed elements on either side of the y-axis, leaving us with
The denominator of the integral also has R1 so that the integral becomes independent of R1 (In a similar way, the integral of the smaller semicircle will be independent of R2). The y-component of the integral would vanish by symmetrically placed elements on either side of the y-axis, leaving us with  as the value of the integral. The integral over the smaller semicircle is done in a similar way but its direction would be opposite because of the direction of the current. Thus the contribution from the two semicircles would cancel and the vector potential at the centre would be given by
as the value of the integral. The integral over the smaller semicircle is done in a similar way but its direction would be opposite because of the direction of the current. Thus the contribution from the two semicircles would cancel and the vector potential at the centre would be given by  The electric field is trivial and is given by
The electric field is trivial and is given by

Since the vector potential has been calculated only at a single point, it is not possible to calculate its curl and hence the magnetic field cannot be determined by the above calculation.
Radiation Zone Approximation
We had seen that the expression for the vector potential for a localized current distribution is given by
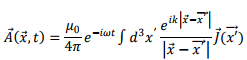
In near field approximation, this led to expression that was familiar to us in magnetostatics excepting for the time dependent multiplicative factor 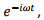 leading to our describing the situation as “quasi-stationary”. We will not have much to say about the intermediate zone as this case is very complicated. However, the far field approximation or the radiation zone for which the distance of the point of observation from the source is much greater than both the typical source dimension and the wavelength of radiation is of great interest to us and will be described in the following.
leading to our describing the situation as “quasi-stationary”. We will not have much to say about the intermediate zone as this case is very complicated. However, the far field approximation or the radiation zone for which the distance of the point of observation from the source is much greater than both the typical source dimension and the wavelength of radiation is of great interest to us and will be described in the following.
Let us write 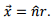 We expand
We expand 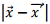 and
and 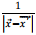 as follows:
as follows:
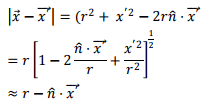
Thus
for situations where r<<x'.In a similar way, we have, keeping terms of the order of 1/r3 in Binomial expansion
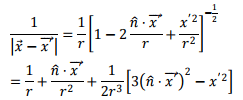
Using the above, we can write, retaining terms upto 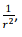
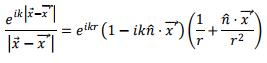
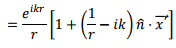
Electric Dipole Approximation
The lowest order approximation is to ignore the second term within bracket of the above. This gives
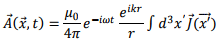
The integral above is rewritten by observing,
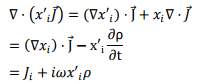
where we have used 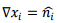 and the fact that the time dependence is given by
and the fact that the time dependence is given by 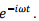 We replace each component of
We replace each component of 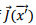 in the expression for vector potential by
in the expression for vector potential by 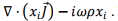 The integration over the first term is done by first converting it to a surface integral using the divergence theorem and letting the surface go toinfinity. Since the source dimension is confined to a limited region of space, this integral is zero and we are then left with,
The integration over the first term is done by first converting it to a surface integral using the divergence theorem and letting the surface go toinfinity. Since the source dimension is confined to a limited region of space, this integral is zero and we are then left with,
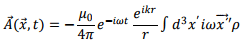
The integral 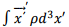 is the electric dipole moment of the source. Hence, we can write,
is the electric dipole moment of the source. Hence, we can write,
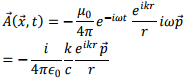
where we have used 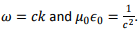
We can now obtain the expressions for the magnetic field and the electric field from the vector potential. Using the fact that 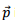 is a constant vector, we can write,
is a constant vector, we can write,
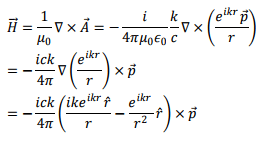
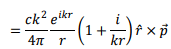
Thus the magnetic field direction is transverse to the direction of 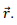 We will see, however, that the electric field has a longitudinal component as well.
We will see, however, that the electric field has a longitudinal component as well.
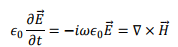
which gives
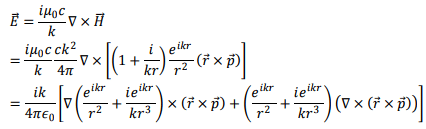
We have,
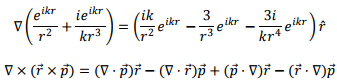
The first and the last terms of above are zero because 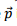 is a constant vector. We are left with
is a constant vector. We are left with

Substituting these, the electric field becomes
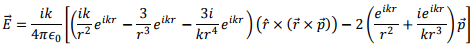
We reorganize the terms in the following fashion. Keep the first term within the first parenthesis in tact. For the second and the third terms, expand the vector triple product
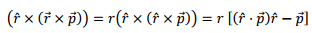
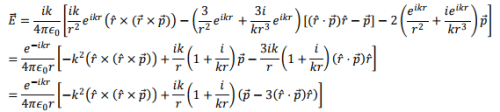
Note that, while the magnetic field was transverse, the electric field has a longitudinal component as well. Both these fields go as 1/r for large distances. However, for smaller distances, while the magnetic field vary as  the electric field goes as
the electric field goes as 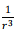 (the last term ).
(the last term ).
In the radiation zone, we are only interested in large distance behaviour. In this regime, the field expressions are,
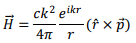
and the corresponding electric field is given by
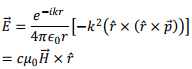
so that 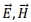 and
and 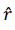 are mutually perpendicular.
are mutually perpendicular.
How does the emitted power, i.e., the average value of Poynting vector vary?
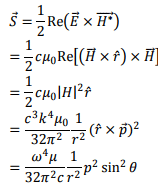
The amount of power flowing per unit solid anglein the direction of (θ, Ø) is given by
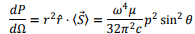
and the total radiated power is obtained by integrating over (θ, Ø). Since there is no azimuthal dependence, the integration over Ø gives 2π and we get,
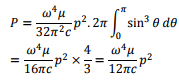
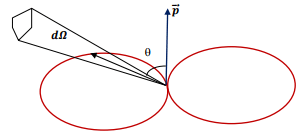
The following figure shows the “power pattern” in dipole approximation. It can be seen that the two lobes are symmetric about the dipole. The distance from the dipole to the lobe at any point gives the relative power in that direction with respect to the maximum. The total radiated power varies as the fourth power of the frequency.
Magnetic Dipole and Electric Quadrupole Approximation
We had started our discussion on radiation zone with the following expression for the vector potential,
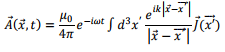
Retaining terms up to order 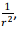 we had approximated
we had approximated
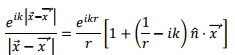
In the dipole approximation, we only retained the first term within the square bracket and ignored the remaining. Our next approximation is concerned with the second term. We will not write down the dipole term so that what we are discussing below is the correction to the dipole radiation. We consider
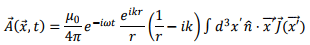
where we have taken out factors which are not concerned with the integration variable outside the integration.In order to perform the integration, let us write the dot product in an expanded form. Restricting only to the integration (the outside constants will be inserted later)
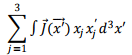
Using the argument given before, as the ettent of the source is limited, by extending the surface integral to infinite distances, we have, from the divergence theorem,
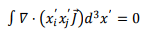
If we write this by expanding the divergence term, we have,
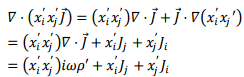
where, in the last step, we have used the equation of continuity. Inserting this into i-th component of the integral,
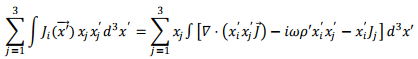
As mentioned before, the integral over the divergence is zero and we are left with
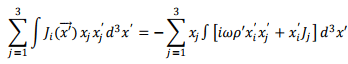
We replace the right hand side with half the term and add half of the left hand side to it
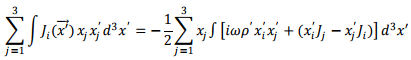
The term 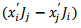 is easily seen to be component of a cross product and can be written as
is easily seen to be component of a cross product and can be written as
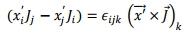
where 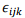 is the Levi-Civita symbol which is + 1 if i,j,k is an even permutation of 1,2 and 3, is −1 if it is an odd permutation and is zero if any pair of symols are equal. Using
is the Levi-Civita symbol which is + 1 if i,j,k is an even permutation of 1,2 and 3, is −1 if it is an odd permutation and is zero if any pair of symols are equal. Using
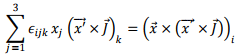
We also have,
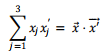
Thus
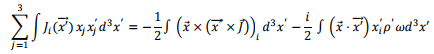
Adding three components
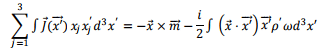
where the magnetic moment vector 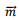 is given by
is given by

The term 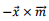 is the magnetic dipole term and the remaining term is the electrical quadrupole term. Substituting these in the expression for the vector potential for the magnetic dipole term becomes,
is the magnetic dipole term and the remaining term is the electrical quadrupole term. Substituting these in the expression for the vector potential for the magnetic dipole term becomes,
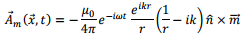
The magnetic field is now readily calculated. Suppressing the time variation,
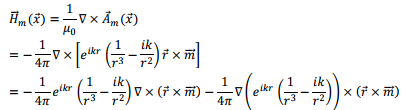
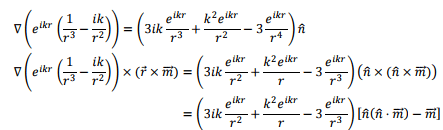
and

Combining these,
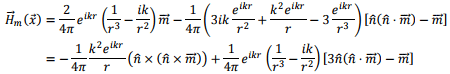
where we have restored the structure 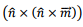 for the central term of the second expression retaining the expanded form for the remaining.
for the central term of the second expression retaining the expanded form for the remaining.
In the radiation zone, the first term, which varies as 1/r at large distances dominate and we have,
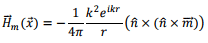
The corresponding electric field can be determined from Faraday’s law,
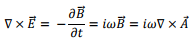
so that
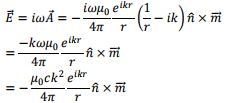
where we have retained only the leading term in radiation zone approximation.
The power radiated can be calculated in the same manner as we did for the electric dipole case,
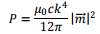
[The above formulae were for two specific cases of radiating systems, viz. oscillating electric dipole and oscillating magnetic dipole. The power radiated from an arbitrary current and charge distribution is given by the formula
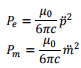
where the double dots indicate double differentiation with time. For the specific cases mentioned above, these boil down to respective formulae on taking the time average.
Tutorial Assignment
- A spherically symmetric charge distribution oscillates in a radial direction such that it remains spherically symmetric at all time. Show that no radiation is emitted.
- An electric dipole of strength 10−7 C-m oscillates at an angular frequency of 3 × 108 rad/s. The dipole is placed along the z-axis. (a) Find the strength of the electric field measured by an observer located at (5,0,0) km. (b) What is the phase difference between the oscillation frequency of the dipole and that seen by this observer? (c) What is the average power measured at this location? (d) What would be the average power measured if the observer was located at (0,0,5) km instead of the position defined in (a)? (e) What is the total rate at which the dipole radiates power?
- A wire of length 1 m is bent in a circular loop to form a magnetic dipole antenna. The current in the dipole varies as |= |0 sin ωt with ω = 3 × 108 rad/s and |0 = 2 A. Determine the electric and the magnetic field as seen by an observer at a large distance r from the dipole at an angle θto the axis of the loop. Calculate the total power radiated.
Solutions toTutorial Assignment
1. Spherical symmetry implies that both the electric and the magnetic field remains radial at all times. Using Gauss’s law, this implies 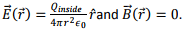 This implies the Poyntingvector
This implies the Poyntingvector  hence there is no radiation.
hence there is no radiation.
2. Since the distance from the source is large, it is reasonable to assume that the observer is in the radiation zone. In this region we use 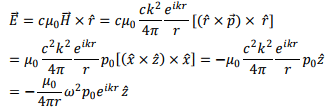
where we have used the fact that the observer is located along the x-axis .
(a) The field is thus directed opposite to the direction of the dipole moment vector, consi8stent with the fact that the dipole moment vector is along the direction from the negative to the positive charge. The strength of the electric field obtained by substituting given values is 0.18 V/m.
(b) As discussed in the last lecture, the wave generated at time t arrives at 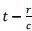 at the observer’s location. Thus the phase difference between the wave at the source and that at the location of
at the observer’s location. Thus the phase difference between the wave at the source and that at the location of 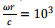 radians.
radians.
(c) Since the observer is in the equatorial plane θ= 90∘ . The power measured at this location is  Watts.
Watts.
(d) Along the axis of dipole θ= 0∘ so that no power is radiated in this direction.
(e) The total power radiated is given by 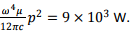
3. Take the dipole along the x-y plane with its axis being along the z-axis. Consider the position vector of the of observer to be in the x-z plane,
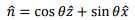
The magnetic moment vector is given by 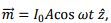 where A is the area of the loop. The complex magnetic field is given by
where A is the area of the loop. The complex magnetic field is given by
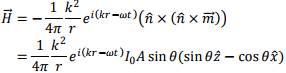
The electric field is given by
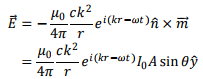
The average Poynting vector is given by
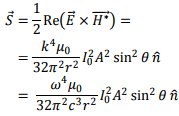
The power flowing out per unit solid angle is given by
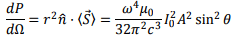
The total power radiated is obtained by integrating over the solid angle and is given by
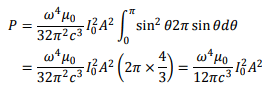
The area of the loop is obtained from its circumference of 1m to be 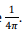 Substituting
Substituting 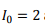 and other constants, we get the total power radiated to be 0.253 W.
and other constants, we get the total power radiated to be 0.253 W.
Self Assessment Questions
1. Two point charges, q each, are attached to the ends of a rigid rod of length ℓ. The rod is rotated with an angular speed ω about an axis through the centre of the rod and perpendicular to it. Calculate the electric and the magnetic dipole moment of the system taking the centre of the rod as the origin. What is the total power radiated by this system?
2. An electric dipole of strength ρ0 initially lies along the x-axis centred at origin. The dipole rotates in the x-y plane about the z-axis at an angular frequency ω. Calculate the radiation field and the radiated power as seen by an observer in the x-z plane at an angle θ to the z-axis.
3. Neutron stars are a class of very dense stars consisting primarily of neutrons. The neutron star rotates with an angular frequency ω about an axis which makes an angle α with the direction of the magnetic moment. Assume the radius of the star to be 10 km and the angular frequency of rotation to be 100 rad/s about the z-axis which makes angle of α= 45∘ with the magnetic moment vector of the neutron star. Take the strength of the magnetic field at the magnetic equator to be 108T. Calculate the total power radiated.
Solutions to Self Assessment Questions
1. The electric dipole moment about the centre is zero as the position vector of the two (equal) charges are always directed oppositely. Magnetic dipole moment can be calculated by observing that charge 2q is rotating with a time period 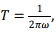 which is equivalent to a current 4 πqω. The area of the current loop is
which is equivalent to a current 4 πqω. The area of the current loop is 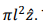 Thus the magnetic moment is given by
Thus the magnetic moment is given by 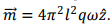 Both the electric and the magnetic dipoles are constant in time and hence there is no radiation emitted by the system.
Both the electric and the magnetic dipoles are constant in time and hence there is no radiation emitted by the system.
2. The dipole vector can be written as
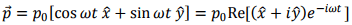
Since the observer is in x-z plane, y-direction is perpendicular to the direction of observation 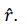
We can write 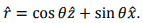 Note that
Note that
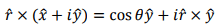
Using these, we can write the complex magnetic field as
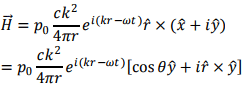
The corresponding electric field is given by
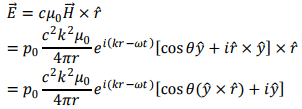
The average Poynting vector is given by
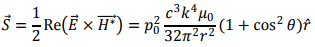
The power flowing out per unit solid angle is given by
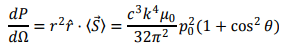
The total power radiated is given by integrating the above over the solid angle. Since there is no azimuthal dependence, we have,
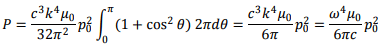
3. The magnetic field of a dipole at 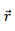 is given by the expression
is given by the expression
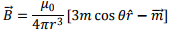
where θ is the angle between 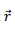 and
and 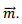 At the equator, θ= 90∘ so that the strength of the magnetic field is
At the equator, θ= 90∘ so that the strength of the magnetic field is
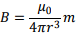
Substituting the given values, the magnitude of the magnetic field is 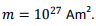
As the star rotates about an axis which does not coincide with the magnetic moment vector, the direction of the magnetic moment vector precesses about the z-axis. This accounts for the radiation. It was pointed out that the magnetic dipole radiation power is proportional to the square of the second derivative of the magnetic moment. We can write
The magnetic moment vector as 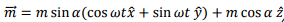
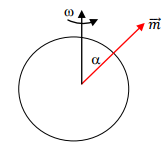
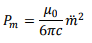
Substituting numerical values, one gets the power radiated to be 1.2 × 1029 W.
|
11 videos|64 docs|89 tests
|
FAQs on Radiation - Electromagnetics - Electronics and Communication Engineering (ECE)
| 1. What is radiation? |  |
| 2. How does radiation affect the human body? |  |
| 3. What are the different types of radiation? |  |
| 4. How can we protect ourselves from radiation exposure? |  |
| 5. What are the sources of radiation in our daily lives? |  |


















