Half Life Time, Mean Life & Radioactivity Series | Inorganic Chemistry PDF Download
16. Half-life (T1/2):
(a) The time in which the number of atoms (N) reduces to half of its initial value (N0) is defined as the halflife of the element (i.e. half of the atoms decay). 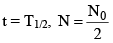
(b) The time in which the activity reduces to half of its initial value is defined as half life.
At t = T1/2, 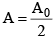
(c) Its unit is second
(d) Formulae of half life
(i) 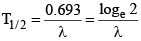
(ii) 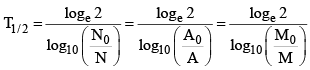
(iii) T1/2 = 1/n where n = No. of half life
(iv) Time of disintegration 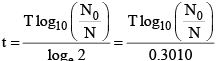
17. Mean life (t):
(a) The time, for which a radioactive material remains active, is defined as mean life of that material:
(b) 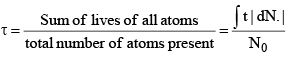
(c) The average time taken in decaying by the atoms of an element is defined as its mean life t.
(d) τ = 1/λ
(e) Its units are second, minute, hour day, month, year etc.
(f) Mean life does not depend on the mass of material. It depends on the nature of the material.
(g) The magnitude of slope of decay curve is equal to the mean life.
(h) Relation between the mean life and half -life.
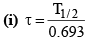
(ii) τ = 1.44 T1/2
(iii) τ > T1/2
(iv) The time, in which the number of radioactive atoms decays to 1/e or 37% of its initial value, is defined as the mean life of that material.
18. Important Formulae Related to Law of Disintegration (τ):
(a) N = N0e–λt
(b) A = A0e–λt
(c) M = M0e-λt
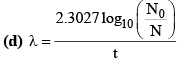
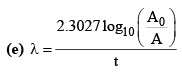
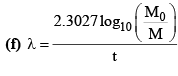
(g) λ = λα + λβ
(h) 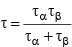 (where two particles decay simultaneously)
(where two particles decay simultaneously)
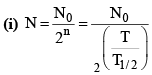
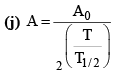
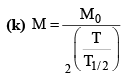
19. Useful Hints:
(i) Percentage decreases in activity 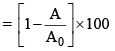
(ii) Number of atoms remaining after n half lives 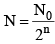
(iii) Number of atoms decayed after time 
(iv) The fraction of radioactive material at time 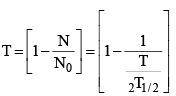
(v) Percentage of radioactive material decayed at time 
(vi) Percentage of radioactive material decayed in n half lives 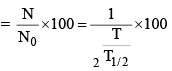
(vii) Fraction of radioactive material decayed in n half lives 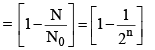
(viii) Percentage of radioactive material decayed in n half lives 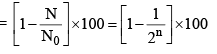
(ix) Percentage of radioactive material remaining after n half-lives. 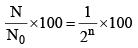
(x) When decay process is too slow then N = N0 – N0λt or N = - (N0λ)t + N0
(xi) N-t graph is a straight line with -ve slope, for slow decay process.
20. Characteristics of α, β and γ rays
S. No. | Property | α-Particles | β-Particles | γ-rays |
1. | Natural and value of charge | Positive and double of the charge of the proton | Negative and equal to the charge of electron 1.6 × 10-19 C | Uncharged (Nautral) |
2. | Nature of particle | Doubly ionized helium atom (2 protons and 2 neutrons) | Electron (or) position | Electromagnetic waves |
3. | Mass | Four times the mass of the proton (4 × 1.67 x 10-27 kg) | Equal to the mass of electron 9.1 x 10-31 kg | Mass less |
| 4. | Specific charge q/m | 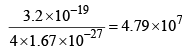 | 1.7 × 1011 Ckg–1 | Uncharged and mass less |
5. | Explained by | Tunnel effect | Neutrino hypothesis | Transitions of nuclei into the ground energy level after a and P-decay |
6. | Effect of electric and magnetic fields | Deflected by electric and magnetic fields | Deflected by electric and magnetic fields | Unaffected |
7. | Penetrating power | 1 | 100 | 10000 |
8. | Ionizing power | 100000 | 100 | 1 |
9. | Velocity | Less than the velocity of light (1.4 × 104 m/s to 2.2 x 107 ms-1 | Approximately equal to the velocity of light | 3 × 108 m/s |
10. | Mutual interaction with matter | Produce heat | Produce heat | Produce the phenomenon of Photoelectric effect, Compton |
21. α-emission
(a) Characterstictics of α-decay:
(i) The spectrum of α-particles is a discrete line spectrum.
(ii) Spectrum of α-particles has fine structure i.e. every spectral line consists of a number of fine lines.
(iii) The α-emitt ing nuclei have discrete energy levels i.e energy levels in nuclei are analogous to discrete energy levels in atoms.
(iv) α-decay is explained on the basis of tunnel effect.
(v) Geiger-Muller law 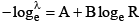 for radioactive series B is same whereas A is different.
for radioactive series B is same whereas A is different.
(b) Range of α-particles:
(i) The maximum distance traversed by α-particles in air before being finally stopped is defined as the range of α-particles.
(ii) The maximum distance traversed by α-part icles before being finally absorbed after io nizing gas molecules, is defined as the range of α-particles.
(iii) The range of α-part icles in air is fro m 2.6 cm to 8.6 cm.
(iv) Relations between the range of α-particles and their energy
(I) R = 0.318 E3/2
(II) log R = log 0.318 + 3/2 log E
(c) Size of the nucleus decreases by α-emission
22. Characteristics of β-decay:
(i) The energy spectrum of β-particles is continuous i.e. β-particles of all energies upto a certain maximum are emitted.
(ii) The number of such β-particles is maximum whose energy is equal to the maximum probable energy i.e. at E = Emp, NB = maximum
(iii) There is a characteristic maximum value of energy in the spectrum of β-particles which is known as the end point energy (E0)
(iv) In β-decay process, a neutron is converted into proton or proton is converted into neutron.
0n1 = 1p1 + –1e0 (β– Particle)
1p1 = 0n1 + 1e0 (β+ Particle)
(v) The energy of β-particles emitted by the same radioactive material may be same or different.
(vi) The energy of β-particles with energy E = E0 (end point energy) is zero.
23. Neutrino Hypothesis:
(a) According to Pauli, whenever neutron is converted into proton or proton into neutron then this process is accompanied with the emission of a new particle to which he named as neutrino.
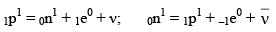
(b) Properties of neutron:
(i) The charge on neutrino is zero
(ii) The rest mass of neutrino is zero
(iii) Its spin angular momentum is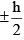
(iv) Its speed is equal to that of light
(v) It has finite magnetic moment but the magnitude is very small
(vi) It antiparticle is ant i-neutrino.
(vii) The linear momentum vector 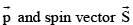 are mutually in opposite directions.
are mutually in opposite directions.
(viii) Its energy is equal to (Eend – Eβ)
(ix) It does not interact with matter.
(x) Neutrino was discovered by Pauli and its experimental verificat ion is done by Reines and Cowan.
24. Characterstics of γ-decay
(i) The spectrum of γ-rays is a discrete line spectrum
(ii) Whenever, α or β-particles is emitted by a nucleus then the daughter nucleus is left in the excited state. It suddenly makes transition in the ground state thereby emitting γ-rays. (iii) Knowledge about nuclear energy levels is obtained by γ-spectrum.
(iv) γ-rays interact with matter as a consequence of which the pheno mena of photoelectric effect, Compton effect and pair production happen. (At low energy photoelectric effect and at high energy pair-production are effective).
25. Intensity of γ-rays in materials
(i) When γ-rays penetrate matter, then their intensity (a) decreases exponentially with depth (x) inside the matter. The intensity of γ-rays at depth x inside the matter is given by I = I0e–μx
(ii) The thickness of matter, at which the intensity of γ-rays (I) reduces to half its initial maximum value (I0), is known as its half-life value thickness. 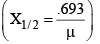
(iii) The reciprocal of the distance inside matter, at which the intensity (I) reduces to 1/e
or 37% of its maximum value (I0), is defined as the coefficient of absorption (μ) of that material.
(iv) Coefficient of absorption

(II) μ depends on the wavelength of γ-rays (μ α λ3) and the nature of absorbind material.
26. Radioactive Series:
If parent element is unstable then it will dissociate into daughter element & if this daughter element is still unstable, then it will again dissociate into a new daughter element & process continuous till the format ion of a stable element. Series of element obtained fro m parent element to the finally stable non-radioactive element is known as radioactive disintegration series.
(4n +1) is artificial series & (4n + 2), (4n +3) are natural series.
S. No. | Series | Name of the series | Initial element | Final element | Nature of series | No of α & β Particles emitted |
1. | 4n + 2 | Uranium series | 92U238 | 82Pb206 | Natural | 8α, 6β |
2. | 4n + 3 | Actinium series | 92U235 | 82Pb207 | Natural | 7α, 4β |
3. | 4n | Thorium series | 90Th232 | 82Pb208 | Natural | 6α, 4β |
4. | 4n + 1 | Neptunium series | 93U237 | 83Bi209 | Artificial | 7α, 4β |
27. To Calculate no of α-particles and β-Particles emitted
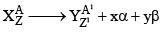
x: no of α-particles emitted y: no of β-particles emitted
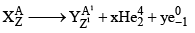
A = A1 + 4x
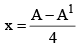
Z = Z1 + 2x – y
y = Z1 – Z + 2x
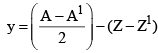
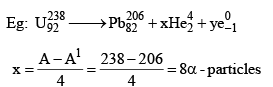
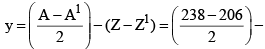 (92 - 82) = 16 - 10 = 6β - particles
(92 - 82) = 16 - 10 = 6β - particles
28. Units of radioactivity:
The unit of radioactivity is curie (Ci). It is the quantity of any radioactivity substance which has decay rate of 3.7 × 1010 disintegrat ions per second.
1 millicurie (mCi) = 3.7 × 107 disintegrat ions per sec.
1 microcurie (μCi) = 3.7 × 104 disintegrat ions per sec.
There is another unit called Rutherford (Rd) which is defined as the amount of a radioactive substance which undergoes 106 disintegrat ions per second.
1 milli Rutherford = 103 disintegrat ion per sec.
1 micro Rutherford = 1 disintegration per sec.
The SI unit radioactivity is proposed as Becquerel which refers to one dps.
1 curie = 3.7 × 104 Rutherford.
1 curie = 3.7 GBq
Here, G stands for 109, i.e., giga.
29. Isotopes, Isobars and Isotones:
S. No. | Isotopes | Isobars | Isotones |
1. | The atoms of the same elements whose charge number (Z) is same but mass number is different are known as isotopes. | The atoms with mass number same and charge number different are known as isobars. | The atoms with same neutron number but A and Z are different are known as isotones |
2. | Chemical properties are same | Chemical properties are different | Chemical properties are different |
3. | Number of electrons is same | Number of electrons is different | Number of properties are different |
4. | Occupy same place in periodic table | Occupy different places in periodic table | Occupy different places in periodic table. |
5. | Example: 8O16, 8O17, 8O18, 1H1, 1H2, 1H3, 10Ne20, 10Ne20, 1oNe21, 1oNe22 | 1H3 and 2He3 6C14 and 7N14 | 3Li7 and 4Be8 1H2 and 2He3 1H3 and 2He4 |
30. Radioactive Isotopes:
The isotopes of elements which spontaneously decay by emitting radioactive radiations are defined as radioactive isotopes.
They are two types.
(a) Natural radioactive isotopes
(b) Artificial radioact ive isotopes
(a) Natural radioactive isotopes: Those radioact ive isotopes which exist naturally are known as natural radioactive isotopes. e.g.Th232, Pu240 etc.
(b) Artificial radioactive isotopes: Those isotopes, which are prepared artificially by bo mbarding fundamental particles like α, β, γ, p, n etc, no matter, are known as artificial isotopes.
|
48 videos|92 docs|41 tests
|
FAQs on Half Life Time, Mean Life & Radioactivity Series - Inorganic Chemistry
| 1. What is half-life time and how is it calculated? |  |
| 2. What is the mean life of a radioactive substance? |  |
| 3. What is a radioactivity series? |  |
| 4. How do half-life time and mean life relate to each other? |  |
| 5. Can the half-life time or mean life of a radioactive substance be altered? |  |

|
Explore Courses for Chemistry exam
|

|


















