Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Range & Quartiles
Range & Quartiles | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Range & IQR
What are the range and interquartile range (IQR)?
- The three measures of central tendency—mean, median, and mode—indicate what is typical within the data, showing what is approximately in the center.
- The range and interquartile range (IQR) quantify the dispersion of the data.
- These metrics are applicable exclusively to numerical data.
- Fortunately, both are straightforward to calculate.
How do I work out the range?
- The range is calculated as the difference between the highest and lowest data values.
- It indicates the extent of data dispersion.
- You can recall this as "Hi - Lo."
- There is a potential issue with using the range:
- Since it takes into account only the highest and lowest values, it can be affected by outliers.
- These outliers may not accurately reflect the overall spread of the data.
How do I find the quartiles?
- The median divides the data set into two equal parts, positioned halfway along the data.
- Quartiles, as their name implies, split the data set into four equal parts:
- The lower quartile (LQ) is located one quarter of the way through the data (when ordered).
- The upper quartile (UQ) is located three quarters of the way through the data.
- The median can also be referred to as the second quartile.
- To find quartiles, first use the median to split the data set into lower and upper halves:
- Ensure the data is sorted numerically.
- If the data set has an even number of values:
- The first half consists of the lower values, and the second half consists of the higher values.
- In this case, all data points are included in one of the two halves.
- If the data set has an odd number of values:
- The lower half includes all values below the median.
- The upper half includes all values above the median.
- The median itself is excluded from both halves.
- The lower quartile is the median of the lower half of the data set, and the upper quartile is the median of the upper half.
- Find the quartiles in the same way you would find the median for any data set, focusing only on the lower or upper half accordingly.
- Sometimes you may also see the quartiles given in formula form
- For n data values:
- the lower quartile is the
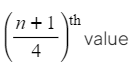
- the upper quartile is the
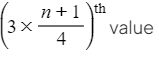
- the lower quartile is the
- Using these can save finding the median and splitting the data into two halves
- For n data values:
How do I work out the interquartile range (IQR)?
- The interquartile range (IQR) is the difference between the upper quartile (UQ) and the lower quartile (LQ).
- To calculate the IQR, you must first determine the quartiles.
- The formula for the interquartile range is IQR = UQ - LQ.
- The IQR measures the spread of the middle 50% of the data, making it resistant to the influence of extreme values.
- Conversely, the range of a data set can be impacted by extremely high or low values.
Question for Range & QuartilesTry yourself: What is the range?View Solution
The document Range & Quartiles | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
42 videos|395 docs|19 tests
|
FAQs on Range & Quartiles - Mathematics for GCSE/IGCSE - Class 10
| 1. What is the purpose of calculating the range and quartiles in statistical analysis? |  |
Ans. The range and quartiles help in understanding the spread and distribution of data, allowing for better analysis and comparison of different data sets.
| 2. How can quartiles help in identifying outliers in a data set? |  |
Ans. Quartiles divide a data set into four equal parts, making it easier to identify extreme values that may be outliers when compared to the rest of the data.
| 3. How does the interquartile range (IQR) differ from the range in statistical analysis? |  |
Ans. The range is the difference between the maximum and minimum values in a data set, while the IQR is the range of the middle 50% of the data, providing a more focused measure of data variability.
| 4. Why is it important to calculate quartiles in data analysis? |  |
Ans. Quartiles provide insights into the distribution and variability of data, helping in making informed decisions and drawing meaningful conclusions from statistical analysis.
| 5. How can understanding statistical ranges and quartiles help in making predictions based on data trends? |  |
Ans. By analyzing quartiles and ranges, one can identify patterns, trends, and outliers in data, which can be used to make accurate predictions and forecasts based on statistical analysis.
Related Searches















