Ratio and Proportion | Math Olympiad for Class 5 PDF Download
What is Ratio and Proportion?
- Ratio and proportion are fundamental concepts in mathematics with practical applications in real life scenarios.
- Ratios represent the quantitative relationship between two quantities and are often expressed as a comparison of two numbers.
- Examples of ratios in real life include speed (distance/time) and price (currency/unit).
- Proportion is an equation that states two ratios are equal to each other.
- In the context of proportions, if one ratio is given (such as the time taken by a train to cover 100km/hr), the corresponding equivalent ratio can be found (such as the time taken to cover 500km in 5 hours).
- Proportions provide a way to express the relationship between different quantities in a consistent manner.
Ratio Meaning
In certain situations, the comparison of two quantities by the method of division is very efficient. We can say that the comparison or simplified form of two quantities of the same kind is referred to as a ratio. This relation gives us how many times one quantity is equal to the other quantity. In simple words, the ratio is the number that can be used to express one quantity as a fraction of the other ones.
The two numbers in a ratio can only be compared when they have the same unit. We make use of ratios to compare two things. The sign used to denote a ratio is ‘:’.
A ratio can be written as a fraction, say 2/5. We happen to see various comparisons or say ratios in our daily life.
Hence, the ratio can be represented in three different forms, such as:
- a to b
- a : b
- a/b
Key Points to Remember:
- The ratio should exist between the quantities of the same kind
- While comparing two things, the units should be similar
- There should be significant order of terms
- The comparison of two ratios can be performed, if the ratios are equivalent like the fractions
Definition of Proportion
Proportion is an equation that defines that the two given ratios are equivalent to each other. In other words, the proportion states the equality of the two fractions or the ratios. In proportion, if two sets of given numbers are increasing or decreasing in the same ratio, then the ratios are said to be directly proportional to each other.
For example, the time taken by train to cover 100km per hour is equal to the time taken by it to cover the distance of 500km for 5 hours. Such as 100km/hr = 500km/5hrs.
Ratio and proportions are said to be faces of the same coin. When two ratios are equal in value, then they are said to be in proportion. In simple words, it compares two ratios. Proportions are denoted by the symbol ‘::’ or ‘=’.
The proportion can be classified into the following categories, such as:
- Direct Proportion
- Inverse Proportion
- Continued Proportion
Now, let us discuss all these methods in brief:
Direct Proportion
The direct proportion describes the relationship between two quantities, in which the increases in one quantity, there is an increase in the other quantity also. Similarly, if one quantity decreases, the other quantity also decreases. Hence, if “a” and “b” are two quantities, then the direction proportion is written as a∝b.
Inverse Proportion
Continued Proportion
Consider two ratios to be a: b and c: d.
Then in order to find the continued proportion for the two given ratio terms, we convert the means to a single term/number. This would, in general, be the LCM of means.
For the given ratio, the LCM of b & c will be bc.
Thus, multiplying the first ratio by c and the second ratio by b, we have
First ratio- ca:bc
Second ratio- bc: bd
Thus, the continued proportion can be written in the form of ca: bc: bd
Ratio and Proportion Formula
Now, let us learn the Maths ratio and proportion formulas here.
Ratio Formula
Assume that, we have two quantities (or two numbers or two entities) and we have to find the ratio of these two, then the formula for ratio is defined as;
a: b ⇒ a/b
where a and b could be any two quantities.
Here, “a” is called the first term or antecedent, and “b” is called the second term or consequent.
Example: In ratio 4:9, is represented by 4/9, where 4 is antecedent and 9 is consequent.
If we multiply and divide each term of ratio by the same number (non-zero), it doesn’t affect the ratio.
Example: 4:9 = 8:18 = 12:27
Proportion Formula
Now, let us assume that, in proportion, the two ratios are a:b & c:d. The two terms ‘b’ and ‘c’ are called ‘means or mean term,’ whereas the terms ‘a’ and ‘d’ are known as ‘extremes or extreme terms.’
a/b = c/d or a : b :: c : d
Example: Let us consider one more example of a number of students in a classroom. Our first ratio of the number of girls to boys is 3:5 and that of the other is 4:8, then the proportion can be written as:
3 : 5 :: 4 : 8 or 3/5 = 4/8
Here, 3 & 8 are the extremes, while 5 & 4 are the means.
Note: The ratio value does not affect when the same non-zero number is multiplied or divided on each term.
Important Properties of Proportion
The following are the important properties of proportion:
- Addendo – If a : b = c : d, then a + c : b + d
- Subtrahendo – If a : b = c : d, then a – c : b – d
- Dividendo – If a : b = c : d, then a – b : b = c – d : d
- Componendo – If a : b = c : d, then a + b : b = c+d : d
- Alternendo – If a : b = c : d, then a : c = b: d
- Invertendo – If a : b = c : d, then b : a = d : c
- Componendo and dividendo – If a : b = c : d, then a + b : a – b = c + d : c – d
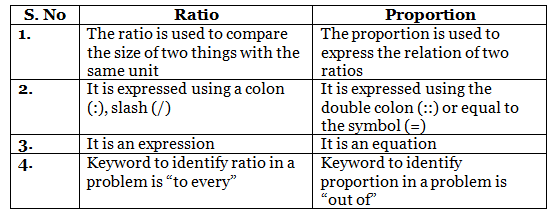
Difference Between Ratio and Proportion
To understand the concept of ratio and proportion, go through the difference between ratio and proportion given here.
Fourth, Third and Mean Proportional
If a : b = c : d, then:
- d is called the fourth proportional to a, b, c.
- c is called the third proportion to a and b.
- Mean proportional between a and b is √(ab).
Comparison of Ratios
If (a:b)>(c:d) = (a/b>c/d)
The compounded ratio of the ratios: (a : b), (c : d), (e : f) is (ace : bdf).
Duplicate Ratios
If a:b is a ratio, then:
- a2:b2 is a duplicate ratio
- √a:√b is the sub-duplicate ratio
- a3:b3 is a triplicate ratio
Ratio and Proportion Tricks
Let us learn here some rules and tricks to solve problems based on ratio and proportion topics.
- If u/v = x/y, then uy = vx
- If u/v = x/y, then u/x = v/y
- If u/v = x/y, then v/u = y/x
- If u/v = x/y, then (u+v)/v = (x+y)/y
- If u/v = x/y, then (u-v)/v = (x-y)/y
- If u/v = x/y, then (u+v)/ (u-v) = (x+y)/(x-y), which is known as componendo -Dividendo Rule
- If a/(b+c) = b/(c+a) = c/(a+b) and a+b+ c ≠0, then a =b = c
Ratio and Proportion Summary
- Ratio defines the relationship between the quantities of two or more objects. It is used to compare the quantities of the same kind.
- If two or more ratios are equal, then it is said to be in proportion.
- The proportion can be represented in two different ways. Either it can be represented using an equal sign or by using a colon symbol.(i.e) a:b = c:d or a:b :: c:d
- If we multiply or divide each term of the ratio by the same number, it does not affect the ratio.
- For any three quantities, the quantities are said to be in continued proportion, if the ratio between the first and second quantity is equal to the ratio between the second and third quantity.
- For any four quantities, they are said to be in continued proportion, if the ratio between the first and second quantities is equal to the ratio between the third and fourth quantities
Ratio And Proportion Examples
Example 1: Are the ratios 4:5 and 8:10 said to be in Proportion?
Solution: 4:5= 4/5 = 0.8 and 8: 10= 8/10= 0.8
Since both the ratios are equal, they are said to be in proportion.
Example 2: Are the two ratios 8:10 and 7:10 in proportion?
Solution: 8:10= 8/10= 0.8 and 7:10= 7/10= 0.7
Since both the ratios are not equal, they are not in proportion.
Example 3: The earnings of Rohan is 12000 rupees every month and Anish is 191520 per year. If the monthly expenses of every person are around 9960 rupees. Find the ratio of the savings.
Solution: Savings of Rohan per month = Rs (12000-9960) = Rs. 2040
Yearly income of Anish = Rs. 191520
Hence, the monthly income of Anish = Rs. 191520/12 = Rs. 15960.
So, the savings of Anish per month = Rs (15960 – 9960) = Rs. 6000
Thus, the ratio of savings of Rohan and Anish is Rs. 2040: Rs.6000 = 17: 50.
Example 4: Twenty tons of iron is Rs. 600000 (six lakhs). What is the cost of 560 kilograms of iron?
Solution: 1 ton = 1000 kg
20 tons = 20000 kg
The cost of 20000 kg iron = Rs. 600000
The cost of 1 kg iron = Rs{600000}/ {20000}
= Rs. 30
The cost of 560 kg iron = Rs 30 × 560 = Rs 16800
Example 5: The dimensions of the rectangular field are given. The length and breadth of the rectangular field are 50 meters and 15 meters. What is the ratio of the length and breadth of the field?
Solution: Length of the rectangular field = 50 m
Breadth of the rectangular field = 15 m
Hence, the ratio of length to breadth = 50: 15
⇒ 50: 15 = 10: 3.
Thus, the ratio of length and breadth of the rectangular field is 10:3.
|
32 videos|57 docs|45 tests
|

|
Explore Courses for Class 5 exam
|

|

















