Ratio to Percent | Mathematics for JAMB PDF Download
In math, the ratio to percent conversion is very useful to make comparisons of each part with the whole. A ratio compares any two parts of a whole. For example, the ratio of sugar and salt in a solution is 3:1. It is telling us that in the solution, sugar is three times that of salt. Percentages are a very specific type of ratio. A percent compares any one part of the whole against the whole, instead of making comparisons with the individual parts with each other. In the same example, the percentage of sugar in the solution is 75% and the percentage of salt is 25%. But how did we convert 3:1 into percentages?
Ratio to Percent Formula
There is a formula to convert the ratio to a percent. It can be applied directly with any values to get the required percentage. The ratio to percent formula is given below:
Percentage = Ratio × 100
It is expressed with a percentage symbol (%).
How to Convert Ratio to Percent?
Before learning about the conversion of ratio to percent, let us briefly discuss the meaning of ratios and percents first. A ratio is a relation or a comparison between two quantities of the same kind and of the same unit. There are three ways to express ratios, which are part to part ratios, part to whole ratios, and whole to part ratios. Part to part ratios compares the quantity of two parts with each other. An example of this relationship is given at the beginning of this article (the ratio of sugar and salt in a solution is 3:1). Another example could be the ratio of the number of boys and girls in the class - 2:3. Taking the same example, if we represent the ratio of the number of boys and the total number of students, the ratio would be 2:5 (as whole = total number of parts = 2 + 3= 5). This is an example of a part to whole ratio. The same ratio, if represented as 5:2, is an example of a whole-to-part relationship.
To convert the ratio to percent form, we need to first identify the ratio. And then we can apply that ratio in the above 'ratio to percent formula' to get the value of percentage. For example, if it is given that the ratio of apples to oranges in a basket is 5:8 and we have to find the percentage of apples in the basket, then we need to first find the ratio of apples to fruits in the basket. The total number of fruits in the basket is 5 + 8, which is 13 fruits. So, the ratio of apples to fruits is 5:13. Now, we can find the percentage as,
Percentage = [Ratio × 100] %
Percentage = 5/13 × 100
Percentage = 38.46%
In the same way, the ratio of oranges to fruits is 8:13. The percent of oranges in the basket is [8/13 × 100] % = 61.54%. Look at one more example of converting 1:4 to percent in the image below.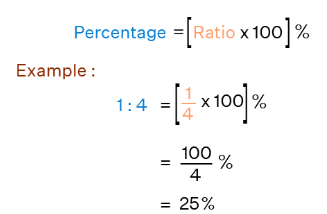
To conclude, the steps to convert a ratio to a percent are given below:
- Step 1: Identify the ratio.
- Step 2: Express the ratio a:b in the form of a fraction a/b.
- Step 3: Multiply the fraction by 100.
- Step 4: Simplify and write the answer with the percent symbol (%).
Ratio to Percentage Table
The ratio to percent table is a quick way to provide the percentage values of some commonly used ratios. Look at the ratio to percentage table given below.
|
139 videos|82 docs|101 tests
|


















