Rational Numbers | Mathematics for ACT PDF Download

Introduction

Rational numbers are in the form of p/q, where p and q can be any integer and q ≠ 0. This means that rational numbers include natural numbers, whole numbers, integers, fractions of integers, and decimals (terminating decimals and recurring decimals).

What are Rational Numbers?

The word 'rational' originated from the word 'ratio'. So, rational numbers are well related to the concept of fractions which represent ratios. In other words, If a number can be expressed as a fraction where both the numerator and the denominator are integers, the number is a rational number.

Rational Numbers Definition

A rational number is a number that is of the form p/q where p and q are integers and q is not equal to 0. The set of rational numbers is denoted by Q. Observe the following figure which defines a rational number.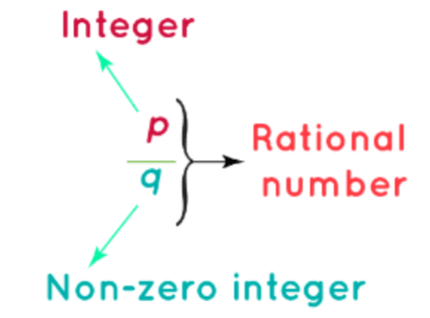

Examples of Rational Numbers
If a number can be expressed as a fraction where both the numerator and the denominator are integers, the number is a rational number. Some examples of rational numbers are as follows.

• 56 (which can be written as 56/1)
• 0 (which is another form of 0/1)
• 1/2
• √16 which is equal to 4
• -3/4
• 0.3 or 3/10
• -0.7 or -7/10
• 0.141414... or 14/99

Types of Rational Numbers

The different types of rational numbers are given as follows.

• Integers like -2, 0, 3, etc., are rational numbers.
• Fractions whose numerators and denominators are integers like 3/7, -6/5, etc., are rational numbers.
• Terminating decimals like 0.35, 0.7116, 0.9768, etc., are rational numbers.
• Non-terminating decimals with some repeating patterns (after the decimal point) such as 0.333..., 0.141414..., etc., are rational numbers. These are popularly known as non-terminating repeating decimals.

How to Identify Rational Numbers?

Rational numbers can be easily identified with the help of the following characteristics.

• All integers, whole numbers, natural numbers, and fractions with integers are rational numbers.
• If the decimal form of the number is terminating or recurring as in the case of 5.6 or 2.141414, we know that they are rational numbers.
• In case, the decimals seem to be never-ending or non-recurring, then these are called irrational numbers. As in the case of √5 which is equal to 2.236067977499789696409173... which is an irrational number.
• Another way to identify rational numbers is to see if the number can be expressed in the form p/q where p and q are integers and q is not equal to 0.

Example: Is 0.923076923076923076923076923076... a rational number?
Solution: The given number has a set of decimals 923076 which is recurring and repeated continuously. Thus, it is a rational number.

Rational Numbers in Decimal Form

Rational numbers can also be expressed in decimal form. Do you know 1.1 is a rational number? Yes, it is because 1.1 can be written as 1.1= 11/10. Now let us talk about non-terminating decimals such as 0.333..... Since 0.333... can be written as 1/3, therefore it is a rational number. Therefore, non-terminating decimals having repeated numbers after the decimal point are also rational numbers.

Is 0 a Rational Number? 
Yes, 0 is a rational number as it can be written as a fraction of integers like 0/1, 0/-2,... etc. In other words, 0/5 = 0, 0/-2 = 0, 0/1 = 0, and so on.

List of Rational Numbers 
From the above information, it is clear that there is an infinite number of rational numbers. Hence, it is not possible to determine the whole list of rational numbers. However, a few rational numbers can be listed as 3, 4.57, 3/4, 0, -7, and so on. This shows that all natural numbers, whole numbers, integers, fractions, and decimals (terminating decimals and recurring decimal numbers) are considered to be rational numbers.

Adding and Subtracting Rational Numbers

For adding and subtracting rational numbers, we use the same rules of addition and subtraction of integers. Let us understand this with the help of an example.

Example: Solve 1/2 - (-2/3)
Solution: Let us solve this using the following steps:

• Step 1: As we simplify 1/2 - (-2/3), we will follow the rule of addition and subtraction of numbers which says that the subtraction fact can change to an addition fact and the sign of the subtrahend gets reversed. This will make it 1/2 + 2/3
• Step 2: Now, we need to add these fractions 1/2 + 2/3
• Step 3: Using the rules of addition of fractions, we will convert the given fractions to like fractions to get common denominators so that it becomes easier to add them. For this, we need to find the LCM of the denominators 2 and 3 which is 6. Then we will convert the fractions to their respective equivalent fractions which will make them 3/6 + 4/6. This will give the sum as 7/6 which can be written in the form of a mixed fraction 1¹/₆

_{Multiplying and Dividing Rational Numbers}

The multiplication and division of rational numbers can be done in the same way as fractions. To multiply any two rational numbers, we multiply their numerators and their denominators separately and simplify the resultant fraction. Let us understand this with the help of an example.

Example: Multiply 3/5 × -2/7
Solution: Let us solve this using the following steps:

• Step 1: In order to multiply 3/5 × (-2)/7, we will first multiply the numerators and then multiply the denominators.
• Step 2: In this case, when we multiply the numerators, it will be 3 × (-2) = -6.
• Step 3: When we multiply the denominators, it will be 5 × 7 = 35. Therefore, the product will be -6/35.

When we need to divide any two fractions, we multiply the first fraction (which is the dividend) by the reciprocal of the second fraction (which is the divisor). Let us understand this with the help of an example.

Example: Divide 3/5 ÷ 2/7
Solution: Let us solve this using the following steps:

• Step 1: In order to divide 3/5 ÷ 2/7, we will first write the reciprocal of the second fraction. This will make it 3/5 × 7/2
• Step 2: Now, we will multiply the numerators This will be 3 × 7 = 21.
• Step 3: Then, we will multiply the denominators, it will be 5 × 2 = 10. Therefore, the product will be 21/10 or 2¹/₁₀

Rational vs Irrational Numbers

The numbers which are NOT rational numbers are called irrational numbers. The set of irrational numbers is represented by Q´. The difference between rational and irrational numbers can be understood from the following figure and table given below.

Rational Numbers Examples

Example 1: Identify the rational numbers among the following: √4, √3, √5/2, -4/5, π, 1.41421356237309504.....
Solution: A rational number when simplified should either be a terminating decimal or a non-terminating decimal with a repeating pattern of decimals. Therefore, the rational numbers among the given numbers are √4 (which results in 2) and -4/5.

Example 2: Write the following rational number in decimal form: 1/2
Solution: The rational number 1/2 can be converted to a decimal number by dividing the numerator by the denominator. We need to divide 1 by 2 and we get 0.5