Reaction Mechanism of Coordination Complexes | Inorganic Chemistry PDF Download
Reaction Mechanism of Transition Metal Complexes – I:
Inert and Labile Complexes
The metal complexes in which the rate of ligand displacement reactions is very fast and hence show high reactivity are called as labile Complexes and this property is termed as lability. On the other hand, the metal complexes in which the rate of ligand displacement reactions is very slow and hence show less reactivity are called as inert complexes and this property is termed as inertness.
Thermodynamic stability is the measure of the extent to which the complex will form or will be transformed into another complex when the system has reached equilibrium while kinetic stability refers to the speeds at which these transformations take place. The thermodynamic stability depends upon the energy difference of the reactant and product if the product has less energy than that of the reactant, it will be more stable than the reactant. The thermodynamic stability of metal complexes is calculated by the overall formation constant. If the value of log β is more than 8, the complex is considered as thermodynamically stable.
The kinetic stability of the complex depends upon the activation energy of the reaction. If the activation energy barrier is low, the reaction will take place at a higher speed. These types of complexes are also called as kinetically unstable. If the activation energy barrier is high, the substance will react slowly and will be called as kinetically stabilized or inert. There is no correlation between thermodynamic and kinetic stability. Thermodynamically stable products may labile or inert and the vice versa is also true.
Labile and Inert Complexes on the Basis of Valence Bond Theory
According to the valence bond theory of chemical bonding, octahedral metal-complexes can be divided into two types.
- Outer orbital complexes: These complexes have sp3d2 hybridization and are generally labile in nature. Valence bond theory proposed that the bonds in sp3d2 hybridization are generally weaker than that of (n-1)d2sp3 orbitals and therefore they show labile character. For example, octahedral complexes of Mn2+, Fe2+, Cr2+ complexes show fast ligand displacement.
- Inner orbital complexes: Since d2sp3 hybrid orbitals are filled with six electron pairs donated by the ligands, dn electron of metal will occupy dxy, dyz and dxz orbitals. These d2sp3 hybrid orbitals can form both inert or labile complexes. In order to show lability, one orbital out of dxy, dyz, dxz must be empty so that it can accept another electron pair and can form seven coordinated intermediate which is a necessary step for the associative pathway of ligand displacement. On the other hand, if all the dxy, dyz, dxz orbitals contain at least one electron, it will not be able to accept electron pair from the incoming ligand and hence is expected to show inert character.
Labile and Inert Complexes on the Basis of Crystal Field Theory
Octahedral complexes react either by SN1 or SN2 mechanism in which the intermediates are five and seven-coordinated species, respectively. In both cases, the symmetry of the complex is lowered down and due to this change in crystal field symmetry, the crystal field stabilization (CFSE) value also changes. The cases for lability and inertness are:
- Labile complexes: If the CFSE value for the five or seven-membered intermediate complex is greater than that of the reactant, the complex will be of labile nature as there is zero activation energy barrier.
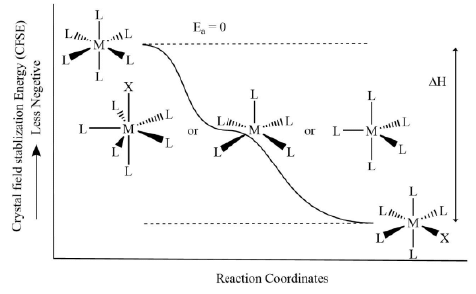 Figure 2. The reaction coordinates diagram for ligand displacement reactions in labile metal complexes.
Figure 2. The reaction coordinates diagram for ligand displacement reactions in labile metal complexes. - Inert complexes: If the CFSE value for the five or seven-membered intermediate complex is less than that of the reactant, the metal complex will be of inert nature as loss of CFSE will become the activation energy barrier.
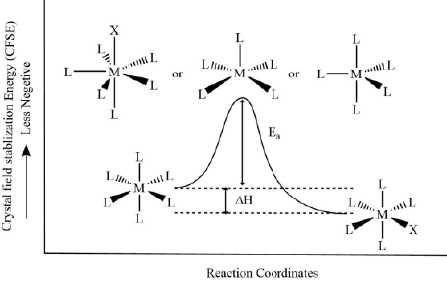 Figure 3. The general reaction coordinates diagram for ligand displacement reactions in inert metal complexes.
Figure 3. The general reaction coordinates diagram for ligand displacement reactions in inert metal complexes.
Hence, the gain of crystal field stabilization energy will make complex labile while the loss of CFSE will make complex inert. The calculation of CFSE relies upon the following assumptions:
1. All six-coordinated complexes should be treated as perfect octahedral even if the mixed ligands are present.
2. The inter-electronic repulsive forces arising from d-subshell can simply be neglected.
3. The Dq-magnitude for reacting as well as the intermediate complexes are assumed to be the same though they might have considerably different values.
4. The Jahn-Teller distortion should also be neglected in all calculations.
➤ Evidence for the lability and inertness: The ligand displacement can be dissociative or associative depending upon the nature of the reaction.
(i) For SN1 or dissociative pathway, the 5-coordinate intermediate can be trigonal-bipyramidal or squarepyramidal. However, it has been observed that the dissociative mechanism occurs through a square-pyramidal intermediate. Hence, the gain or loss of the crystal field stabilization energy can be calculated as:
CFSE gain or losss = CFSE of Squarepyramidal Intermediate – CFSE of Octahedral Reactant
If the CFSE gain-or-loss is negative, it means that activation energy is zero because it cannot be negative.
Table 1. CFSE values of high-spin (HS) and low-spin (LS) octahedral complexes undergoing ligand displacement reactions through SN1 mechanism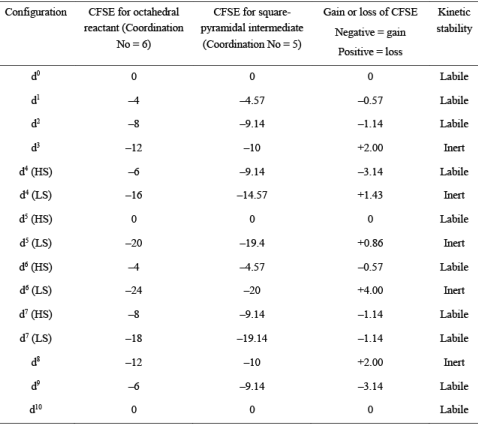
From Table 1, we can say that:
Metal complexes with d0, d1, d2, d10 are labile in nature and undergo fast ligand displacement through the dissociative pathway. High spin metal complexes with d4, d5, d6, d7 are also labile in nature and react quickly through the dissociative pathway. Low spin complexes of d7 metal ions are also found to be labile due to CFSE gain.
On the other side, d3 and d8 metal complexes are inert in nature and undergo slow ligand displacement through the dissociative pathway. Moreover, low spin complexes with d4, d5 and d6 metal complexes are also inert due to loss of CFSE during the SN1 mechanism. Using the order of CFSE loss, the reactivity can be represented as d5 > d4 > d8 > d3 > d6.
(i) For SN2 or associative pathway, the 7-coordinate intermediate can be a pentagonal-bipyramidal or octahedral wedge. However, it has been observed that the associative mechanism preferably occurs through an octahedral-wedge intermediate. Hence, the gain or loss of the CFSE can be calculated as:
CFSE gain or loss = CFSE of Octahedral-Wedge Intermediate – CFSE of Octahedral Reactant
Table 2. CFSE values of high-spin (HS) and low-spin (LS) octahedral complexes undergoing ligand displacement reactions through SN2 mechanism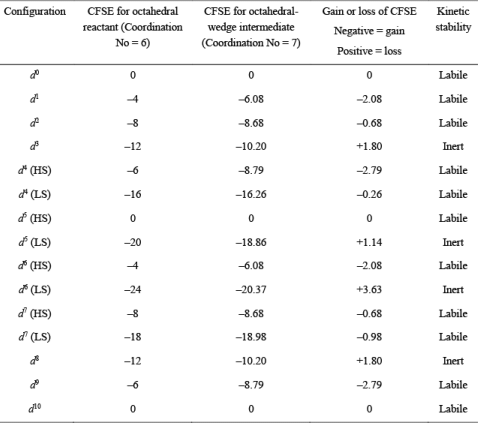 The following conclusions can be drawn from the data listed in Table 2.
The following conclusions can be drawn from the data listed in Table 2.
Metal complexes with d0, d1, d2, d10 are labile in nature and undergo fast ligand displacement through the associative pathway. High spin metal complexes with d4, d5, d6, d7 are also labile in nature and react quickly through the associative pathway. Low spin complexes of d7 metal ions are also found to be labile due to CFSE gain. It can be seen that d4 low spin are also labile in nature.
On the other side, d3 and d8 metal complexes are inert in nature and undergo slow ligand displacement through the associative pathway. Moreover, low spin complexes with d5 and d6 metal complexes are also inert due to the loss of CFSE during the SN1 mechanism. Using the order of CFSE loss, the reactivity can be represented as d5 > d8 > d3 > d6.
Factors Affecting the Kinetic Stability or Lability of Non-Transition Metal Complexes
The kinetic stability of non-transition metal complexes can be rationalized from the valence bond theory (VBT) as well as from the perspectives of crystal field theory (CFT). According to the valence bond model, all of the non-transition metal complexes are outer-orbital in nature; and therefore, are expected to show labile behavior. Similarly, the predictions of kinetic stability of octahedral complexes of non-transition metals are also labile because whatever the path is followed, associative or dissociative, the loss of CSFE will always zero. Nevertheless, the overall trend kinetic stability of transition metal complexes depends upon a number of factors discussed below.
- Charge on the central metal ion: The Lability of a complex decreases with the increasing charge on the central metal ion. For example, lability order of the following complexes:
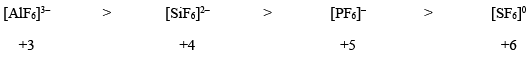
Similarly, the rate of water exchange increases with the decrease of cationic charge as: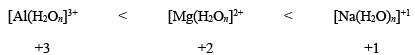
Hence, we can say that the complexes with the highest oxidation state would be most stable kinetically; while complexes with the lowest oxidation state of the metal center would be least stale kinetically. - Radii of central metal ion: It has been also observed that the kinetic stability greatly depends upon the radius of the metal center in a complex. As the radius of metal ion decreases, the lability of its complex decreases. This can be attributed to smaller metal–ligand bond, which in turn, results in stronger attraction between the metal and ligands involved. In other words, the lability of the complex is proportional to the radius of the cation. For example:
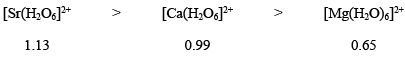
- Charge to ionic size ratio: It has been observed that for a series of octahedral complexes having the same ligands, the lability of the complexes decreases with the increase of charge to ionic size ratio. For instance, consider the replacement of H2O16 by H2O18 or simply H2O*.
[M(H2O)6]n+ + H2O∗ → [M(H2O)5(H2O∗)]n+ + H2O ...(1)
The order of lability is:
[Na(H2O)6]+1 > [Mg(H2O6]2+ > [Al(H2O6]3+
This trend can be rationalized in terms of the highest charge to ionic-size ratio for hexaaquo complex of trivalent aluminum (6.0), lowest ionic-size ratio for hexaaquo complex of trivalent sodium (1.05). Similarly,
[Sr(H2O6]2+ > [Ca(H2O6]2+ > [Mg(H2O)6]2+ - Geometry of the complex: Four-coordinated complexes, tetrahedral as well as square planar, reacts more rapidly than that of six-coordinated complexes. This can be explained in terms of lesser steric repulsion and the availability of more sites to the incoming ligand.
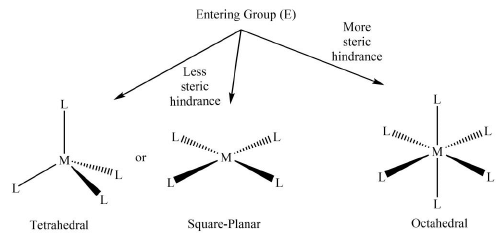 Figure 4. The general diagram comparing the steric and site availability for ligand attack in four coordinated and six coordinated complexes of non-transition metals.
Figure 4. The general diagram comparing the steric and site availability for ligand attack in four coordinated and six coordinated complexes of non-transition metals.
Now although the lability of transition metal complexes mainly depends upon the gain or loss of CFSE during the formation intermediate (what we have already discussed in this section previously), the geometry also plays some role in the same. In other words, in addition to the lability of non-transition metal complexes, ‘Figure 4’ may also be used to explain some lability profiles in transition metal complexes. For instance, the rate of exchange of CN− by 14CN− in [Ni(CN)6]2− is greater than what is observed for [Mn(CN)6]3− and [Co(CN)6]3− complexes. This can be attributed to the easy formation of an activated complex with the incoming ligand, which in turn, facilitates the removal of the previously attached ligand.
Mechanisms for Ligand Replacement Reactions
The ligand displacement in metal complexes is said to have been taken place if one of the previously attached ligands got replaced by another ligand from its coordination sphere. The scheme can be shown as:
MAnL + E → MAnE + L ...(2)
Where ligand L is the leaving group present in the complex, E is the entering ligand which is nucleophilic in nature. The coordination number of the complex remains the same.
Ligand Displacement Mechanism in Octahedral Complexes
In octahedral complexes, the replacement of the ligand can occur through dissociative, associative or by interchange mechanism. It has also been observed that most of the ligand displacement takes place through the interchange rout rather than purely associative or dissociative.
- Dissociative or SN1 Mechanism (D): In this mechanism, first of all, a metal-ligand bond breaks and the coordination number of the complex reduces from six to five forming a penta-coordinated intermediate complex. After that, the entering group attacks this intermediate and the coordination number again gets restored to six giving octahedral geometry. The whole process can be shown as
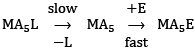 ...(3)
...(3)
The first step is the slow step and hence it is also the rate-determining step for the process. The overall rate is:
Rate = k[MA5L] ...(4)
The reaction is of the first order and is independent of the concentration of the entering ligand. These types of reactions are also called as the unimolecular nucleophilic substitution or SN1 reactions.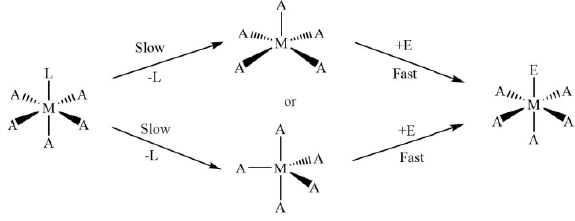 Figure 5. Pathway for ligand displacement reactions in octahedral metal complexes through SN1.
Figure 5. Pathway for ligand displacement reactions in octahedral metal complexes through SN1.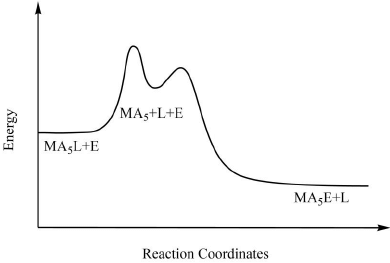 Figure 6. The typical reaction coordinate diagram for ligand displacement reactions in octahedral metal complexes through SN1 mechanism.
Figure 6. The typical reaction coordinate diagram for ligand displacement reactions in octahedral metal complexes through SN1 mechanism.
Most of the ligand substitution reactions in octahedral complexes occur through dissociative or by interchange dissociative mechanism which in turn can be evidenced by the following rules.
(i) The rate of the ligand substitution is almost independent of the concentration of the entering ligand.
(ii) The rate of the ligand substitution increases as the steric bulk around the metal center increase.
(iii) The entropy of activation, ΔS†, is positive as there are more species in activated complex than in reactant.
(iv) The volume of activation, ΔV†, for the reaction is also found to be positive. - Associative or SN2 Mechanism (A): In this mechanism, firstly the bond making with the entering group takes place, and therefore, the coordination number of the metal complex increases from six to seven forming a hepta-coordinated intermediate complex. After that, the leaving group dissociates itself from the intermediate complex completely and the coordination number of the complex again gets restored to six giving octahedral geometry. The whole process can be shown as
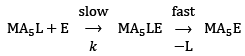 ...(5)
...(5)
The first step is the slow step and hence it is also the rate-determining step for the process. The overall rate is
Rate = k[MA5L][E] ...(6)
The reaction is of second order and it depends of the concentration of the reactant complex as well as the concentration of the entering ligand. These types of reactions are also called as bimolecular nucleophilic substitution or SN2 reactions.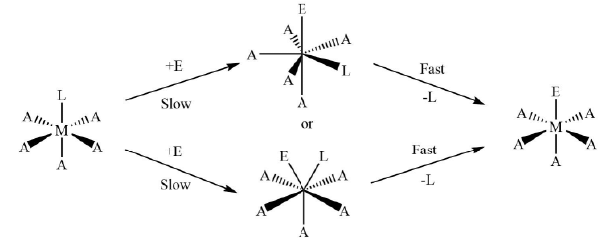 Figure 7. The general reaction mechanism for ligand displacement reactions in octahedral metal complexes through SN2 pathway.
Figure 7. The general reaction mechanism for ligand displacement reactions in octahedral metal complexes through SN2 pathway.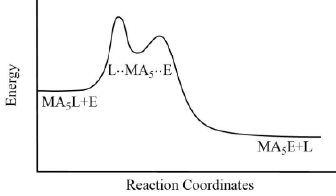 Figure 8. The typical reaction coordinate diagram for ligand displacement reactions in octahedral metal complexes through SN2 mechanism.
Figure 8. The typical reaction coordinate diagram for ligand displacement reactions in octahedral metal complexes through SN2 mechanism.
(i) The rate of the ligand substitution is increased with the concentration of the entering ligand.
(ii) The rate of the ligand substitution decreases as the steric bulk around the metal center increase.
(iii) The entropy of activation, ΔS†, is negative as there are lesser number species in activated complex than in reactant.
(iv) The volume of activation, ΔV†, for the reaction is also found to be negative. - Interchange mechanism (I): It has been observed that most of the ligand displacement reactions are neither purely associative or dissociative but follow an intermediate mechanism in which bond breaking and bond making takes place simultaneously and no penta-coordinated or hepta-coordinated intermediates have actually been isolated. These types of reactions proceed via a transition state just like in organic SN2 reactions.
MA5L + E ⟶ MA5LE ⟶ MA5E ...(7)
However, if the rate of the reaction is strongly dependent on the concentration of the entering ligand which indicates that bond making is more important in determining the rate of the reaction than the displacement is said to have been taken place via interchange associative or Ia mechanism. On the other hand, if the rate of the reaction is almost independent of the concentration of the entering ligand which clearly indicates that bond breaking is more important in determining the rate of the reaction than the displacement is said to have been taken place via interchange dissociative or Id mechanism.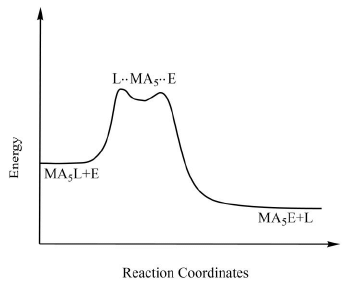 Figure 9. The typical reaction coordinate diagram for ligand displacement reactions in octahedral metal complexes through the interchange mechanism.
Figure 9. The typical reaction coordinate diagram for ligand displacement reactions in octahedral metal complexes through the interchange mechanism.
Ligand Displacement Mechanism in Square-planar Complexes
In square-planar complexes, the ligand displacement is much more favorable through the associative route than that of dissociative which can be understood in terms of low steric crowding due to lesser coordination number. The general ligand displacement can be written as: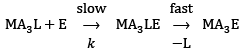 ...(8)
...(8)
The intermediate state is trigonal-bipyramidal and undergoes rapid Berry-pseudo-rotation followed by the elimination of the leaving group. Figure 10. The general reaction mechanism for ligand displacement reactions in square-planar complexes.
Figure 10. The general reaction mechanism for ligand displacement reactions in square-planar complexes.
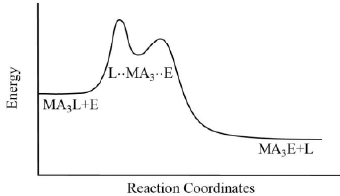 Figure 11. The typical reaction coordinate diagram for ligand displacement reactions in square-planar complexes through the associative mechanism.
Figure 11. The typical reaction coordinate diagram for ligand displacement reactions in square-planar complexes through the associative mechanism.
A more in-depth visualization of ligand displacement reactions in square-planar complexes is given below in which the involvement of Berry-pseudorotation is depicted more precisely.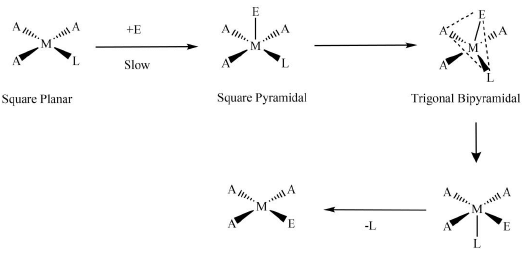 Figure 12. Involvement of Berry-pseudorotation in the ligand displacement in square-planar complexes.
Figure 12. Involvement of Berry-pseudorotation in the ligand displacement in square-planar complexes.
Formation of Complexes from Aquo Ions
The complex formation from the aquo ions yields the assembly containing metal ions with only water as ligands. These complexes are the major components in aqueous solutions of many metal salts, like metal sulphates, perchlorates and nitrates. The formula for metal-aquo complexes [M(H2O)n]z+ where the value of z generally varies from +2 to +4. The metal-aquo complexes play some very important roles in biological, industrial and environmental aspects of chemistry. Now though the homoleptic aquo complexes (only with H2O as the ligands attached) are very common, there are many other complexes that are known to have a mix of aquo and other ligand types.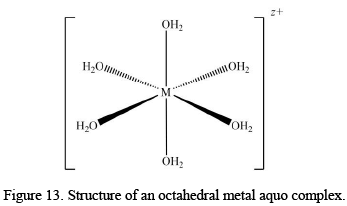
The most common stereochemistry for metal-aquo complexes is octahedral with the formula [M(H2O)6]2+ and [M(H2O)6]3+; nevertheless, some square-planar and tetrahedral complexes with the formula [M(H2O)4]2+ are also known. A general discussion on the different types and other properties is given below.
Six-Coordinated Metal-Aquo Complexes
Most of the transition metal elements from the first transition series and some alkaline earth metals form hexa-coordinated complexes when their corresponding salts are dissolved in water. Some of the most studied hexa-coordinated complexes are given below.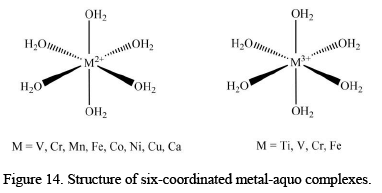
Four-Coordinated Metal-Aquo Complexes
The metal-aquo complexes that exist with coordination numbers lower than six are very uncommon but not absent from the domain. For instance, Pd2+ and Pt2+ form [M(H2O)4]2+ complexes with the squareplanar stoichiometry; and a rare tetrahedral aquo complex [Ag(H2O)4]+ is also known. Some of the most studied hexa-coordinated complexes are given below.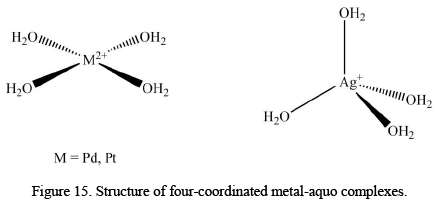
Eight and Nine Coordinated Metal-Aquo Complexes
The metal-aquo complexes of the trivalent lanthanides are eight- and nine-coordinated, which is obviously due to the large size of the metal ions. In past, the coordination number of Ln3+ ions in their aquo complexes was somewhat more or less controversial; however, nowadays, advanced characterization techniques like O17 NMR or density functional studies number of coordinated water molecules decreases from nine to eight with the decrease of the ionic radius i.e La3+ to Lu3+. Some of the most studied eight and ninecoordinated complexes are given below.
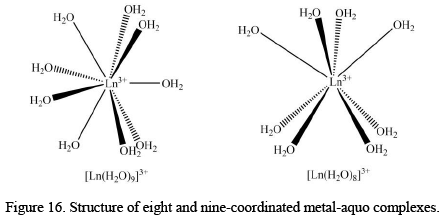
The [Ln(H2O)9]3+ ions have a trigonal triprismatic geometry with a slightly distorted D3 symmetry, while the [Ln(H2O)8]3+ ions possess a square antiprismatic geometry with a slightly distorted S8 symmetry.
Metal-Aquo Complexes with Metal-Metal Bond
There are some metal-aquo complexes which do possess metal-metal bonds. Two of the most studied examples are [Mo2(H2O)8]4+ and [Rh2(H2O)10]4+ which have eclipsed and staggered conformations, respectively. It should also be noted that metal-metal in [Mo2(H2O)8]4+ is of quadruple nature (four bond order).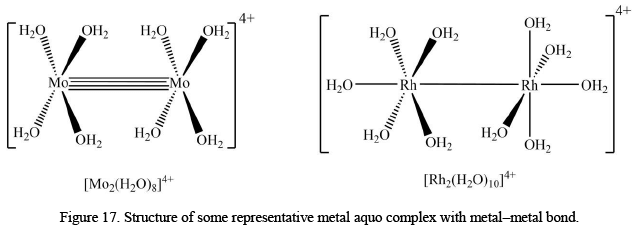
Important Reactions of Metal-Aquo Complexes
The main reactions shown by metal-aquo complexes are the electron-transfer, ligand exchange, and acid-base reactions of the O-H bonds. A general discussion on all three is given below.
- Ligand exchange: The process of ligand-exchange means the replacement of a previously coordinated H2O molecule with one from the solution. However, the detection of such phenomena is possible only by labeling the normal H2O with H2O*. The ligand-exchange generally occurs via a dissociative route, which infers that rate constants must be in accordance to the first-order kinetics. The general chemical equation for the ligandexchange in metal-aquo complexes can be given as follows:
[M(H2O)n ]z+ + H2O∗ → [M(H2O)n−1(H2O∗)]𝑧+ + H2O ...(9)
It is also worthy to mention that the above reaction would be of zero free energy change if isotopic labeling is avoided. The rate of ligand-exchange reactions is mainly affected by the charge of the species under consideration. Water-exchange rates are found to be lower for highly charged metal-aquo complexes, while the singly charged species show a much faster rate. For instance, the rates of water exchange in [Na(H2O)6]+ is 109 to what is observed in case of [Al(H2O)6]3+. However, the rates of ligand-exchange in [Al(H2O)6]3+ and [Ir(H2O)6]3+ also differs by a factor of 109 indicating that electronic configuration is also a major element in deciding the reaction kinetics. - Electron exchange: The second major types of reaction shown by the metal-aquo complexes are the electron-exchange case of electron transfer reactions. The common electron-exchange or self-exchange involves the interconversion of trivalent and bivalent metal ions via the exchange of one electron only. To track the metal ions, isotopic labeling in the self-exchange process is used and can be written as:
[M(H2O)6]2+ + [M∗(H2O)6]3+ → [M(H2O)6]3+ + [M∗(H2O)6]2+ ...(10)
Moreover, the standard redox potentials for different M2+/M3+ redox couples are: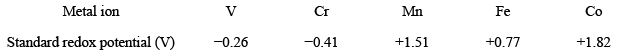 It can be clearly seen from the redox potential data that the stability of the lower oxidation state increases with the increase of the atomic number. The exceptionally large magnitude of standard reduction potential for Mn2+/Mn3+ pair is because octahedral complexes of bivalent manganese have zero crystal field stabilization energy (CFSE) but manganese(III) has −6Dq CFSE. The electron exchange rates depend mainly upon the reorganization energies. In other words, the process of electron-exchange occurs via an outer sphere electron transfer and would be slow if there is a large structural difference between the bivalent and trivalent metal centers. A detailed discussion on this topic is given in the next chapter of this book.
It can be clearly seen from the redox potential data that the stability of the lower oxidation state increases with the increase of the atomic number. The exceptionally large magnitude of standard reduction potential for Mn2+/Mn3+ pair is because octahedral complexes of bivalent manganese have zero crystal field stabilization energy (CFSE) but manganese(III) has −6Dq CFSE. The electron exchange rates depend mainly upon the reorganization energies. In other words, the process of electron-exchange occurs via an outer sphere electron transfer and would be slow if there is a large structural difference between the bivalent and trivalent metal centers. A detailed discussion on this topic is given in the next chapter of this book. - Acid-base reactions: The ionizable nature of the protons of coordinated ligand makes these metal-aquo complexes as acidic. Consider the case of aquo-complex of trivalent chromium:
[Cr(H2O)6]3+ ⇌ [Cr(H2O)5(OH)]2+ + H+ ...(11)
Therefore, in comparison to acetic acid (pKa of about 4.8) the Cr(III) aquo complex is a weaker acid (4.3). Moreover, The acidity of these aquo-complexes is also influenced by the electronic configuration; as [Ru(H2O)6]3+ (pKa = 2.7) is more acidic than [Rh(H2O)6]3+ (pKa =4), regardless of the fact that trivalent rhodium is expected to be of higher electronegativity. This can be explained in terms of the stabilization of the π-donor hydroxide ligand by the Ru3+(t2g). It has also been observed that aquo-complex of bivalent metal ions are less acidic than those of trivalent cations. The metal-hydroxo complexes so formed usually undergo olation, a condensation phenomenon that results in formation of polymeric species concentrated solutions. The properties of hydrolyzed species (formed by metal-aquo complexes) are pretty much different from the starting hexa-aquo complexes.; for instance, The rate of ligand-exchange in [Al(H2O)6]3+ is twenty thousand times faster than [Al(H2O)5OH]2+.
Finally, about one-third of all transition metals like Zr, Hf, Nb, Ta, W, Tc, Re, Os and Au; the metalaquo complexes are either unknown or rarely explained in detail. Besides, the metal-aquo complexes of tetravalent metal ions (M4+) are expected to be extraordinarily acidic; which in turn, makes their existence highly unfavorable. For instance, the aquo complex [Ti(H2O)6]4+ is unknown, but [Ti(H2O)6]3+ is well reported in many papers. The stoichiometry of aquo-complexes Zr4+ also controls the acidification as in [Zr4(OH)12(H2O)16]8+. Similarly, [VO(H2O)5]2+ is highly stable and well-characterized but [V(H2O)6]5+ is still unknown. Monovalent metal ions such as Rh+ or Cu+ rarely form isolable complexes with H2O as the ligand.
Ligand Displacement Reactions in Octahedral Complexes- Acid Hydrolysis, Base Hydrolysis
The general scheme for the ligand displacement reactions in octahedral complexes can be shown as:
MA5L + E → MA5E + L ...(12)
Where ligand L is the leaving group present in the complex, E is the entering ligand which is nucleophilic in nature. The coordination number of the complex remains the same. Moreover, if the entering group E is H2O or OH– in aqueous solution, the study of ligand displacement become more important due to extremely wide application domain. Some of the most prominent reactions in ligand substitution in six-coordinated complexes are discussed in detail.
- Acid Hydrolysis
Acid hydrolysis or aquation reactions may be defined as the reactions in which an aquo complex is formed due to the replacement of a ligand by water molecule.
It has been observed that NH3, ammines like ethylene diamine or its derivatives coordinated to Co3+ are displaced at a very small rate. Hence, displacement of the ligand other than ammonia takes place during the course of acid hydrolysis. Consider the following reaction
[Co(NH3)5L]2+ + H2O ⟶ [Co(NH3)5H2O]3+ + L– ...(13)
As reaction media is the water itself, H2O concentration (55.5 M) remains almost constant and the change in water concentration cannot be detected at all. Hence, rate law cannot be used to predict whether the reaction takes place via the associative or dissociative pathway. SN1 reactions follow first-order kinetics while SN2 reactions follow second-order kinetics. However, if the complexing agent is in the excess, SN2 reactions also become pseudo first-order reactions. Hence, it is difficult to tell whether the reaction occurs through the SN1 or SN2 mechanism.
Now, it has also been found experimentally that divalent monochloro complexes of Co(III) react at much slower than monovalent dichloro complexes.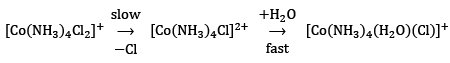 ...(14)
...(14)
and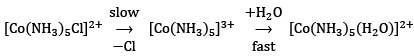 ...(15)
...(15)
The reaction (14) is 1000 times faster than reaction (15) suggesting that both of the reactions occur through dissociative or SN1 pathway. This is because the separation of a negatively charged Cl– is much more difficult from a complex of high charge density. There are also some other ground evidences which support the dissociative mechanism.
1. Solvation energy of the intermediate: The rate of acid hydrolysis in cis-[Co(en)2(NH3)Cl]2+ is five times less than in [Co(NH3)5Cl]2+ which can be explained in term of the lesser solvation energy of the intermediate. Owing to the larger chelate ring in cis-[Co(en)2(NH3)Cl]2+ the intermediate [Co(en)2(NH3)]3+ also possesses the larger size and hence less solvation energy and thus by making its formation unfavorable slows down the rate of acid hydrolysis. On the other hand, the smaller sized [Co(NH3)5]3+ complex has a smaller size and high solvation energy making its formation more favorable. Thus, by comparing the rate of acid hydrolysis in cis[Co(en)2(NH3)Cl]2+ and [Co(NH3)5Cl]2+, we can conclude that chelation stability is somewhat less important than that of the extent of solvation the intermediate undergoes in this case.
2. Steric Hindrance: The rate of acid hydrolysis in cis-[Co(en)2(NH3)Cl]2+ is smaller in cis[Co(pn)2(NH3)Cl]2+. The concept of solvation energy of the intermediate would give just the opposite order as the [Co(pn)2(NH3)]3+ is larger and has less solvation energy. However, after the dissociation of Cl–, the gain of steric relief is much greater in cis-[Co(pn)2(NH3)Cl]2+ due to bulky groups. It has been observed that the rate becomes almost double as the ethylenediamine (en) is replaced by propylene diamine group in cis[Co(en)2(NH3)Cl]2+.
3. Effect of the leaving group: The rate of acid hydrolysis is directly proportional to ease of the breaking of the bond between the metal ion and the leaving group. Batter the leaving group faster is the acid hydrolysis rate. Consider the reaction:
[Co(NH3)5L]2+ + H2O ⟶ [Co(NH3)5(H2O)]2+ + L− ...(16)
The rate of aquation is different for different L. For example, consider the acid hydrolysis of the following
[Co(NH3)5I]2+ > [Co(NH3)5Cl]2+ > [Co(NH3)5SCN]2+ > [Co(NH3)5(NO2)]2+ ...(17)
The nature of the leaving group has a pronounced effect on the aquation rate as the bond breaking is the ratedetermining step. The reactivity of the leaving group decreases in the order:
HCO3− > NO3− > I− > Br− > Cl− > SO42− > F− > CH3COO− > SCN− > NO2− - Base Hydrolysis
Base hydrolysis reactions may be defined as the reactions in which a hydroxo complex is formed due to the replacement of a ligand by hydroxyl ion.
Base hydrolysis reactions occur in solutions having pH greater than ten. Consider the following reaction
[Co(NH3)5Cl]2+ + OH− ⟶ [Co(NH3)5(OH)]2+ + X− ...(18)
In order to predict whether the reaction takes place via the associative or dissociative pathway, the value of the rate constant and reaction order must be examined very carefully. The possibility of a simple SN1 mechanism can be ruled out on the basis of an exceptionally fast rate of the reaction at higher pH. If the base hydrolysis had taken place via simple SN1 pathway, mono-chloro complexes of Co(III) would not have shown such fast rates as the rate-determining step involves the dissociation on Cl– from [Co(NH3)5Cl]2+ is quite slow due to higher charge on the complex. Moreover, at low or moderate concentrations, the rate of the reaction also depends upon the concentration OH– ions which doesn’t go well according to SN1 pathway. The proposed SN2 mechanism for base hydrolysis can be given as: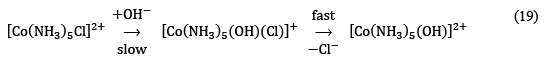
Hence, the rate law for the reaction should be given by:
Rate = k[Complex][OH–] ...(20)
However, the rate of reaction becomes independent of OH– at high concentration and the reaction starts to follow first-order kinetics. Furthermore, it has also been observed that the ligands like NCS–, N3–, NO2– are as strong nucleophile as OH– and hence are expected to show almost the same rate of hydrolysis of Co(III) amine complexes but these ligands show very slow displacement rate and is independent of the concentration of these ligands. SN2 pathway could not explain why the rate of hydrolysis of Co(III) amine complexes depends only upon OH– but not on ligands like NCS–, N3–, NO2–. Hence, the exact mechanism must be sought elsewhere.
The whole process can successfully be explained via SN1CB or substitution nucleophilic unimolecular conjugate base mechanism as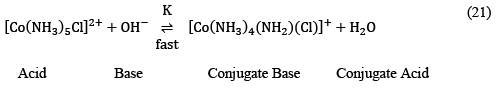
The equilibrium constant is given by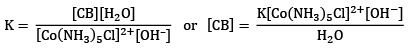
The conjugate base as obtained is more labile than the original complex [Co(NH3)5Cl]2+ and hence undergoes SN1 dissociative pathway by losing Cl– and gives penta-coordinated intermediate.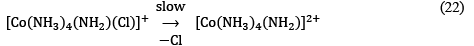
The above step is the rate-determining step.
[Co(NH3)4(NH2)]2+ + H2O ⟶ [Co(NH3)5(OH)]2+ ...(23)
There are some ground evidences which support dissociative mechanism through the formation conjugate base.
1. Hydrolysis of the complex-ions without acidic protons: The complexes like [Co(CN)5Br]3–, which do not have N–H hydrogens undergo hydrolysis much slowly in basic solutions at a rate which is almost independent the OH– concentration over a wide range. Hence, the acidic proton is a must.
2. Hydrolysis of [Co(NH3)5Cl]2+ by nucleophiles with same strength as OH–: Although the anions like NCS–, N3−, NO2− are as strong nucleophile as OH– yet they do not show fast hydrolysis of [Co(NH3)5Cl]2+ because these anions are much weaker base than that of OH– and hence unable to extract the acidic proton from the complex to form conjugate base. Therefore, the hydrolysis of [Co(NH3)5Cl]2+ by NCS–, N3−, NO2− cannot take place via SN1CB mechanism and takes place possible either via simple SN1 or SN2 pathway.
3. Hydrolysis of anionic complexes: Consider the base hydrolysis of anionic complexes like [Fe(CN)5(NH3)]3– which have acidic proton in NH3 but also have a high negative charge. In these types of complexes, the rate of hydrolysis is considerably slow and independent of the OH– ion concentration which may be attributed to the highly unfavorable formation on the conjugate base.
Racemization of Tris Chelate Complexes
The tris chelate metal complexes exist in two enantiomeric forms, called as Λ and Δ configurations.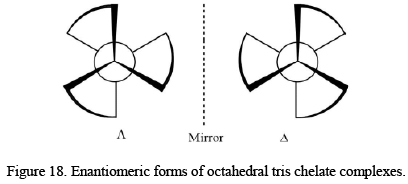 The point group symmetry for the above system D3. There are also geometrical isomers when the bidentate ligands are unsymmetrical in nature like glycinato. The total number isomer, in that case, is four as:
The point group symmetry for the above system D3. There are also geometrical isomers when the bidentate ligands are unsymmetrical in nature like glycinato. The total number isomer, in that case, is four as:
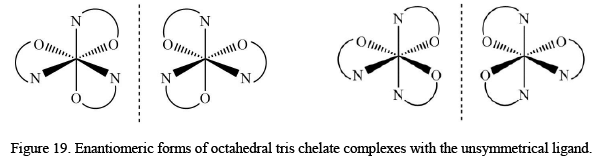
The interconversion or the racemization of tris chelate complexes in case symmetrical ligands can take place via with or without the rupturing of the metal-ligand bond.
- Racemization without the breakage of metal-ligand bond: The two most common processes suggested for the interconversion of the two enantiomeric forms are the trigonal or Bailer twist and the rhombic or Ray-Dutt twist. Both of the processes can be visualized from the following mechanism.
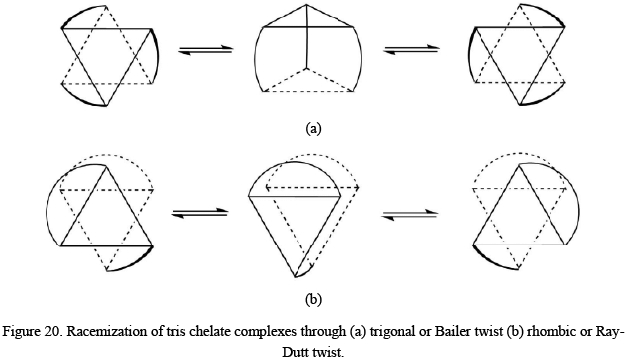 The Bailar twist mechanism proposes that the racemization of octahedral metal complexes with three bidentate rings normally occurs via the formation of an intermediate of trigonal prismatic symmetry (D3h point group). In honor of John C. Bailar, Jr., the inventor of the process, the pathway is called as Bailar twist. The second route is called the Ray-Dutt twist, a mechanism proposed also for the racemization of octahedral metal complexes with three bidentate chelate rings. These complexes usually adopt an octahedral geometry in their ground states and are therefore optically active. The Rây-Dutt pathway includes the formation of an intermediate species with C2v point group symmetry. The name Rây-Dutt twist is in the honor of P. C. Rây and N. K. Dutt, the inorganic chemists who suggested this mechanism.
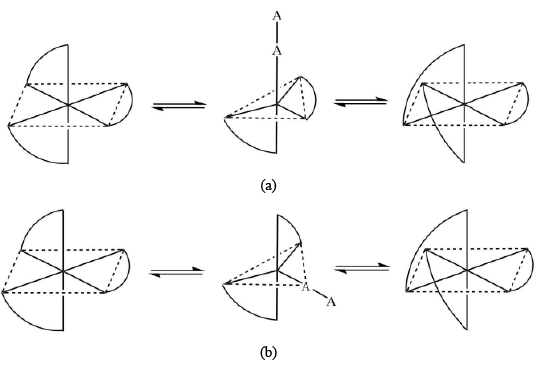
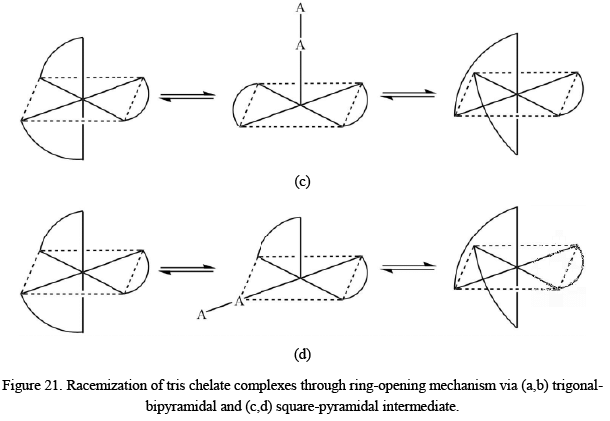
The Bailar twist mechanism proposes that the racemization of octahedral metal complexes with three bidentate rings normally occurs via the formation of an intermediate of trigonal prismatic symmetry (D3h point group). In honor of John C. Bailar, Jr., the inventor of the process, the pathway is called as Bailar twist. The second route is called the Ray-Dutt twist, a mechanism proposed also for the racemization of octahedral metal complexes with three bidentate chelate rings. These complexes usually adopt an octahedral geometry in their ground states and are therefore optically active. The Rây-Dutt pathway includes the formation of an intermediate species with C2v point group symmetry. The name Rây-Dutt twist is in the honor of P. C. Rây and N. K. Dutt, the inorganic chemists who suggested this mechanism. - Racemization with the breakage of metal-ligand bond: There are four different possible pathways suggested for the interconversion of the two enantiomeric forms of tris chelate complexes through the dissociative mechanism. After the detachment of one of the atoms of the bidentate ligand, a five-coordinated intermediate with trigonal-bipyramidal or square-pyramidal geometry is formed which converts into another enantiomer afterward. The whole process can be visualized as follows However, it is also observed that the square-pyramidal intermediate may have a weakly bonded solvent molecule at the sixth site in some cases.
Electrophilic Attack on Ligands
There is a special class of ligand substitution reactions in which ligand displacement occurs without the breaking of metal-ligand bonds. Experimental studies suggested that these reactions take place via an electrophilic attack on the ligand already attached to the metal center. Consider the preparation of [Co(NH3)5(H2O)]3+ complex from [(NH3)5–Co–CO3]+ cationic species: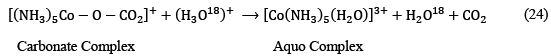
It has been observed that the no isotopically labeled oxygen is found in the aquo complex which indicates that no metal-ligand bond-breaking has actually been taken place during the course of the whole substitution process.
Mechanism: The whole process can be summed up into the following steps
(1) Electrophilic or the proton attack on the oxygen atom of the ligand bonded to the trivalent cobalt.
(2) Expulsion of CO2 and H2O to form hydroxo complex.
(3) Protonation of the hydroxo complex.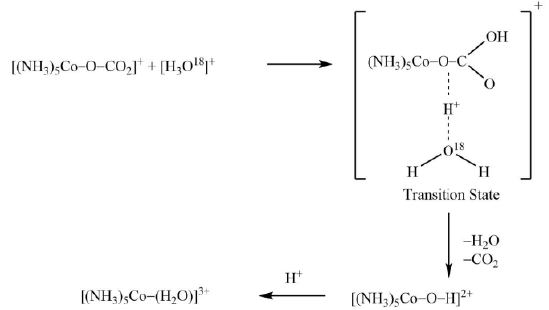 It is also worthy to mention that the reaction described above is a decarboxylation rather than the acid hydrolysis.
It is also worthy to mention that the reaction described above is a decarboxylation rather than the acid hydrolysis.
The similar behavior can be observed in the reaction of NO2− group with pentaammineaquocobalt(III) ion. When the studies involving isotopic labelling were carried out, we came to know that show that the oxygen of bound water is actually the same to what is used by NO2− to bind with metal centre. This unusual result can be explained by the following mechanism.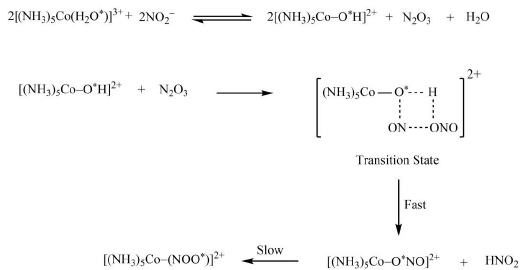
Hence, in both of the reactions given above, the displacement of previously attached ligand octahedral complexes occurs without metal-ligand bond breaking.
Problems
Q 1. How does the ligand field affect the choice between SN1 and SN2 paths in the substitution reactions of octahedral complexes? Also, explain how is this choice influenced by the basicity and π bonding capacity of a non-reacting ligand?
Q 2. Discuss the mechanism of acid hydrolysis taking the example of the octahedral complex of Co(III).
Q.3 What do you understand by SN1CB? Explain with example.
Q 4. Explain the stereochemistry of SN2 substitution reactions of octahedral complexes.
Q 5. What is base hydrolysis? Discuss the possible mechanisms.
Q 6. How does the racemization of tris chelate complexes take place?
Q 7. Explain the mechanism of nucleophilic substitution reactions in octahedral complexes.
Q 8. What are metal-aquo complexes? Also, draw and discuss the structure of eight and nine coordinated aquo complexes of trivalent lanthanide ions.
Q 9. Give a brief discussion on important reactions of metal-aquo complexes.
|
50 videos|92 docs|41 tests
|
FAQs on Reaction Mechanism of Coordination Complexes - Inorganic Chemistry
| 1. How do transition metal complexes with inert and labile properties differ in terms of their reaction mechanisms? |  |
| 2. What are the mechanisms involved in ligand replacement reactions in transition metal complexes? |  |
| 3. How do aquo ions form complexes and what is the mechanism behind it? |  |
| 4. What are the mechanisms involved in ligand displacement reactions in octahedral complexes, specifically acid and base hydrolysis? |  |
| 5. How do tris chelate complexes undergo racemization and what is the mechanism behind it? |  |
















