Real Gases | Kinetic Theory & Thermodynamics - Physics PDF Download
Andrews’ Experiment on Carbon Dioxide
Andrews’ experiment investigated the behaviour of CO2 and analyse the Pressure (P) versus volume(V) at different temperature T .
The observations are following:
- Above a temperature of about (T = 48oC), the CO2 resembles that of Ideal gas.
- As temperature is lowered, the isotherms exhibit distortion which gradually increases, which is indication of deviation from the ideal gas character.
- At 31.4oC a Kink is observed which suggests that gas can be liquified under compression.
- As temperature is lowered further, the kink spreads into a horizontal line, i.e., compression produces liquification.
From A to B , CO2 behaves as a gas. At point B, the liquification of the gas just starts. The gas condenses at constant pressure from B to , so that liquid and vapour phase co-exist. At C, the gas is completely in the liquid phase. From C to D, the slope is very steep since a liquid is almost incompressible.
Conclusion: The temperature at which it becomes possible to liquefy a gas under compression is known as critical temperature (Tc) [In Andrews’ experiment (Tc) = 48oC], corresponding pressure and volume is known as critical pressure(Pc) and critical volume (Vc) .
A gas can be liquified only if it is cooled upto or below its characteristic critical temperature.
There exist a continuity of liquid and gaseous states, i.e. they are two distinct stages of a
continuous physical phenomenon.
Van der Waals equation of state.
The van der Waals equation for real gases are given by,
For 1 mole of gas, 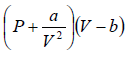 = RT
= RT
And for n mole of gas, 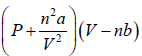 = nRT
= nRT
Assumptions for real gas:
- Gas molecules have finite size
- There are weak interaction force, which depends only upon distance between them.
- The molecular density is small and the number of collisions with the walls of the container are exactly same for point and finite size molecules.
Correction in Ideal Gas equation to achieve van der Waals gas equation of state.
Correction for finite size
If V is volume available for one mole of gas (volume of container). If size of molecule taken into account, then (V-b) ( is volume available for real gas which is less than V . b
is popularly known as co-volume, which is dependent on the nature of gas.
Example 1: If Vm is molecular volume of real gas, then prove that m b = 4NVm , if N is total number of molecule in container.

The volume available to first molecule = V
The volume available to second molecule = V - Vs
Where, Vs is volume of exclusion i.e. around any molecule, a spherical volume is Vs =
will be denied to every other molecule.
Volume of exclusion, Vs =
= 8Vm
Similarly, volume available to the Nth molecule = V - (N-1)Vs
Hence, the average volume available to each molecule is,

[As for large N , 1 can be neglected]
So, (V-b) = V - 4NVm ⇒b = 4NVm
Correction for intermolecular attraction
A molecule in the interior of the gas is on average attracted equally in all direction, so
that there is no resultant force on it. But for outermost layer closes to the surface of
container, there will be net inward force. So whenever a molecule strikes the walls of
container, the momentum exchange will be less than that for an Ideal gas.
There forces are cohesive in nature and proportional to number of molecules. So, for real
gas change in pressure is a/V2 . So for real gas pressure will be 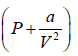
So, the gas equation reduces to 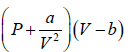 = RT
= RT
Then, P = 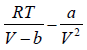
Maxwell Equal Area
James Clerk Maxwell replaced the isotherm between a and c with a horizontal line positioned so that the areas of the two hatched regions are equal (means area of adb and bec are equal). The flat line portion of the isotherm now corresponds to liquid vapor equilibrium. As shown in figure.
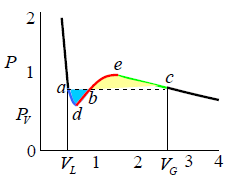
The portions a - d and c - e are interpreted as metastable states of super-heated liquid and super-cooled vapor respectively. The equal area rule can be expressed as:
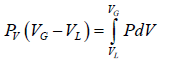
where,PV is the vapour pressure (flat portion of the curve), VL is the volume of the pure liquid phase at point a as shown in the diagram and VG is the volume of the pure gas phase at point c as shown in the diagram. The sum of these two volumes will be equal to
the total volume V .
Example 2: One mole of a certain gas is contained in a vessel of volume V . At a temperature T1 the gas pressure is p1 atm and at a temperature T2 the pressure p2 is atm. Find the van der Waals parameters for this gas.
It is given that the number of mole n =1
(i)
(ii)
from (i) and (ii)
a =
b=
Example 3: Under what pressure will carbon dioxide of molar mass M have the density ρ at the temperature T , if given gas is obeying van der Waals gas equation.
Assume M is molar mass of the carbon dioxide and V is the volume.
So, ρ = M/V
van der Wall equation (for one mole gas):
⇒ P =
⇒ P =
Critical Point
The van der Waals equation of state for a gas is given by
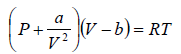
where P,V and T represent the pressure, volume and temperature respectively, a and b are constant parameters. At the critical point, all the roots of the above cubic equation are degenerate means all roots are equal.
Mathematically, the critical isotherm is the point of inflection.
On the basis of above definition, one can find the critical volume Vc , critical pressure Pc and critical temperature Tc for van der waal gas.
For van der Waals equation,
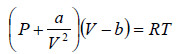
P = 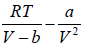 (i)
(i)
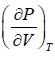 = 0, for extremum point
= 0, for extremum point
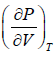 =
= 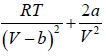 =0 at V = Vc , T = Tc (ii)
=0 at V = Vc , T = Tc (ii)
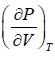 = 0, for inflection point
= 0, for inflection point
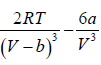 = 0 at V = Vc , T = Tc (iii)
= 0 at V = Vc , T = Tc (iii)
Solving (ii) and (iii), Vc = 3b and Tc = 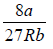
On putting the value of Vc and Tc, one can get Pc = 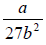
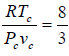 = cc which is popularly known as critical coefficient for van der Waals gas.
= cc which is popularly known as critical coefficient for van der Waals gas.
Van der Waals Equation of State and Virial Coefficient
According to virial theorem the equation of state is given by
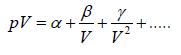 (i)
(i)
Where α ,β and γ are first, second and third virial coefficient.
For the Ideal gas, α = RT and other coefficients are zero.
Virial coefficient for Van der Waals gas
To put van der Waals equation in virial form we first rewrite it as
pV = 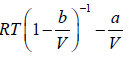
Using binomial theorem, we have
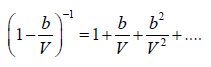
Hence
pV = 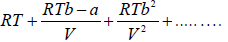 (ii)
(ii)
As it will be noted, van der Waals equation has only three virial coefficients and on comparison with equation (i) yields,
α = RT, β = RTb - a and γ = RTb2
At the Boyle’s temperature, the second virial coefficient is zero.
Hence,
RTBb - a = 0
or TB = a/Rb
From the preceding, section we recall that the critical temperature of a gas obeying van
der Waals equation of state is
Tc = 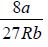
on comparing these expressions, we get
TB = 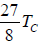 = 3.375Tc
= 3.375Tc
i.e., the Boyle’s temperature, on the basis of van der Waals equation, is 3.375 times the
critical temperature.
|
6 videos|20 docs|32 tests
|
FAQs on Real Gases - Kinetic Theory & Thermodynamics - Physics
| 1. What is the ideal gas equation and how does it relate to the van der Waals gas equation of state? |  |
| 2. How is the correction for intermolecular attraction incorporated in the van der Waals gas equation of state? |  |
| 3. What is the significance of the Maxwell Equal Area method in studying real gases? |  |
| 4. What are the Van der Waals Equation of State and Virial Coefficient in relation to real gases? |  |
| 5. Can you provide an example of how the Van der Waals Equation of State is used to describe the behavior of a real gas? |  |


 will be denied to every other molecule.
will be denied to every other molecule. = 8Vm
= 8Vm
 (i)
(i)  (ii)
(ii)


 ⇒ P =
⇒ P =  ⇒ P =
⇒ P = 


















