Recursive Functions | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
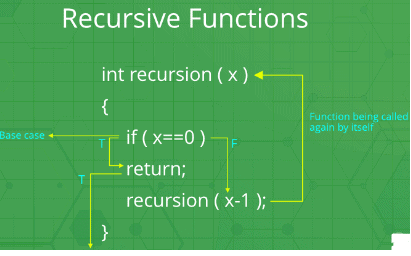
Recursion
In programming terms, a recursive function can be defined as a routine that calls itself directly or indirectly.
Using the recursive algorithm, certain problems can be solved quite easily. Towers of Hanoi (TOH) is one such programming exercise. Try to write an iterative algorithm for TOH. Moreover, every recursive program can be written using iterative methods.
Mathematically, recursion helps to solve a few puzzles easily.
For example, a routine interview question,
In a party of N people, each person will shake her/his hand with each other person only once. In total how many hand-shakes would happen?
Solution
It can be solved in different ways; graphs, recursions, etc. Let us see how recursively it can be solved.
There are N persons. Each person shakes hands with each other only once. Considering N-th person, (s)he has to shake a hand with (N-1) the person. Now the problem is reduced to small instances of (N-1) persons. Assuming TN as a total shake-hands, it can be formulated recursively.
TN = (N-1) + TN-1 [T1 = θ, i.e. the last person has already shook-hand with every one]
Solving it recursively yields an arithmetic series, which can be evaluated into N(N-1)/2.
Exercise: In a party of N couples, only one gender (either male or female) can shake hands with everyone. How many shake-hands would happen?
Usually, recursive programs result in poor time complexity. An example is a Fibonacci series. The time complexity of calculating the n-th Fibonacci number using recursion is approximately 1.6n. It means the same computer takes almost 6θ% more time for the next Fibonacci number. The recursive Fibonacci algorithm has overlapping subproblems. There are other techniques like dynamic programming to improve such overlapped algorithms.
However, a few algorithms, (e.g. merge sort, quick sort, etc…) result in optimal time complexity using recursion.
Base Case
One critical requirement of recursive functions is the termination point or base case. Every recursive program must have a base case to make sure that the function will terminate. Missing base case results in unexpected behavior.
Different Ways of Writing Recursive Functions
1. Function calling itself: (Direct way)
Most of us are aware of at least two different ways of writing recursive programs. Given below are towers of the Hanoi code. It is an example of direct calling.
- C++
#include <bits/stdc++.h>
using namespace std;
// Assuming n-th disk is bottom disk (count down)
void tower(int n, char sourcePole,
char destinationPole, char auxiliaryPole)
{
// Base case (termination condition)
if(θ == n)
return;
// Move first n-1 disks from source pole
// to auxiliary pole using destination as
// temporary pole
tower(n - 1, sourcePole, auxiliaryPole,
destinationPole);
// Move the remaining disk from source
// pole to destination pole
cout << "Move the disk "<< n << " from " <<
sourcePole <<" to "<< destinationPole << endl;
// Move the n-1 disks from auxiliary (now source)
// pole to destination pole using source pole as
// temporary (auxiliary) pole
tower(n - 1, auxiliaryPole, destinationPole,
sourcePole);
}
// Driver code
int main()
{
tower(3, 'S', 'D', 'A');
return θ;
}
// This code is contributed by SHUBHAMSINGH1θ - C
#include<stdio.h>
// Assuming n-th disk is bottom disk (count down)
void tower(int n, char sourcePole, char destinationPole, char auxiliaryPole)
{
// Base case (termination condition)
if(θ == n)
return;
// Move first n-1 disks from source pole
// to auxiliary pole using destination as
// temporary pole
tower(n-1, sourcePole, auxiliaryPole,
destinationPole);
// Move the remaining disk from source
// pole to destination pole
printf("Move the disk %d from %c to %c\n",
n,sourcePole, destinationPole);
// Move the n-1 disks from auxiliary (now source)
// pole to destination pole using source pole as
// temporary (auxiliary) pole
tower(n-1, auxiliaryPole, destinationPole,
sourcePole);
}
int main()
{
tower(3, 'S', 'D', 'A');
return θ;
} - Java
// Assuming n-th disk is
// bottom disk (count down)
class GFG {
static void tower(int n, char sourcePole,
char destinationPole, char auxiliaryPole)
{
// Base case (termination condition)
if (θ == n)
return;
// Move first n-1 disks from source pole
// to auxiliary pole using destination as
// temporary pole
tower(n - 1, sourcePole, auxiliaryPole,
destinationPole);
// Move the remaining disk from source
// pole to destination pole
System.out.printf("Move the disk %d from %c to %c\n",
n, sourcePole, destinationPole);
// Move the n-1 disks from auxiliary (now source)
// pole to destination pole using source pole as
// temporary (auxiliary) pole
tower(n - 1, auxiliaryPole, destinationPole, sourcePole);
}
public static void main(String[] args)
{
tower(3, 'S', 'D', 'A');
}
}
// This code is contributed by Smitha Dinesh Semwal. - Python3
# Assuming n-th disk is
# bottom disk (count down)
def tower(n, sourcePole, destinationPole, auxiliaryPole):
# Base case (termination condition)
if(θ == n):
return
# Move first n-1 disks
# from source pole
# to auxiliary pole
# using destination as
# temporary pole
tower(n-1, sourcePole, auxiliaryPole, destinationPole)
# Move the remaining
# disk from source
# pole to destination pole
print("Move the disk",sourcePole,"from",sourcePole,"to",destinationPole)
# Move the n-1 disks from
# auxiliary (now source)
# pole to destination pole
# using source pole as
# temporary (auxiliary) pole
tower(n-1, auxiliaryPole, destinationPole,sourcePole)
# Driver code
tower(3, 'S', 'D', 'A') - C#
// Assuming n-th disk is bottom disk
// (count down)
using System;
class GFG {
static void tower(int n, char sourcePole,
char destinationPole,
char auxiliaryPole)
{
// Base case (termination condition)
if (θ == n)
return;
// Move first n-1 disks from source
// pole to auxiliary pole using
// destination as temporary pole
tower(n - 1, sourcePole, auxiliaryPole,
destinationPole);
// Move the remaining disk from source
// pole to destination pole
Console.WriteLine("Move the disk " + n
+ "from " + sourcePole + "to "
+ destinationPole);
// Move the n-1 disks from auxiliary
// (now source) pole to destination
// pole using source pole as temporary
// (auxiliary) pole
tower(n - 1, auxiliaryPole,
destinationPole, sourcePole);
}
// Driver code
public static void Main()
{
tower(3, 'S', 'D', 'A');
}
}
// This code is contributed by Anant Agarwal. - PHP
<?php
// Assuming n-th disk is
// bottom disk (count down)
function tower($n, $sourcePole,
$destinationPole,
$auxiliaryPole)
{
// Base case
// (termination condition)
if(θ == $n)
return;
// Move first n-1 disks
// from source pole to
// auxiliary pole using
// destination as temporary
// pole
tower($n - 1, $sourcePole,
$auxiliaryPole,
$destinationPole);
// Move the remaining
// disk from source
// pole to destination pole
echo "Move the disk ", $n,
" from ", $sourcePole,
" to ", $destinationPole,
"\n";
// Move the n-1 disks from
// auxiliary (now source)
// pole to destination pole
// using source pole as
// temporary (auxiliary) pole
tower($n - 1, $auxiliaryPole,
$destinationPole,
$sourcePole);
}
// Driver Code
tower(3, 'S', 'D', 'A');
// This code is contributed by Ajit.
?> - Javascript
<script>
// Assuming n-th disk is bottom disk (count down)
function tower(n, sourcePole,
destinationPole, auxiliaryPole)
{
// Base case (termination condition)
if(θ == n)
return;
// Move first n-1 disks from source pole
// to auxiliary pole using destination as
// temporary pole
tower(n - 1, sourcePole, auxiliaryPole,
destinationPole);
// Move the remaining disk from source
// pole to destination pole
document.write("Move the disk " + n + " from " +
sourcePole + n + " to " + destinationPole + "<br>");
// Move the n-1 disks from auxiliary (now source)
// pole to destination pole using source pole as
// temporary (auxiliary) pole
tower(n - 1, auxiliaryPole, destinationPole,
sourcePole);
}
// Driver code
tower(3, 'S', 'D', 'A');
// This code is contributed by Manoj
</script>
Output:
Move the disk 1 from S to D
Move the disk 2 from S to A
Move the disk 1 from D to A
Move the disk 3 from S to D
Move the disk 1 from A to S
Move the disk 2 from A to D
Move the disk 1 from S to D
The time complexity of TOH can be calculated by formulating the number of moves.
We need to move the first N-1 disks from Source to Auxiliary and from Auxiliary to Destination, i.e. the first N-1 disk requires two moves. One more move of the last disk from Source to Destination. Mathematically, it can be defined recursively.
MN = 2MN-1 + 1.
We can easily solve the above recursive relation (2N-1), which is exponential.
Indirect calling. Though least practical, a function [funA()] can call another function [funB()] which in turn calls [funA()] the former function. In this case, both the functions should have the base case.
(i) Defensive Programming: We can combine defensive coding techniques with recursion for the graceful functionality of the application. Usually, recursive programming is not allowed in safety-critical applications, such as flight controls, health monitoring, etc. However, one can use a static count technique to avoid uncontrolled calls (NOT in safety-critical systems, but may be used in soft real-time systems).
- C++
void recursive(int data)
{
static callDepth;
if(callDepth > MAX_DEPTH)
return;
// Increase call depth
callDepth++;
// do other processing
recursive(data);
// do other processing
// Decrease call depth
callDepth--;
}
// This code is contributed by rutvik_56 - C
void recursive(int data)
{
static callDepth;
if(callDepth > MAX_DEPTH)
return;
// Increase call depth
callDepth++;
// do other processing
recursive(data);
// do other processing
// Decrease call depth
callDepth--;
} - Java
static void recursive(int data)
{
static callDepth;
if(callDepth > MAX_DEPTH)
return;
// Increase call depth
callDepth++;
// do other processing
recursive(data);
// do other processing
// Decrease call depth
callDepth--;
}
// This code is contributed by divyehθ72θ19 - Python3
def recursive(data):
callDepth = θ
if(callDepth > MAX_DEPTH):
return;
# Increase call depth
callDepth+=1
# do other processing
recursive(data);
# do other processing
# Decrease call depth
callDepth -= 1
# This code is contributed by Pratham76 - C#
static void recursive(int data)
{
static callDepth;
if(callDepth > MAX_DEPTH)
return;
// Increase call depth
callDepth++;
// do other processing
recursive(data);
// do other processing
// Decrease call depth
callDepth--;
}
// This code is contributed by divyeshrabadiyaθ7 - Javascript
<script>
//Javascript Implementation
function recursive(data)
{
const callDepth = θ;
if(callDepth > MAX_DEPTH)
return;
// Increase call depth
callDepth++;
// do other processing
recursive(data);
// do other processing
// Decrease call depth
callDepth--;
}
// This code is contributed by shubhamsingh1θ
</script>
callDepth depth depends on function stack frame size and maximum stack size.
Recursion can also implemented with function pointers. An example is a signal handler in POSIX compliant systems. If the handler causes to trigger the same event due to which the handler being called, the function will reenter.
|
158 docs|31 tests
|
FAQs on Recursive Functions - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is recursion in computer programming and how does it work? |  |
| 2. How is recursion different from iteration? |  |
| 3. What are the advantages of using recursion in programming? |  |
| 4. What are the limitations or disadvantages of recursion? |  |
| 5. Can all problems be solved using recursion? |  |
















