Reflection of Light in Spherical Mirrors | Physics for JAMB PDF Download
| Table of contents |

|
| What is Reflection? |

|
| Laws of Reflection |

|
| Types of Reflection |

|
| Image Formation by a Plane Mirror |

|
| Mirror Equation |

|
| Sign Conventions |

|
What is Reflection?
- When a ray of light falls on any object (polished, smooth, shiny object), light from the object bounces back those rays of light to our eyes and this phenomenon is known as “Reflection” or “Reflection of Light”.
- This phenomenon is what enables us to look at the world around us and is based on the property that light travels in a straight line. For example, the twinkling of stars or light reflected by a mirror.
Laws of Reflection
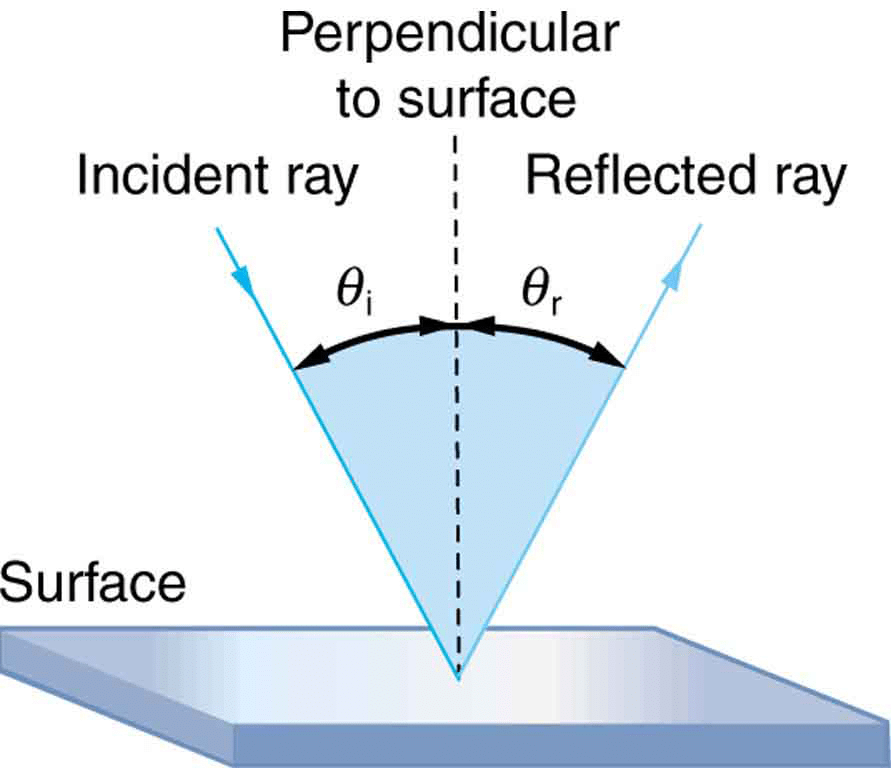
- In the diagram given above, the ray of light that approaches the mirror is known as the “Incident Ray”. The ray that leaves the mirror is known as the “Reflected Ray”.
- At the point of incidence where the incident ray strikes the mirror, a perpendicular line is drawn known as the “Normal”. This normal is what divides the incident ray and the reflected ray equally and gives us the “Angle of Incidence” (Qi) and “Angle of Reflection” (Qr).
- Hence the above information gives us the “Laws of Reflection of Light” which state that :
a. The angle of incidence is equal to the angle of reflection.
b. The incident ray, the normal ray and the reflected ray, all lie in the same plane.
Types of Reflection
There are majorly two types of reflection:
- Specular/ Regular reflection
- Diffused/ Irregular reflection
(i) Specular/Regular reflection
- A specular or regular reflection is a mirror-like reflection of rays of light. Here the rays of light which are reflected from a smooth and shiny object such as a mirror, are reflected at a definitive angle and each incident ray which is reflected along with the reflected ray has the same angle to the normal as the incident ray.
- Thus, this type of phenomenon causes the formation of an image.
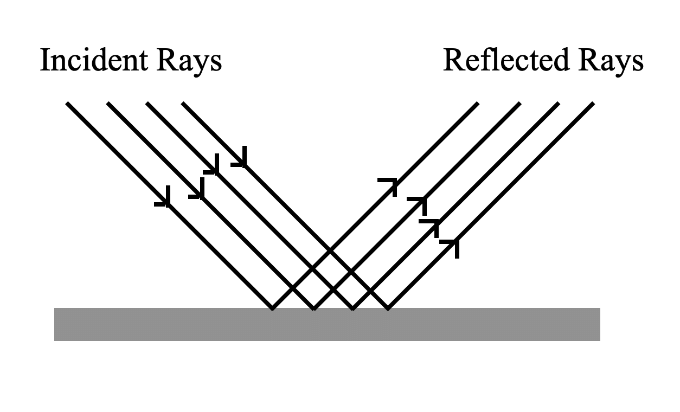 Regular Reflection
Regular Reflection
(ii) Diffused/Irregular reflection
- A diffuse or irregular reflection is a non-mirror-like reflection of light. In this type of reflection rays of light that hit an irregular object with a rough surface, are reflected back in all directions.
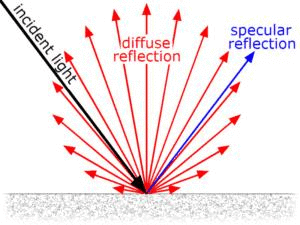 Diffuse Reflection
Diffuse Reflection - Here, the incident ray which is reflected along with the reflected ray doesn’t have the same angle to the normal as the incident ray.
- Thus, this type of reflection doesn’t form an image.
Image Formation by a Plane Mirror
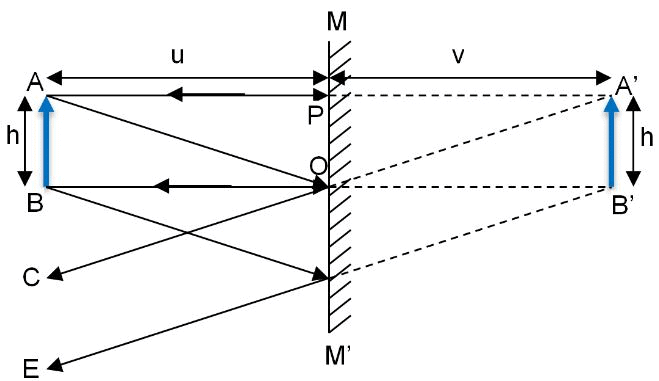
- Let us take a mirror MM’ as shown in the diagram given above. Let us suppose an object AB of size ‘h’ on the left-hand side of the mirror at a distance ‘u’.
- An incident ray of light AP from point A of the object AB falls on the mirror MM’ at point P. This incident ray AP is reflected back along the same path PA. Another ray OC falls on the mirror MM’ at a point O and is reflected along the path OC.
- Now, since reflected rays PA and OC are diverging and therefore cannot meet each other in front of the mirror, hence we extend these rays PA and OC behind the mirror by dotted lines.
- On extending these rays behind the mirror, we see that these rays meet at point A’ at a distance of V’. Therefore, A’ is the virtual image of point A of the object AB.
- Similarly, a virtual image of point B will be formed behind the mirror as B’ from the incident rays BO and BE.
- Now, to get a complete image of the object AB, we join points A and B to points A’ and B’ by a dotted line. In doing so, we find that the image A’B’ being formed is virtual, erect and of the same shape and size as the object AB; thereby giving us the characteristics of images formed by the plane mirror.
Characteristics of Images formed by Plane Mirror
(i) Images formed by a plane mirror are “Always Virtual”.
(ii) Images formed by a plane mirror are “Erect/Upright”.
(iii) Images formed by a plane mirror are of the “same shape and size” as that of an object.
Solved Examples
Ques 1: A ray of light strikes a reflective plane surface at an angle of 42º with the surface.a. Find the angle of incidence.
b. Find the angle of reflection.
c. Find the angle made by the reflected ray and the surface.
d. Find the angle made by the incident and reflected rays.
Sol: We’ll use the diagram given below to answer the question:
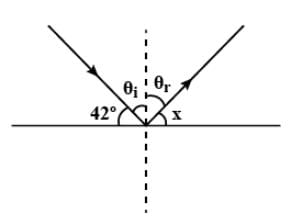
Ans: a. Angle of Incidence (Qi)= 900-420= 480
b. Angle of Reflection (Qr)= (Qi)= 480
c. x = 900-Qr = 900-480 = 420
d. Qi + Qr = 480 + 480 = 960
Ques 2: If the distance of an object and its virtual image from the focus of a convex lens of focal length f are 1 cm each, then f is
(a) 4 cm
(b) (√2+1) cm
(c) 2√2 cm
(d) (2+√2) cm
Sol:
Here, u = – (f – 1)
v = – (f + 1)
f = + f
Applying 1/v – 1/u = 1/f, we have
[1/-(f+1)] + [1/(f –1)] = 1/f
Or, f2 – 2f – 1 = 0
This gives f = (√2+1) cm
From the above observation, we conclude that, option (b) is correct.
Ques 3: A transparent rod 40 cm long is cut flat at one end and rounded to a hemispherical surface of 12 cm radius at the other end. A small object is embedded within the rod along its axis and halfway between its ends. When viewed from the flat end of the rod, the object appears 12.5 cm deep. What is its apparent depth when viewed from the curved end?
Sol:
For the flat surface: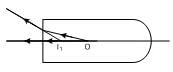
The flat surfaceReal depth of the object = 20 cm
Apparent depth = 12.5 cm
Using m = real depth / apparent depth
m = 20 / 12.5 = 1.6
For the curved surface: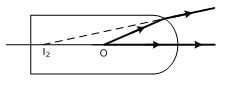
The curved surfaceWe will use, (m1/u) + (m2/v) = m2 - m1/R
u = 20 cm, R = -12 cm
So, (1.6/20) + (1/v) = (1 -1.6)/(-12)
Or, 1/v = (1/20) – (1.6/20)
Or, v = -33.3 cm
Hence the object appears 33.3 cm deep from the curved side.
Mirror Equation
It is an equation relating object distance and image distance with focal length that is known as a mirror equation. It is also known as a mirror formula.
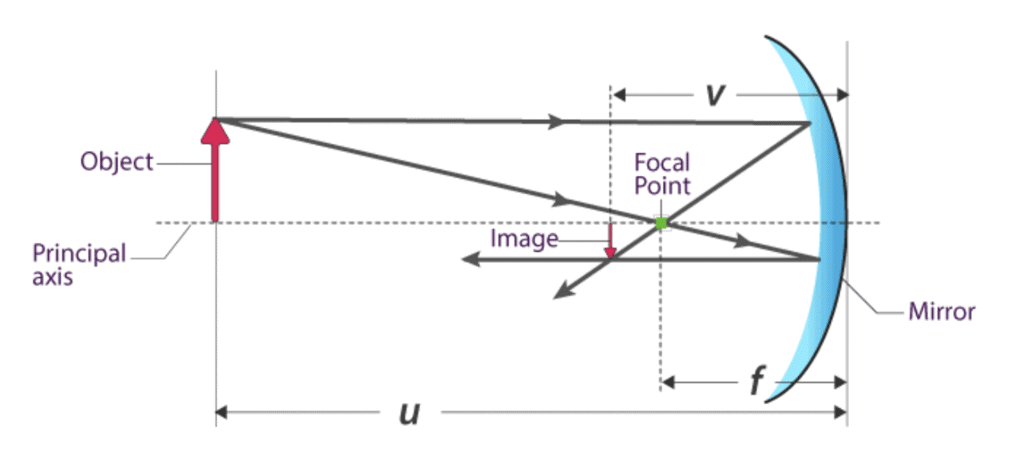
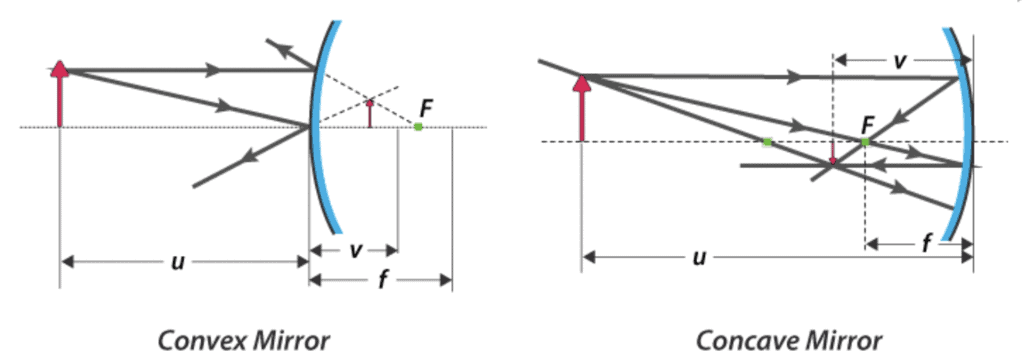
In a spherical mirror:
- The distance between the object and the pole of the mirror is called the object distance(u).
- The distance between the image and the pole of the mirror is called Image distance(v).
- The distance between the Principal focus and pole of the mirror is called Focal Length(f).
In ray optics, The object distance, image distance, and Focal length are related as,
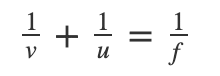
Where,
u is the Object distance
v is the Image distance
f is the Focal Length given by f=R2
R is the radius of curvature of the spherical mirror
The above formula is valid under all situations for all types of spherical mirrors (Concave and Convex) and for all object positions.
Sign Conventions

New Cartesian Sign Convention is used to avoid confusion in understanding the ray directions. Refer to the diagram for clear visualization.
- For the measurement of all the distances, the optical centre of the lens is considered.
- When the distances are measured opposite to the direction of the incident light, they are considered to be negative.
- When the distances are measured in the same direction of the incident light, they are considered to be positive.
- When the heights are measured upwards and perpendicular to the principal axis, they are considered to be positive.
- When the heights are measured downwards and perpendicular to the principal axis, they are considered to be negative.
|
260 videos|253 docs|230 tests
|
FAQs on Reflection of Light in Spherical Mirrors - Physics for JAMB
| 1. What is reflection? |  |
| 2. What are the laws of reflection? |  |
| 3. What are the types of reflection? |  |
| 4. How is an image formed by a plane mirror? |  |
| 5. What is the mirror equation? |  |





















