Regression Coefficients - Correlation & Regression, Business Mathematics & Statistics | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year PDF Download
REGRESSION COEFFICIENTS
The regression coefficient gives the value by which one variable increases for a unit increase in other variable, bXY and bYX are two coefficient of regression.
Regression coefficient of x on y or bxy can be calculated by any of the following ways—
(1) when standard deviation are given
(2) when deviations are taken from actual mean
(3) when deviations are taken from assumed mean
Regression coefficient of y on x or byx can be calculated by any of the following ways (Note that X & Y has been interchanged in the above formulas)—
(1) when standard deviations are given-
(2) when deviations are taken from actual mean
(3) when deviations are taken from assumed mean
Properties of Regression Coefficient:
The important properties of regression coefficient are given below:
1. It is denoted by b.
2. It is expressed in terms of original unit of data.
3. Between two variables (say x and y), two values of regression coefficient can be obtained. One will be obtained when we consider x as independent and y as dependent and the other when we consider y as independent and x as dependent. The regression coefficient of y on x is represented as byx and that of x on y as bxy.
4. Both regression coefficients must have the same sign. If byx is positive, bxy will also be positive and vice versa.
5. If one regression coefficient is greater than unity, then the other regression coefficient must be lesser than unity.
6. The geometric mean between two regression coefficients is equal to the coefficient of correlation, 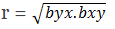
7. Arithmetic mean of both regression coefficients is equal to or greater than coefficient of correlation.
(byx + bxy)/2 = equal or greater than r
Regression coefficients are classified as:
(1) Simple, partial and multiple
(2) Positive and negative and
(3) Linear and non-linear.
Computation of Regression Coefficient:
Regression coefficient can be worked out from both un-replicated and replicated data. For calculation of regression coefficient from un-replicated data three estimates, viz., (1) sum of all observations on x and y (∑x, ∑y) variables, (2) their sum of squares (∑x2 and ∑y2) and (3) sum of products of all observations on x and y variables (∑xy).
Then regression coefficient can be worked out as follows:
byx = ∑xy – (∑x.∑y) /∑y2 – (∑y)2
bxy = ∑xy – (∑x.∑y) /∑x2 – (∑x)2
In case of replicated data, first analysis of variances and co-variances is performed and then regression coefficient is worked out as given below:
byx = Cov. (xy)/Vx, and bxy = Cov. (xy) /Vy,
where Cov = co-variance between x and y, Vx = variance of x, and Vy = variance of y.
The significance of regression coefficient is generally tested with the help of t-test.
First t is worked out as given below:
t = byx /SE (b)
The calculated value of t is compared with the table value of t at desired level of significance and appropriate degrees of freedom. If the calculated value of t is greater than table value, it is considered significant and vice versa.
The value of dependent variable can be predicated with the value of independent variable. By substituting the value of dependent variable we can get value of independent variable.
|
1334 videos|1437 docs|834 tests
|
FAQs on Regression Coefficients - Correlation & Regression, Business Mathematics & Statistics - SSC CGL Tier 2 - Study Material, Online Tests, Previous Year
| 1. What is a regression coefficient in correlation and regression analysis? |  |
| 2. How is a regression coefficient calculated? |  |
| 3. What does a positive regression coefficient indicate? |  |
| 4. What does a negative regression coefficient indicate? |  |
| 5. How do you interpret the magnitude of a regression coefficient? |  |
















