Representation of a Complex Number | Mathematics for NDA PDF Download
E. Representation Of A Complex Number
(a) Cartesian Form (Geometric Representation): Every complex number z = x + i y can be represented by a point on the cartesian plane known as complex plane (Argand diagram) by the ordered pair (x , y) .
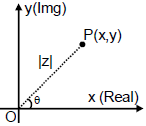
Length OP is called modulus of the complex number denoted by 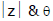 is called the argument or amplitude.
is called the argument or amplitude.
eg. 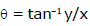 (angle made by OP with positive x-axis)
(angle made by OP with positive x-axis)
Remark :
(i) 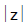 is always non negative . Unlike real numbers
is always non negative . Unlike real numbers 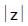 =
= 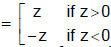 is not correct
is not correct
(ii) Argument of a complex number is a many valued function .  is the argument of a complex number then
is the argument of a complex number then 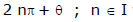 will also be the argument of that complex number. Any two arguments of a complex number differ by
will also be the argument of that complex number. Any two arguments of a complex number differ by 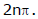
(iii) The unique value of θ such that 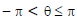 is called the principal value of the argument.
is called the principal value of the argument.
(iv) Unless otherwise stated, amp z implies principal value of the argument.
(v) By specifying the modulus & argument a complex number is defined completely. For the complex number 0 + 0 i the argument is not defined and this is the only complex number which is given by its modulus.
(vi) There exists a one-one correspondence between the points of the plane and the members of the set of complex numbers.
(b) Trigonometric / Polar Representation :
z = r (cos θ+ i sin θ) where |z| = r ; arg z = θ ; z- = r (cos θ - i sin θ)
Remark : cos θ + i sin θ is also written as CiS θ .
 are known as Euler's identities.
are known as Euler's identities.
Ex.14 Express 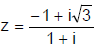 in polar form and then find the modulus and argument of z. Hence deduce the value of
in polar form and then find the modulus and argument of z. Hence deduce the value of 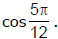
Sol.
Let –1 + i √3 = r(cosθ + i sinθ). Equating real and imaginary parts, r cosθ = -1, r sinθ= √3 .
Now r2 = 1 + 3 = 4, r = 2, cosθ = -1/2, sinθ √3/2, or θ = 2π/3 between –π and π.
Consequently, –1 + i √3 = 




It is the polar form of z. Obviously, |z| = √2 and arg z = 5/12 (principal value).



(c) Exponential Representation :
z = reiθ ; |z| = r ; arg z = θ ; z- = re- iθ
(d) Vectorial Representation :Every complex number can be considered as if it is the position vector of that point. If the point P represents the complex number z then, 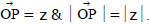
Ex.15 If (1 – i) is a root of the equation , z3 - 2 (2 - i) z2 + (4 - 5 i) z - 1 + 3 i = 0 then find the other two roots.
Sol.
z1 + z2 + z3 = 2 (2 – i) ⇒ z2 + z3 = 3 - i ( z1 = 1 - i) .......(1)
again z1 z2 z3 = 1 – 3 i
 ......(2)
......(2)
From (1) & (2) z2 = 1 & z3 = 2 – i
Ex.16 Prove that if the ratio 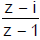 is purely imaginary then the point z lies on the circle whose centre is at the point
is purely imaginary then the point z lies on the circle whose centre is at the point 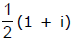 and radius is
and radius is 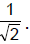
Sol. Let z = x + iy.


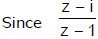 is purely imaginary, x(x – 1) + y(y – 1) = 0 or
is purely imaginary, x(x – 1) + y(y – 1) = 0 or 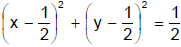
It is a circle with radius 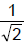 and centre
and centre 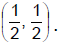
Therefore, the point z lies on a circle and the centre is 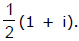
Ex.17 A function f is defined on the complex number by f (z) = (a + bi)z, where 'a' and 'b' are positive numbers. This function has the property that the image of each point in the complex plane is equidistant from that point and the origin. Given that | a + bi | = 8 and that 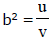 where u and v are co-primes. Find the value of (u + v).
where u and v are co-primes. Find the value of (u + v).
Sol. Given | (a + bi)z – z | = | (a + bi) z | ⇒ | z(a – 1) + biz | = | az + bzi |
= | z | | (a – 1) + bi | = | z | | a + bi |
⇒(a – 1)2 + b2 = a2 + b2 ∴ a = 1/2
since | a + bi | = 8
= a2 + b2 = 64

∴ u = 255 & v = 4 ⇒ u + v = 259
Ex.18 Show that 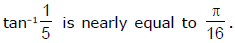
Sol.
We have (5 + i) = 26 (cosθ + isinθ), where tanq = 1/5 and therefore (5 + i)4 = 676(cos4θ + isin 4θ).
But (5 + i)4 = (24 + 10i) = 476 + 480i ; hence we have
cos 4θ = 476/676, sin 4θ = 480/676, and tan 4θ = 1, nearly.
∴ 4θ = π/4 approximately.
Ex.19 If a & b are complex numbers then find the complex numbers z1 & z2 so that the points z1 , z2 and a, b be the corners of the diagonals of a square .
Sol.
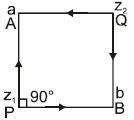
a - z1 = (b - z1) e i p/2 = i (b - z1)
a - i b = z1 (1 - i)












Ex.20 Find the square root of 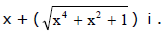
Sol.




Ex.21 On the Argand plane point 'A' denotes a complex number z1 . A triangle OBQ is made directly similar to the triangle OAM, where OM = 1 as shown in the figure . If the point B denotes the complex number z2, then find the complex number corresponding to the point 'Q' in terms of z1 & z2 .
Sol .
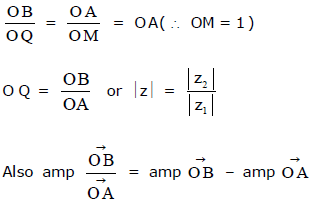
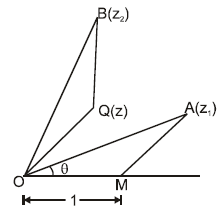
= ∠ BOM - ∠ AOM = ∠ BOM - ∠ BOQ = ∠ QOM = amp of z ( ∠ AOM = ∠ BOQ = θ) Hence complex number corresponding to the point Q = Z2/Z1
Ex.22 Compute the product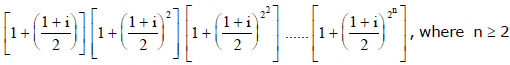
Sol. Assume  multiply numerator and denominator by (1 - z) which simplifies to
multiply numerator and denominator by (1 - z) which simplifies to 




Ex.23 Find the set of points on the complex plane such that z2 + z + 1 is real and positive (where z = x + i y) .
Sol. x2 - y2 + 2xy i + x + i y + 1 is real and positive ⇒ (x2 - y2 + x + 1) + y (2x + 1) i is real and positive ⇒ y (2x + 1) = 0 and x2 - y2 + x + 1 > 0 if y = 0 then x2 + x + 1 is always positive
complete x - axis if x = -1/2 then 3/4 - y2 >0

|
277 videos|265 docs|221 tests
|
FAQs on Representation of a Complex Number - Mathematics for NDA
| 1. What is a complex number? |  |
| 2. How are complex numbers represented graphically? |  |
| 3. What is the conjugate of a complex number? |  |
| 4. How can we add and subtract complex numbers? |  |
| 5. How can we multiply and divide complex numbers? |  |

|
Explore Courses for NDA exam
|

|

















