Representation of Graphs | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Graph and its representations
A graph is a data structure that consists of the following two components:
1. A finite set of vertices also called as nodes.
2. A finite set of ordered pair of the form (u, v) called as edge. The pair is ordered because (u, v) is not the same as (v, u) in case of a directed graph(di-graph). The pair of the form (u, v) indicates that there is an edge from vertex u to vertex v. The edges may contain weight/value/cost.
Graphs are used to represent many real-life applications: Graphs are used to represent networks. The networks may include paths in a city or telephone network or circuit network. Graphs are also used in social networks like linkedIn, Facebook. For example, in Facebook, each person is represented with a vertex(or node). Each node is a structure and contains information like person id, name, gender, and locale. See this for more applications of graph.
Following is an example of an undirected graph with 5 vertices.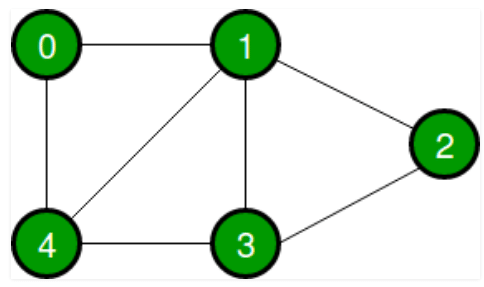
The following two are the most commonly used representations of a graph.
1. Adjacency Matrix
2. Adjacency List
There are other representations also like, Incidence Matrix and Incidence List. The choice of graph representation is situation-specific. It totally depends on the type of operations to be performed and ease of use.
Adjacency Matrix:
Adjacency Matrix is a 2D array of size V x V where V is the number of vertices in a graph. Let the 2D array be adj[][], a slot adj[i][j] = 1 indicates that there is an edge from vertex i to vertex j. Adjacency matrix for undirected graph is always symmetric. Adjacency Matrix is also used to represent weighted graphs. If adj[i][j] = w, then there is an edge from vertex i to vertex j with weight w.
The adjacency matrix for the above example graph is:

Pros: Representation is easier to implement and follow. Removing an edge takes O(1) time. Queries like whether there is an edge from vertex ‘u’ to vertex ‘v’ are efficient and can be done O(1).
Cons: Consumes more space O(V^2). Even if the graph is sparse(contains less number of edges), it consumes the same space. Adding a vertex is O(V^2) time.
Please see this for a sample Python implementation of adjacency matrix.
Adjacency List:
An array of lists is used. The size of the array is equal to the number of vertices. Let the array be an array[]. An entry array[i] represents the list of vertices adjacent to the ith vertex. This representation can also be used to represent a weighted graph. The weights of edges can be represented as lists of pairs. Following is the adjacency list representation of the above graph.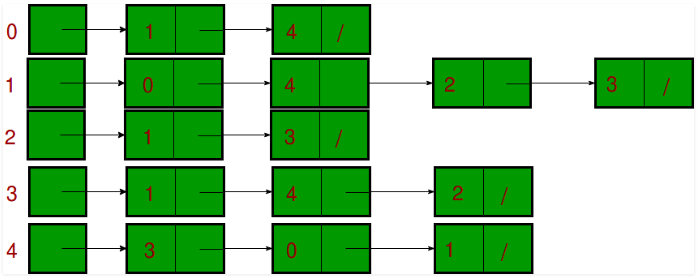
Note that in the below implementation, we use dynamic arrays (vector in C++/ArrayList in Java) to represent adjacency lists instead of the linked list. The vector implementation has advantages of cache friendliness.
C++
// A simple representation of graph using STL
#include<bits/stdc++.h>
using namespace std;
// A utility function to add an edge in an
// undirected graph.
void addEdge(vector<int> adj[], int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
// A utility function to print the adjacency list
// representation of graph
void printGraph(vector<int> adj[], int V)
{
for (int v = 0; v < V; ++v)
{
cout << "\n Adjacency list of vertex "
<< v << "\n head ";
for (auto x : adj[v])
cout << "-> " << x;
printf("\n");
}
}
// Driver code
int main()
{
int V = 5;
vector<int> adj[V];
addEdge(adj, 0, 1);
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
printGraph(adj, V);
return 0;
}
C
// A C Program to demonstrate adjacency list
// representation of graphs
#include <stdio.h>
#include <stdlib.h>
// A structure to represent an adjacency list node
struct AdjListNode
{
int dest;
struct AdjListNode* next;
};
// A structure to represent an adjacency list
struct AdjList
{
struct AdjListNode *head;
};
// A structure to represent a graph. A graph
// is an array of adjacency lists.
// Size of array will be V (number of vertices
// in graph)
struct Graph
{
int V;
struct AdjList* array;
};
// A utility function to create a new adjacency list node
struct AdjListNode* newAdjListNode(int dest)
{
struct AdjListNode* newNode =
(struct AdjListNode*) malloc(sizeof(struct AdjListNode));
newNode->dest = dest;
newNode->next = NULL;
return newNode;
}
// A utility function that creates a graph of V vertices
struct Graph* createGraph(int V)
{
struct Graph* graph =
(struct Graph*) malloc(sizeof(struct Graph));
graph->V = V;
// Create an array of adjacency lists. Size of
// array will be V
graph->array =
(struct AdjList*) malloc(V * sizeof(struct AdjList));
// Initialize each adjacency list as empty by
// making head as NULL
int i;
for (i = 0; i < V; ++i)
graph->array[i].head = NULL;
return graph;
}
// Adds an edge to an undirected graph
void addEdge(struct Graph* graph, int src, int dest)
{
// Add an edge from src to dest. A new node is
// added to the adjacency list of src. The node
// is added at the beginning
struct AdjListNode* newNode = newAdjListNode(dest);
newNode->next = graph->array[src].head;
graph->array[src].head = newNode;
// Since graph is undirected, add an edge from
// dest to src also
newNode = newAdjListNode(src);
newNode->next = graph->array[dest].head;
graph->array[dest].head = newNode;
}
// A utility function to print the adjacency list
// representation of graph
void printGraph(struct Graph* graph)
{
int v;
for (v = 0; v < graph->V; ++v)
{
struct AdjListNode* pCrawl = graph->array[v].head;
printf("\n Adjacency list of vertex %d\n head ", v);
while (pCrawl)
{
printf("-> %d", pCrawl->dest);
pCrawl = pCrawl->next;
}
printf("\n");
}
}
// Driver program to test above functions
int main()
{
// create the graph given in above fugure
int V = 5;
struct Graph* graph = createGraph(V);
addEdge(graph, 0, 1);
addEdge(graph, 0, 4);
addEdge(graph, 1, 2);
addEdge(graph, 1, 3);
addEdge(graph, 1, 4);
addEdge(graph, 2, 3);
addEdge(graph, 3, 4);
// print the adjacency list representation of the above graph
printGraph(graph);
return 0;
}
Java
// Java code to demonstrate Graph representation
// using ArrayList in Java
import java.util.*;
class Graph {
// A utility function to add an edge in an
// undirected graph
static void addEdge(ArrayList<ArrayList<Integer> > adj,
int u, int v)
{
adj.get(u).add(v);
adj.get(v).add(u);
}
// A utility function to print the adjacency list
// representation of graph
static void printGraph(ArrayList<ArrayList<Integer> > adj)
{
for (int i = 0; i < adj.size(); i++) {
System.out.println("\nAdjacency list of vertex" + i);
System.out.print("head");
for (int j = 0; j < adj.get(i).size(); j++) {
System.out.print(" -> "+adj.get(i).get(j));
}
System.out.println();
}
}
// Driver Code
public static void main(String[] args)
{
// Creating a graph with 5 vertices
int V = 5;
ArrayList<ArrayList<Integer> > adj
= new ArrayList<ArrayList<Integer> >(V);
for (int i = 0; i < V; i++)
adj.add(new ArrayList<Integer>());
// Adding edges one by one
addEdge(adj, 0, 1);
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
printGraph(adj);
}
}
Python3
"""
A Python program to demonstrate the adjacency
list representation of the graph
"""
# A class to represent the adjacency list of the node
class AdjNode:
def __init__(self, data):
self.vertex = data
self.next = None
# A class to represent a graph. A graph
# is the list of the adjacency lists.
# Size of the array will be the no. of the
# vertices "V"
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = [None] * self.V
# Function to add an edge in an undirected graph
def add_edge(self, src, dest):
# Adding the node to the source node
node = AdjNode(dest)
node.next = self.graph[src]
self.graph[src] = node
# Adding the source node to the destination as
# it is the undirected graph
node = AdjNode(src)
node.next = self.graph[dest]
self.graph[dest] = node
# Function to print the graph
def print_graph(self):
for i in range(self.V):
print("Adjacency list of vertex {}\n head".format(i), end="")
temp = self.graph[i]
while temp:
print(" -> {}".format(temp.vertex), end="")
temp = temp.next
print(" \n")
# Driver program to the above graph class
if __name__ == "__main__":
V = 5
graph = Graph(V)
graph.add_edge(0, 1)
graph.add_edge(0, 4)
graph.add_edge(1, 2)
graph.add_edge(1, 3)
graph.add_edge(1, 4)
graph.add_edge(2, 3)
graph.add_edge(3, 4)
graph.print_graph()
# This code is contributed by Kanav Malhotra
C#
// C# code to demonstrate Graph representation
// using LinkedList in C#
using System;
using System.Collections.Generic;
class Graph
{
// A utility function to add an edge in an
// undirected graph
static void addEdge(LinkedList<int>[] adj,
int u, int v)
{
adj[u].AddLast(v);
adj[v].AddLast(u);
}
// A utility function to print the adjacency list
// representation of graph
static void printGraph( LinkedList<int>[] adj)
{
for (int i = 0; i < adj.Length; i++)
{
Console.WriteLine("\nAdjacency list of vertex " + i);
Console.Write("head");
foreach (var item in adj[i])
{
Console.Write(" -> " + item);
}
Console.WriteLine();
}
}
// Driver Code
public static void Main(String[] args)
{
// Creating a graph with 5 vertices
int V = 5;
LinkedList<int>[] adj = new LinkedList<int>[V];
for (int i = 0; i < V; i++)
adj[i] = new LinkedList<int>();
// Adding edges one by one
addEdge(adj, 0, 1);
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
printGraph(adj);
Console.ReadKey();
}
}
// This code is contributed by techno2mahi
Output:
Adjacency list of vertex 0
head -> 1-> 4
Adjacency list of vertex 1
head -> 0-> 2-> 3-> 4
Adjacency list of vertex 2
head -> 1-> 3
Adjacency list of vertex 3
head -> 1-> 2-> 4
Adjacency list of vertex 4
head -> 0-> 1-> 3
Pros: Saves space O(|V|+|E|) . In the worst case, there can be C(V, 2) number of edges in a graph thus consuming O(V^2) space. Adding a vertex is easier.
Cons: Queries like whether there is an edge from vertex u to vertex v are not efficient and can be done O(V).
|
158 docs|31 tests
|
FAQs on Representation of Graphs - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is a graph in computer science engineering? |  |
| 2. What are the different representations of graphs? |  |
| 3. What is the advantage of using an adjacency matrix to represent a graph? |  |
| 4. How does an adjacency list representation save memory compared to an adjacency matrix? |  |
| 5. Which graph representation is most suitable for efficient traversal algorithms like Breadth-First Search (BFS) or Depth-First Search (DFS)? |  |
















