Effect of Temperature on Resistance & Resistivity | Physics for JAMB PDF Download
Have you ever wondered why electrical appliances heat up when used for a longer time? Resistance is a property of an electric circuit or part of a circuit that transforms electric energy into heat energy in opposing electric current. In this document, we will study about such properties as resistance and Resistivity and the effect of temperature on these in detail.
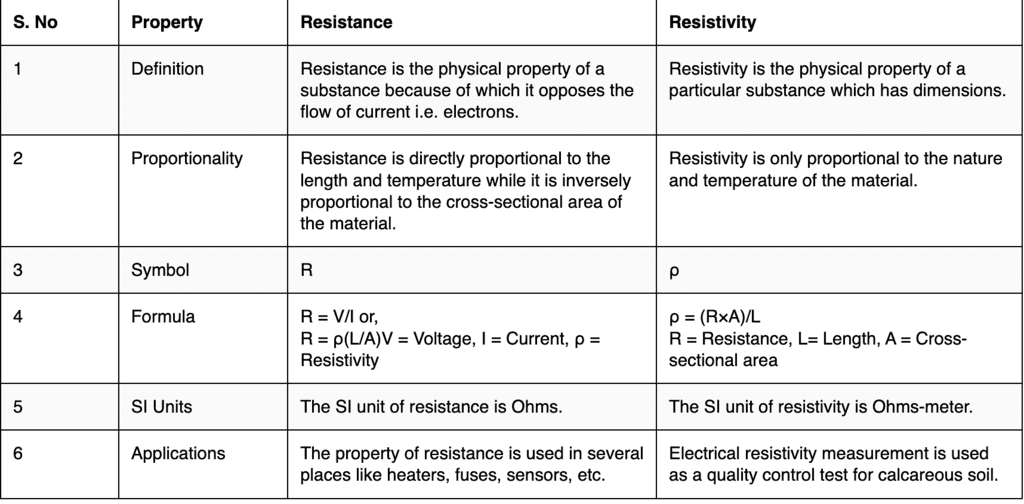
Electrical Resistance v/s Electrical Resistivity
- Resistance is the characteristic that hinders the movement of electrons, particularly the flow of electric current. It's determined by the relationship between voltage and the electric current introduced into an electronic device.
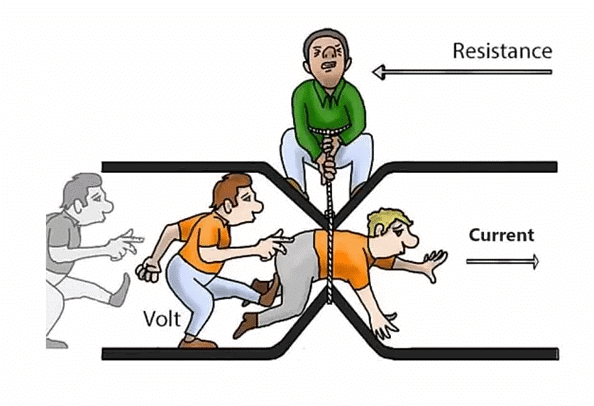 Resistance
Resistance
- Resistivity is the phenomenon of specific electrical resistance of a material or volume resistivity of a material. It can also be defined as the intrinsic property of a material that displays how the material resists the flow of current in the material. The concept can also be defined as the resistance that is displayed by a conductor which has unit length and unit area of the given cross-section.
 Resistivity
Resistivity
Temperature Dependence of Resistance
In simple terms, resistance behaves differently with temperature for different materials.
- For conductors: With increase in temperature of conductor, the number of collisions between the free electrons increases due to increase in thermal energy resulting in the random motion of electrons. These electrons find it difficult to drift in a particular direction for conduction. Hence the resistance of conductor increases as the temperature increases.
- For semiconductors: When you increase the temperature, a semiconductor's conductivity generally increases. This happens because the outermost electrons gain more energy and can leave the atom's shell.

However, there isn't a straightforward math formula that can describe how resistance changes with temperature for various materials, and it varies from one material to another.
When we increase the temperature, as a result the resistance increases. Suppose the resistance of a conductor at 0o C is R0 Ω increasing the temperature to C, the resistance becomes Rt Ω, as shown in fig.
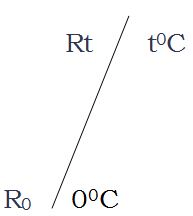
Change in resistance =ΔR
ΔR = Rt - Ro
ΔR depends upon the following three factors:
1. ΔR is directly proportional to the initial resistance, Ro
2. ΔR is directly proportional to the rise in temperature, t0C
3. ΔR depends upon the nature of the conductor.
Mathematically,

Where (α) is called the temperature co-efficient of resistances. If the resistance of the material increases on increasing the temperature such materials have a positive temperature coefficient and when on increasing the temperature and the resistance decreases such materials have a negative temperature coefficient. From the equation, we can find
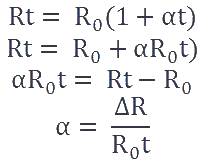
Example 1: Suppose you have a copper wire with a resistance of 10 ohms at 20 degrees Celsius. The temperature coefficient of resistance for copper is approximately 0.00393 /oC. If the temperature increases to 50oC, find the new resistance (Rt).
Solution: Substitute the values into the formula:
Rt =10Ω⋅(1+0.00393⋅(50−20))
Rt =10Ω⋅(1+0.00393⋅30)
R=10Ω⋅(1+0.1179)
R=10Ω⋅1.1179
R≈11.179Ω
So the new resistance Rt at 50oC is 11.179Ω
Example 2: Let's say you have a sample of unknown material with a resistance of 20Ω at 25oC and a resistance of 30Ω at 75oC. Find the temperature coefficient of resistance (α) for this material.
Solution:
The formula for the temperature coefficient of resistance is given by:

So, the temperature coefficient of the material is 0.01 /oC
Temperature Dependence of Resistivity
The resistivity of a material is temperature-dependent. The temperature dependence of the resistivity is different for conductors, semiconductors, and insulators. Let’s discuss how resistivity varies in conductors and insulators before discussing semiconductors.
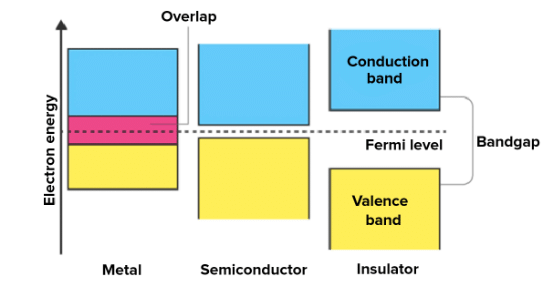
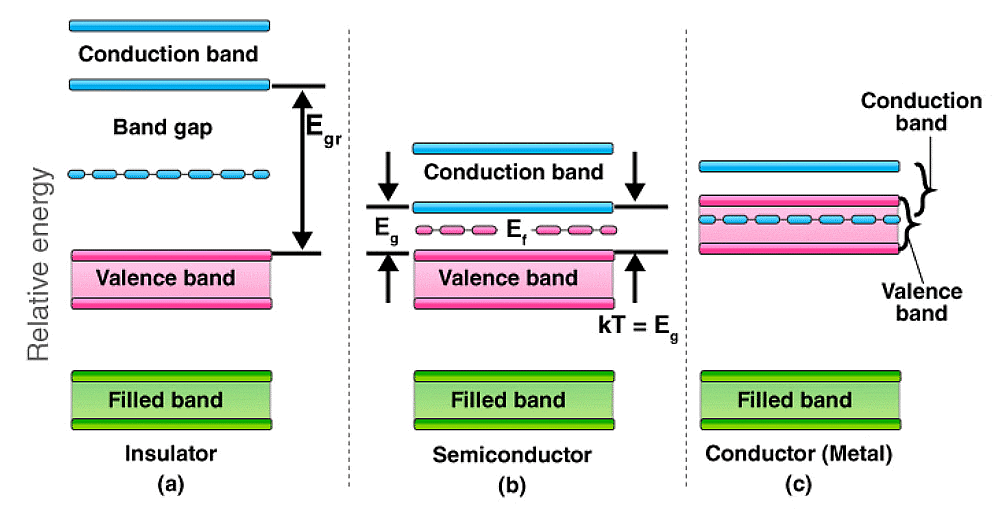 Energy Band Gaps in Materials
Energy Band Gaps in Materials
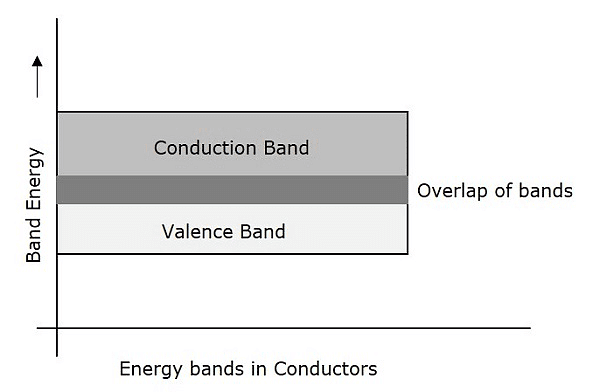
Conductors:
- In conductors, when the temperature goes up, the atoms begin to vibrate more vigorously. This increased vibration results in collisions between free electrons and other electrons.
- These collisions lead to a loss of energy from the free electrons, which are the ones responsible for carrying the electric current.
- As a result, the speed at which these electrons move, known as drift velocity, decreases due to this energy loss. This decrease in drift velocity causes the resistance of conductors, especially metals, to increase.
- In essence, as temperature rises, the resistance of the metal also goes up, which means it has a positive temperature coefficient of resistance. When the temperature is high, the resistivity of the conductor increases, and its conductivity decreases.
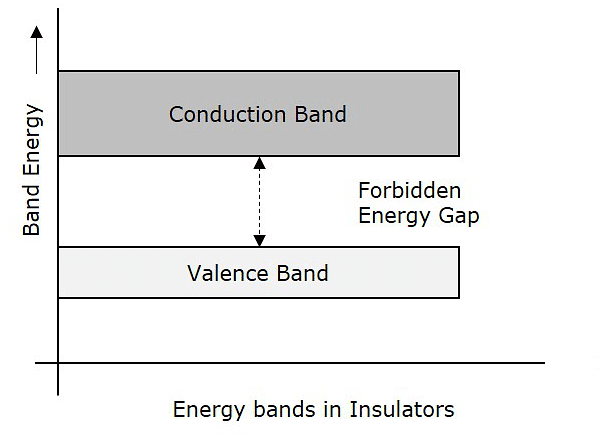
Insulators:
- Insulators shift to the conduction zone with an increase in temperature.
- The resistivity of an insulator decreases with temperature, resulting in an increase in conductivity.
- Insulators exhibit a negative temperature coefficient of resistance.
Semi-conductors:
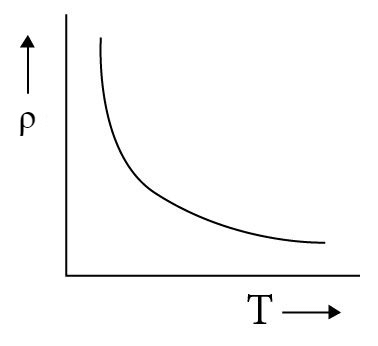
- In semiconductors, as the temperature rises, the gap between the conduction band and the valence band narrows. This increase in temperature provides the valence electrons in the semiconductor with enough energy to break free from their covalent bonds and move up to the conduction band.
- This, in turn, results in a greater number of charge carriers within the semiconductor at higher temperatures. The increased presence of these charge carriers lowers the resistance of the semiconductor.
- Consequently, as temperature increases, the semiconductor's resistance decreases, making it more conductive. Thus, at high temperatures, semiconductors display excellent conductivity.
The resistivity of materials is dependent upon the temperature of the material.
ρt = ρ0 [1 + α (T – T0)]
is the equation that defines the connection between the temperature and the resistivity of a given material. In this equation ρ0 is the resistivity at an equilibrium temperature, ρt is the resistivity at t0 C, T0 is referred to as the reference temperature and α is the temperature coefficient of resistivity.
|
263 videos|277 docs|238 tests
|
FAQs on Effect of Temperature on Resistance & Resistivity - Physics for JAMB
| 1. What is the temperature dependence of resistance? |  |
| 2. What is the effect of temperature on resistance and resistivity? |  |
| 3. How does temperature affect the conductivity of a material? |  |
| 4. What is the mathematical relationship between resistance and temperature? |  |
| 5. How does the temperature dependence of resistance impact electronic devices? |  |
















