Rings, Integral domains & Fields | Engineering Mathematics - Engineering Mathematics PDF Download
Ring – Let addition (+) and Multiplication (.) be two binary operations defined on a non empty set R. Then R is said to form a ring w.r.t addition (+) and multiplication (.) if the following conditions are satisfied:
- (R, +) is an abelian group ( i.e commutative group)
- (R, .) is a semigroup
- For any three elements a, b, c ϵ R the left distributive law a.(b+c) =a.b + a.c and the right distributive property (b + c).a =b.a + c.a holds.
Therefore a non- empty set R is a ring w.r.t to binary operations + and . if the following conditions are satisfied.
- For all a, b ϵ R, a+bϵ R,
- For all a, b, c ϵ R a+(b+c)=(a+b)+c,
- There exists an element in R, denoted by 0 such that a+0=a for all a \epsilon R
- For every a ϵ R there exists an y ϵ R such that a+y=0. y is usually denoted by -a
- a+b=b+a for all a, b ϵ R.
- a.b ϵ R for all a.b ϵ R.
- a.(b.c)=(a.b).c for all a, b ϵ R
- For any three elements a, b, c ϵ R a.(b+c) =a.b + a.c and (b + c).a =b.a + c.a. And the ring is denoted by (R, +, .).
Some Examples
- (
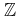 , + ) is a commutative group .(
, + ) is a commutative group .(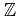 , .) is a semi-group. The distributive law also holds. So, ((
, .) is a semi-group. The distributive law also holds. So, ((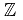 , +, .) is a ring.
, +, .) is a ring. - Ring of Integers modulo n: For a nϵ
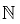 let
let 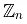 be the classes of residues of integers modulo n. i.e
be the classes of residues of integers modulo n. i.e 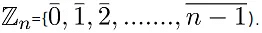
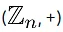 is a commutative group ere + is addition(mod n).
is a commutative group ere + is addition(mod n). 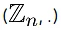 is a semi group here . denotes multiplication (mod n).
is a semi group here . denotes multiplication (mod n). - Also the distributive laws hold. So
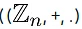 is a ring.
is a ring. - The set S = {0, 1, 2, 3, 4} is a ring with respect to operation addition modulo 5 & multiplication modulo 5.
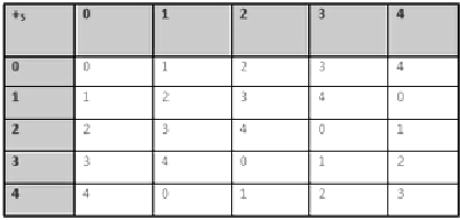
1. (S,+5) is an Abelian Group. From the above 1st composition table we can conclude that (S,+5) satisfies –
- Closure : a ∈ S ,b ∈ S => a +5 b ∈ S ; ∀ a, b ∈ S
- Associativity : (a+5b)+5c = a+5(b+5c) ; ∀ a, b, c ∈ S.
- Existence of identity 0 : (a+5b)+5c = a+5(b+5c) ; ∀ a, b, c ∈ S.
- Existence of inverse: Inverse of 0, 1, 2, 3, 4 are 0, 4, 3, 2 , 1 respectively &
- Commutative : (a+5b) = (b+5a) ; ∀ a,b ∈ S
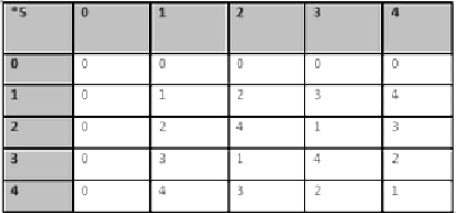
2. (S,*5) is an Semi Group. From the above 2nd composition table we can conclude that (S,*5) satisfies :
- Closure : a ∈ S ,b ∈ S => a *5 b ∈ S ; ∀ a,b ∈ S
- Associativity : (a*5b)*5c = a*5(b*5c) ; ∀ a,b,c ∈ S
3. Multiplication is distributive over addition :
(a) Left Distributive : ∀ a, b, c ∈ S :
a*5 (b +5 c)
= [ a * (b + c) ] mod 5
= [a*b + a*c] mod 5
= (a *5 b) +5 (a *5 c)
⇒ Multiplication modulo 5 is distributive over addition modulo 5.
Similarly , Right Distributive law can also be proved.
So, we can conclude that (S,+,*) is a Ring.
Many other examples also can be given on rings like 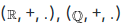 and so on.
and so on.
Before discussing further on rings, we define Divisor of Zero in A ring and the concept of unit.
Divisor of Zero in A ring –
In a ring R a non-zero element is said to be divisor of zero if there exists a non-zero element b in R such that a.b=0 or a non-zero element c in R such that c.a=0 In the first case a is said to be a left divisor of zero and in the later case a is said to be a right divisor of zero . Obviously if R is a commutative ring then if a is a left divisor of zero then a is a right divisor of zero also .
Example: In the ring  are divisors of zero since
are divisors of zero since
 and so on .
and so on .
On the other hand the rings 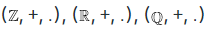 contains no divisor of zero .
contains no divisor of zero .
Units
In a non trivial ring R( Ring that contains at least to elements) with unity an element a in R is said to be an unit if there exists an element b in R such that a.b=b.a=I, I being the unity in R. b is said to be multiplicative inverse of a.
Some Important results related to Ring:
- If R is a non-trivial ring(ring containing at least two elements ) withunity I then I \neq 0.
- If I be a multiplicative identity in a ring R then I is unique .
- If a be a unit in a ring R then its multiplicative inverse is unique .
- In a non trivial ring R the zero element has no multiplicative inverse .
Types of Ring
- Null Ring: The singleton set : {0} with 2 binary operations ‘+’ & ‘*” defined by:
0+0 = 0 & 0*0 = 0 is called zero/ null ring. - Ring with Unity: If there exists an element in R denoted by 1 such that:
1*a = a* 1 = a ; ∀ a ∈ R, then the ring is called Ring with Unity. - Commutative Ring: If the multiplication in the ring R is also commutative, then ring is called a commutative ring.
- Ring of Integers: The set I of integers with 2 binary operations ‘+’ & ‘*’ is known as ring of Integers.
- Boolean Ring: A ring whose every element is idempotent, i.e. , a2 = a ; ∀ a ∈ R
- Now we introduce a new concept Integral Domain.
Integral Domain: A non -trivial ring(ring containing at least two elements) with unity is said to be an integral domain if it is commutative and contains no divisor of zero ..
Examples
The rings 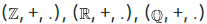 are integral domains.
are integral domains.
The ring 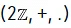 is a commutative ring but it neither contains unity nor divisors of zero. So it is not an integral domain.
is a commutative ring but it neither contains unity nor divisors of zero. So it is not an integral domain.
Next we will go to Field .
Field: A non-trivial ring R with unity is a field if it is commutative and each non-zero element of R is a unit . Therefore a non-empty set F forms a field .r.t two binary operations + and . if
- For all a, b ∈ F, a+b∈ F,
- For all a, b, c ∈ F a+(b+c)=(a+b)+c,
- There exists an element in F, denoted by 0 such that a+0=a for all a ∈ F
- For every a ∈ R there exists an y ∈ R such that a+y=0. y is usually denoted by (-a)
- a+b=b+a for all a, b ∈ F.
- a.b ∈ F for all a.b ∈ F.
- a.(b.c)=(a.b).c for all a, b ∈ F
- There exists an element I in F, called the identity element such that a.I=a for all a in F
- For each non-zero element a in F there exists an element, denoted by a-1 in F such that
aa-1 =I. - a.b =b.a for all a, b in F .
- a.(b+c) =a.b + a.c for all a, b, c in F
Examples: The rings 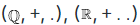 are familiar examples of fields.
are familiar examples of fields.
Some important results:
- A field is an integral domain.
- A finite integral domain is a field.
- A non trivial finite commutative ring containing no divisor of zero is an integral domain.
|
65 videos|129 docs|94 tests
|





















