Rs Aggarwal Solutions: Exercise 1C - Rational Numbers | Mathematics (Maths) Class 8 PDF Download
Q.1. Add the following rational numbers:
(i)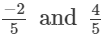
(ii)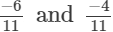
(iii)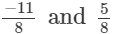
(iv)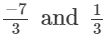
(v)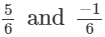
(vi)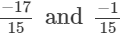
Ans.
(i)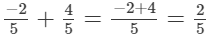
(ii)
(iii)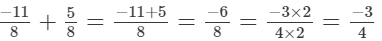
(iv)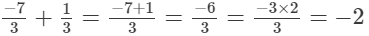
(v)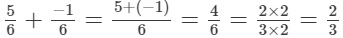
(vi)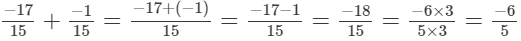
Q.2. Add the following rational numbers:
(i)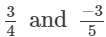
(ii)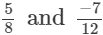
(iii)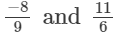
(vi)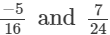
(v) 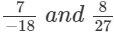
(vi) 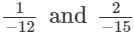
(vii) 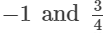
(viii) 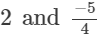
(ix) 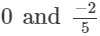
Ans.
(i) The denominators of the given rational numbers are 4 and 5.
LCM of 4 and 5 is 20.
Now,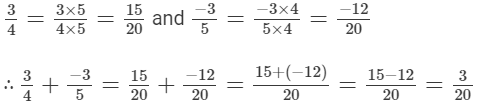 (ii)
(ii)
(ii) The denominators of the given rational numbers are 8 and 12.
LCM of 8 and 12 is 24.
Now,
(iii) The denominators of the given rational numbers are 9 and 6.
LCM of 9 and 6 is 18.
Now,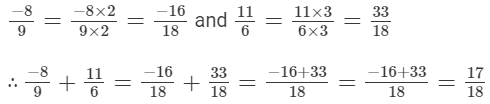
(vi) The denominators of the given rational numbers are 16 and 24.
LCM of 16 and 24 is 48.
Now,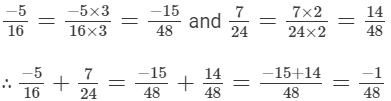
(v) We will first write each of the given numbers with positive denominators.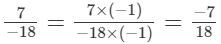
The denominators of the given rational numbers are 18 and 27.
LCM of 18 and 27 is 54.
Now,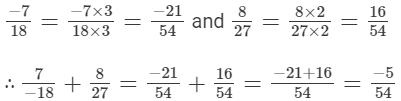
(vi) We will first write each of the given numbers with positive denominators.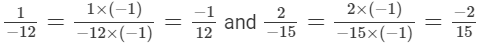
The denominators of the given rational numbers are 12 and 15.
LCM of 12 and 15 is 60.
Now,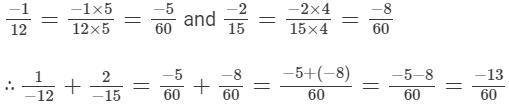
(vii) We can write - 1 as 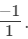
The denominators of the given rational numbers are 1 and 4.
LCM of 1 and 4 is 4.
Now,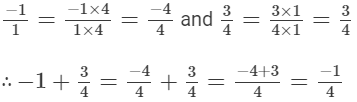
(viii) We can write 2 as 2/1.
The denominators of the given rational numbers are 1 and 4.
LCM of 1 and 4 is 4.
Now,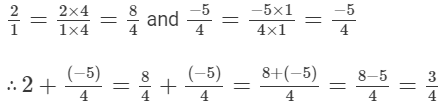
(ix) We can write 0 as 0/1.
The denominators of the given rational numbers are 1 and 5.
LCM of 1 and 5 is 5, that is, (1 × 5).
Now,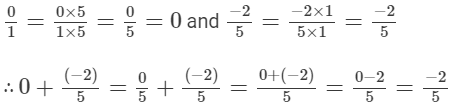
Q.3. Verify the following:
(i)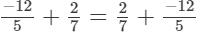
(ii)
(iii)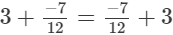
(iv)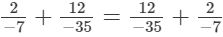
Ans.
(i) LHS = 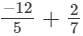
LCM of 5 and 7 is 35.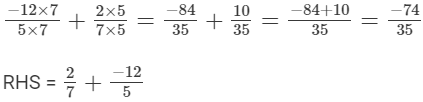
LCM of 5 and 7 is 35.
(ii)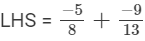
LCM of 8 and 13 is 104.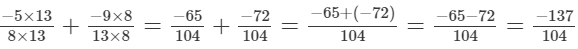
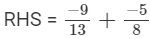
LCM of 13 and 8 is 104.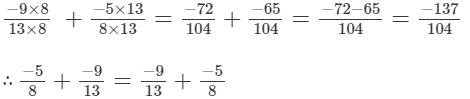
(iii) 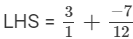
LCM of 1 and 12 is 12.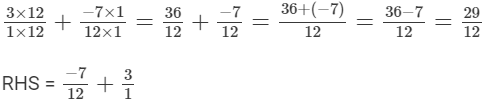
LCM of 12 and 1 is 12.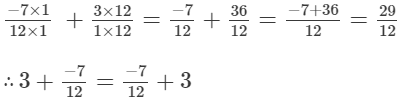
(iv)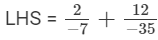
We will write the given numbers with positive denominators.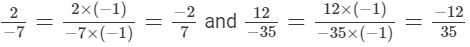
LCM of 7 and 35 is 35.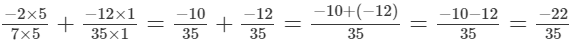
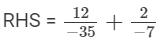
We will write the given numbers with positive denominators.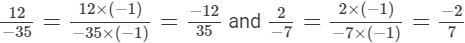
LCM of 35 and 7 is 35.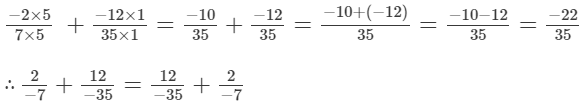
Q.4. Verify the following:
(i)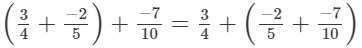
(ii)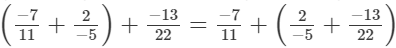
(iii)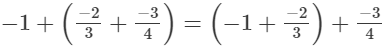
Ans.
(i)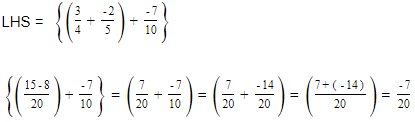
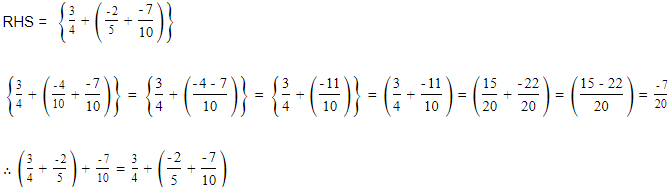
(ii)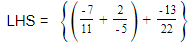
We will first make the denominator positive.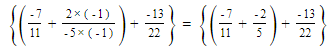

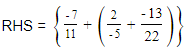
We will first make the denominator positive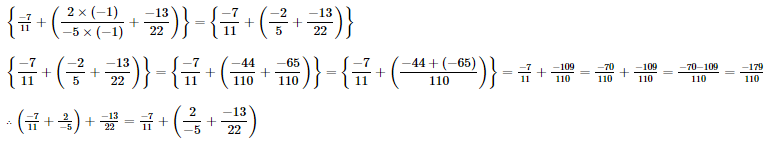
(iii)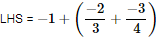
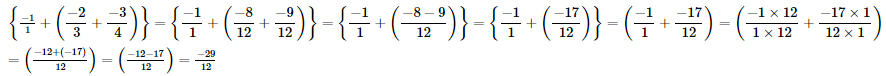
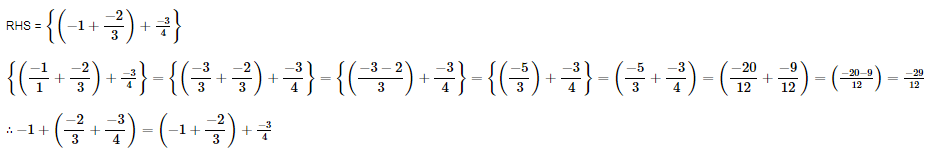
Q.5. Fill in the blanks.
(i)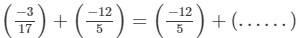
(ii)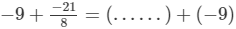
(iii)
(iv)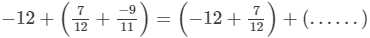
(v)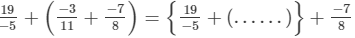
(vi)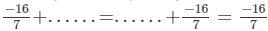
Ans.
(i) Addition is commutative, that is, a+b=b+a.
Hence, the required solution is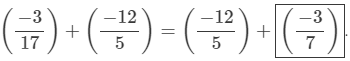
(ii) Addition is commutative, that is, a+b=b+a.
Hence, the required solution is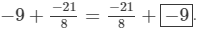
(iii) Addition is associative, that is, (a+b)+c=a+(b+c).
Hence, the required solution is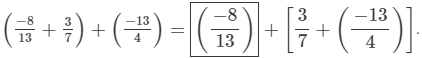
(iv) Addition is associative, that is, (a+b)+c=a+(b+c).
Hence, the required solution is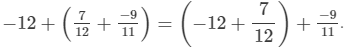
(v) Addition is associative, that is, (a+b)+c=a+(b+c).
Hence, the required solution is 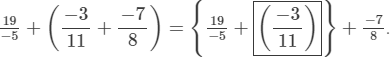
(vi) 0 is the additive identity, that is, 0+a=a.
Hence, the required solution is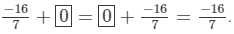
Q.6. Find the additive inverse of each of the following:
(i)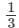
(ii)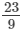
(iii) −18
(vi)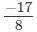
(v)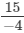
(vi)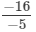
(vii)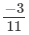
(viii) 0
(ix)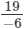
(x)
Ans.
The additive inverse of 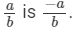 Therefore,
Therefore, 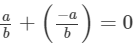
(i) Additive inverse of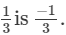
(ii) Additive inverse of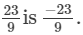
(iii) Additive inverse of -18 is 18.
(iv) Additive inverse of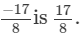
(v) In the standard form, we write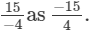
Hence, its additive inverse is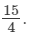
(vi) We can write: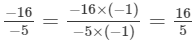
Hence, its additive inverse is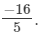
(vii) Additive inverse of 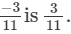
(viii) Additive inverse of 0 is 0.
(ix) In the standard form, we write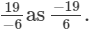
Hence, its additive inverse is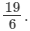
(x) We can write: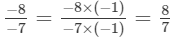
Hence, its additive inverse is 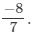
Q.7. Subtract:
(i)
(ii)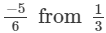
(iii)
(iv)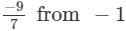
(v)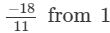
(vi)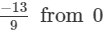
(vii)
(viii)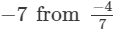
Ans.
(i)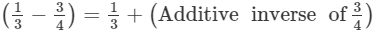
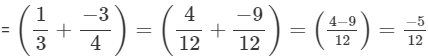
(ii)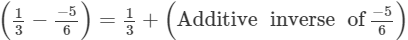
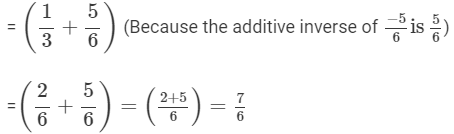
(iii)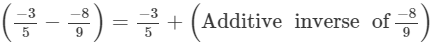
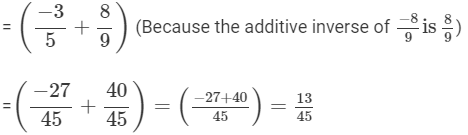
(iv)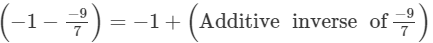
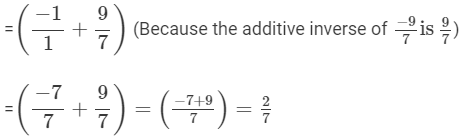
(v)
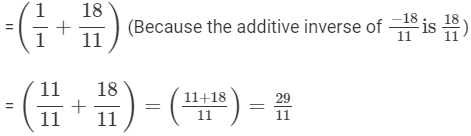
(vi)

(vii)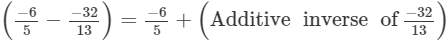
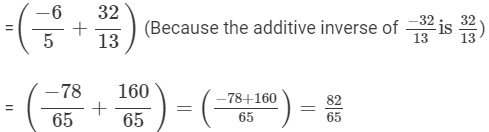
(viii)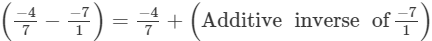
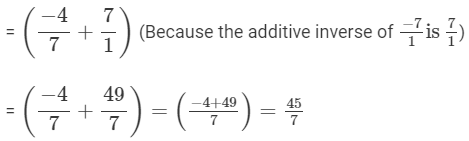
Q.8. Using the rearrangement property find the sum:
(i)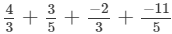
(ii)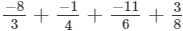
(iii)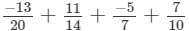
(iv)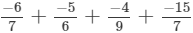
Ans.
(i)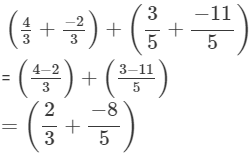
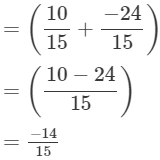
(ii)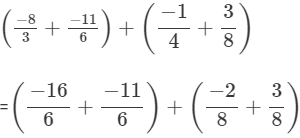
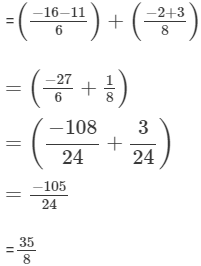
(iii)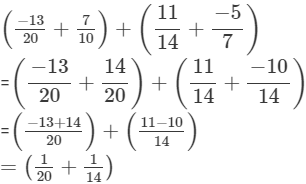
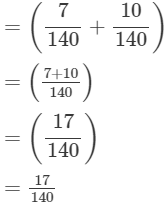
(iv)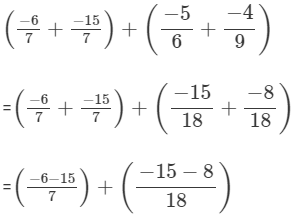
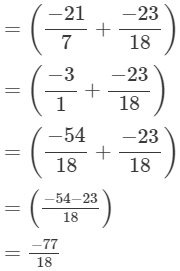
Q.9. The sum of two rational numbers is −2. If one of the numbers is 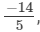 find the other.
find the other.
Ans.
Let the other number be x.
Now,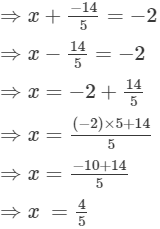
Q.10. The sum of two rational numbers is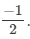 If one of the numbers is 5/6,
If one of the numbers is 5/6,
find the other.
Ans.
Let the other number be x.
Now,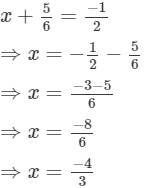
Q.11. What number should be added to  so as to get
so as to get 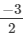 ?
?
Ans.
Let the required number be x.
Now,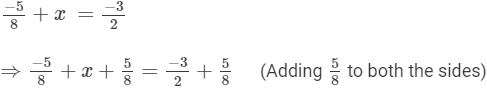
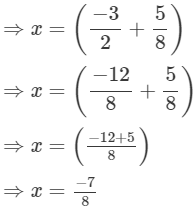
Hence, the required number is 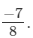
Q.12. What number should be added to −1 so as to get 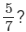
Ans.
Let the required number be x.
Now,
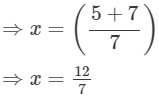
Hence, the required number is 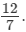
Q.13. What number should be subtracted from 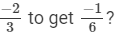
Ans.
Let the required number be x.
Now,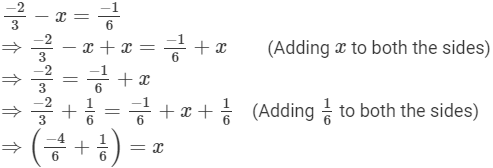

Hence, the required number is 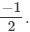
Q.14.
(i) Which rational number is its own additive inverse?
(ii) Is the difference of two rational numbers a rational number?
(iii) Is addition commutative on rational numbers?
(iv) Is addition associative on rational numbers?
(v) Is subtraction commutative on rational numbers?
(vi) Is subtraction associative on rational numbers?
(vii) What is the negative of a negative rational number?
Ans.
(i) Zero is a rational number that is its own additive inverse.
(ii) Yes Consider 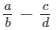 (with a, b, c and d as integers), where b and d are not equal to 0.
(with a, b, c and d as integers), where b and d are not equal to 0.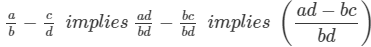
Since ad, bc and bd are integers since integers are closed under the operation of multiplication and ad−bc is an integer since integers are closed under the operation of subtraction, then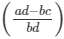
since it is in the form of one integer divided by another and the denominator is not equal to 0
Since, b and d were not equal to 0
Thus,  is a rational number.
is a rational number.
(iii) Yes, rational numbers are commutative under addition. If a and b are rational numbers, then the commutative law under addition is a+b=b+a.
(iv) Yes, rational numbers are associative under addition. If a, b and c are rational numbers, then the associative law under addition is a+(b+c)=(a+b)+c.
(v) No, subtraction is not commutative on rational numbers. In general, for any two rational numbers, (a−b) ≠ (b − a).
(vi) Rational numbers are not associative under subtraction. Therefore, a−(b−c)≠(a−b)−c.
(vii) Negative of a negative rational number is a positive rational number.
|
81 videos|423 docs|31 tests
|
FAQs on Rs Aggarwal Solutions: Exercise 1C - Rational Numbers - Mathematics (Maths) Class 8
| 1. What is the significance of rational numbers in mathematics? |  |
| 2. How do you add and subtract rational numbers? |  |
| 3. Can rational numbers be negative? |  |
| 4. What is the difference between a rational number and an irrational number? |  |
| 5. How are rational numbers used in everyday life? |  |





















