SOHCAHTOA | Mathematics for GCSE/IGCSE - Year 11 PDF Download

What is Trigonometry?

• Trigonometry is the branch of mathematics that deals with angles in triangles.
• It explores the relationships between the side lengths and angles of triangles.
• The term originates from the Greek words "trigonon," meaning 'triangle,' and "metron," meaning 'measure.'

What are Sin, Cos and Tan?

• The fundamental trigonometric functions - Sine, Cosine, and Tangent - originate from the ratios of side lengths within right-angled triangles.
• To comprehend these ratios, it is essential to assign labels to the sides of a right-angled triangle concerning a specified angle:
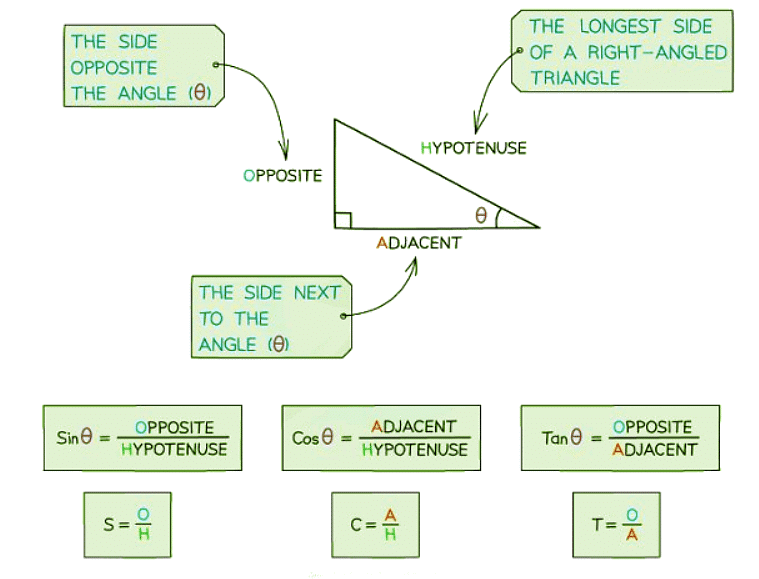
  • The longest side in a right-angled triangle is termed the hypotenuse (H) and always lies opposite the right angle.
  • If we designate one of the other angles as θ, the side opposite θ is referred to as the opposite side (O), while the side adjacent to θ is known as the adjacent side (A).
• The functions Sine, Cosine, and Tangent represent the ratios of the lengths of these sides in the following manner.

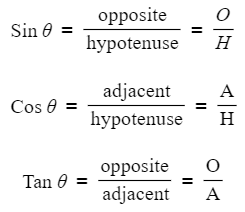
What is SOHCAHTOA?

• SOHCAHTOA is a helpful mnemonic used in trigonometry to remember trigonometric ratios.
• It stands for:
  • Sine is Opposite over Hypotenuse
  • Cosine is Adjacent over Hypotenuse
  • Tangent is Opposite over Adjacent
• In a right-angled triangle, label one angle other than the right angle and label the sides of the triangles as follows:

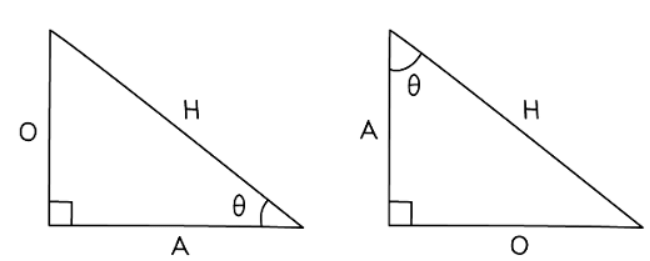
• Note that θ is the Greek letter theta. In a right-angled triangle, consider:
  • O = opposite side to angle θ
  • A = adjacent side next to angle θ
  • H = hypotenuse - 'H' remains constant, while 'O' and 'A' vary based on the angle being referred to.
• Using those labels, the three SOHCAHTOA equations are:

How can we use SOHCAHTOA to find missing lengths?

• If you know the length of one side of a right-angled triangle and one of the angles, you can use SOHCAHTOA to find the lengths of the other sides.
  • Start by labeling the sides of the triangle with H (hypotenuse), O (opposite), and A (adjacent).
  • Choose the appropriate ratio based on the known values and the value you need to find.
    • For example, if you know the angle and the side opposite it (O), and you need to find the hypotenuse (H), use the sine ratio.
  • Substitute the known values into the chosen ratio.
  • Use your calculator or knowledge of trigonometric exact values to solve for the unknown side.

How can we use SOHCAHTOA to find missing angles?

• If you know two sides of a right-angled triangle, you can utilize SOHCAHTOA to determine the size of one of the angles.
• The missing angles can be found using inverse trigonometric functions:

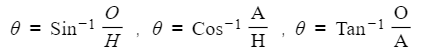
• After selecting the appropriate ratio and substituting the values, apply inverse trigonometric functions either using a calculator or trigonometric exact values to obtain the correct angle measurement.

Do sin, cos and tan work with obtuse angles?

• Your calculator or knowledge of trigonometric exact values can assist in finding sine, cosine, and tangent of any angle. 
• Certain patterns can be helpful, particularly when determining obtuse angles: 
• sin(x) = sin(180° - x)
  • For example, sin(150°) = sin(180° - 150°) = sin(30°)
• cos(x) = -cos(180 - x)
  • For example, cos(150°) = -cos(180° - 150°) = -cos(30°)
• tan(x) = -tan(180 - x)
  • For example, tan(150°) = -tan(180° - 150°) = -tan(30°)
• Exercise caution when dealing with obtuse angles; calculators typically provide the acute angle, so apply the rules above to obtain the correct obtuse angle.

How do I find the shortest distance from a point to a line?

• The most direct route from any point to a line is always the perpendicular distance.
• Construct a right-angled triangle with the point, the perpendicular distance, and a point on the line, then utilize SOHCAHTOA to calculate the distance effectively.