Class 9 Math: Sample Question Paper- 2 (With Solutions) PDF Download
SECTION - A
Questions 1 to 20 carry 1 mark each.
Q.1. If x = 2 + √3, then value of 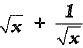 is:
is:
(a) 2 (b) 4 (c) √6 (d) √2
Ans. (c) √6
[∴ x = 2 + √3
⇒ 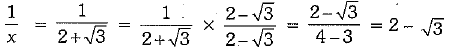
∴ 
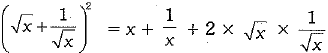
= 4 + 2 = 6
⇒ 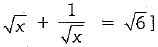
Q.2. If n(A) = 17, n(B) = 8 for two disjoint sets A and B, then n(A ∪ B) =
(a) 9
(b) 23
(c) 25
(d) None of these
Ans. Choice (c) is correct.
As A and B are disjoint sets.
∴ n(A ∪ B) = n(A) + n(B) =17 + 8 = 25
Q.3. The point of intersection of the coordinate axis is
(a) ordinate
(b) abscissa
(c) quadrant
(d) origin
Ans. (d) Origin is the point of intersection of both coordinate axes.
Q.4. The graph of the linear equation 2x + 3y = 6 cuts the y-axis at the point
(a) (2, 0)
(b) (0, 3)
(c) (3, 0)
(d) (0, 2)
Ans. (d) Since the graph of linear equation 2x + 3y = 6 cuts the y -axis. So we put x = 0 in given equation, we get
2x + 3y = 6
2(0) + 3y = 6
0 + 3y = 6
y = 2
Hence, at the point (0, 2) the given linear equation cuts the y-axis.
Q.5. In the figure, AOB is a straight line. The measure of ∠COD is equal to:
(a) 60°
(b) 80°
(c) 120°
(d) 160°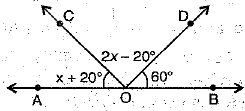
Ans. (a) 600
∴ ∠AOC + ∠COD + ∠BOD = 180°
⇒ x + 20° + 2x - 20° + 60° = 180°
⇒ 3x + 60° = 180°
⇒ 3x = 120°
⇒ 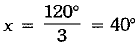
Now, ∠COD = 2x - 20° = 2 x 40° - 20° = 60°]
Q.6. The coefficient of x50 in (1 + x)100 is
(a) 100C50 x50
(b) 100C50
(c) x50
(d) nC50
Ans. Choice (b) is correct.
We know that (r + 1) term in the binomial expansion of (1 + x)n is given by
Tr + 1 = nCr (1)n- r xr = nCr xr
∴ In the binomial expansion of (1 + x)100 is given by
For coefficient of x50, put r = 50 in above, we have
T50 + 1 = 100C50 x50
∴ The coefficient of x50 = 100C50
Q.7. If equation of X-axis is y = k, then the value of k is
(a) 0 (b) 1 (c) 2 (d) 3
Ans.(a) Equation of X-axis is y = 0
∴ k = o
Q.8. An isosceles right triangle has area 8 cm2. The length of its hypotenuse is
(a) √32 cm
(b) √16 cm
(c) √48 cm
(d) √21 cm
Ans. (a)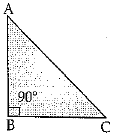
Area of isosceles Δ = 1/2 x Base x height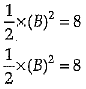
B = √16
= 4 cm
By using Pythagoras theorem
(B)2 + (P)2 = (H)2
(H)2 = (4)2 + (4)2
H = √32 cm
Q.9. Three solid cubes of side 4 cm each are joined to form a cuboid. Then its surface area is:
(a) 288 cm2 (b) 200 cm2 (c) 192 cm2 (d) 224 cm2
Ans. (a) 224 cm2
[∵ Dimensions of the cuboid formed by joining the cubes of side 4 cm are length (l) = 12 cm, breadth (b) = 4 cm and height (h) = 4 cm
∵ Surface area of the cuboid = 2 (lb + bh + hl)
= 2(12 x 4 + 4 x 4 + 4 x 12)
= 2(48 + 16 + 48) = 2 x 112 = 224 cm2]
Q.10. A card is drawn from a well shuffled deck of 52 cards. The probability that the card drawn is an ace of heart is
(a) 1/52
(b) 13/52
(c) 4/52
(d) 1/6
Ans. (a)
One card can be drawn in 52C1 = 52 ways. So, the sample space has 52 equally likely sample points. Let E1 be the event ‘an ace of heart’.
⇒ E1 contains only one sample point.
∴ 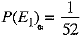
Questions 11 to 15 carry one mark each
Q.11. A polynomial of degree one is called..........
Ans. A polynomial of degree one is known as linear polynomial.
Q.12. Write an example of a constant polynomial.
OR
Factorise 8x3- 64
Ans. Any non-zero real number (eg : p(x) = 7 or p(x) = -5 etc.)
OR
8x3 - 64 = 8(x3 - 8)
= 8(x - 2)(x2 + 2x + 4)
Q.13. Each of the angles of a square is a ........... and each of the four sides are .........
Ans. right angle, equal
Q.14. Coefficient of variation 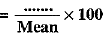
Ans. S.D. (Standard Deviation)
Coefficient of variation = 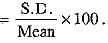
Q.15. The mid value of a class is called...........
OR
A frequency distribution in which each upper limit as well as lower limit are included, is called......
Ans. The mic value of a class is called the class mark.
OR
inclusive form.
Directions (Q. Nos. 16-20) Answer the following questions.
Q.16. The volume of the largest right circular cone that can be fitted in a cube whose edge is 2r equals to the volume of a hemisphere of radius r.
Ans. True
Volume of cone 
= volume of hemisphere
Q.17. Factorise: y2 - 8y + 16.
Ans. We have y2 - 8y + 16
= y2 - 2(y) (4) + 42 [using identity a2 - 2ab+ b2= (a - b)2]
= (y - 4)2 = (y - 4) (y - 4)
Q.18. Find the component statement for the compound statement: Number 7 is prime and odd.
Ans. The component statements are (i) Number 7 is a prime and (ii) Number 7 is an odd.
Q.19. If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar (ΔABC): ar (ΔBDE).
Ans. Let AB = x cm
∴ 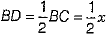

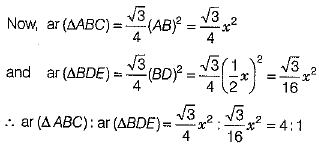
Q.20. The things which are double of the same thing are equal to one another.
Ans. True, Since, it is one of the Euclid's axioms.
SECTION - B
Question numbers 21 to 26 carry 2 marks each.
Q.21. Simplify: 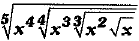
Ans. 
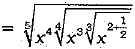
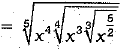
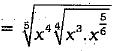



Q.22. In the expansion of  which term is independent of x?
which term is independent of x?
OR
If the different permutation of all the letters of the word EXAMINATION are listed as in a dictionary, how many words are there in this list before the first word starting with E?
Ans. In the expansion of (x + a)n, (r + l)th term is given by Tr + 1 = nCr xn - r ar
∴ In the expansion of 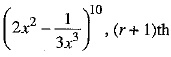 term is given by
term is given by

⇒ 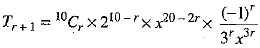
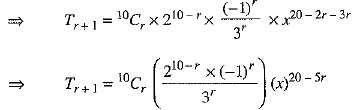
Suppose Tr + 1 is independent of x.
∴ 20 - 5r = 0 ⇒ 5r = 20 ⇒ r = 4
∴ (r + 1)th = (4 + 1)th i.e., 5th term is the required term independent of x.
OR
Total number of letters in the word EXAMINATION are 11.
Starting with A we have to find the number of arrangements of the remaining 10 letters, E, X, M, I, N, A, T, I, O, N, out of which there are 2I’s, 2N’s and the rest are all different.
The number of such arrangements

Clearly, we will have to start the next word with E (as in the dictionary)
So, the required numbers of words in the list before the first word starting with E are 907200.
Q.23. ABCD is a parallelogram and X is the mid-point of AB. If ar (ΔADC) = 24 cm2, then find ar (AXCD).
Ans. Given, ABCD is a parallelogram and X is the mid-point of AS. Draw the diagonal AC.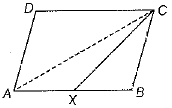
We know that diagonal of a parallelogram divides it into two triangles of equal areas.
So. ar (parallelogram AECD) = 2 x ar (ΔADC)
= 2 x 24 = 48 cm2
Since, CX is the median of ΔABC.
We know that a median of a triangle divides it into two triangles of equal areas.
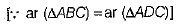
Now, ar(AXCD) = ar(parallelogram ABCD) - ar (ΔBCX)
= 48 - 12 = 36 cm2
Q.24. If (3x -15°) and (x + 5°) are complementary angles, find the angles.
Ans. (3x -15°) + (x + 5°) = 90°
or 4x = 90° + 10° = 100°
or 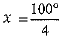
or, x = 25°
Angles are 60° and 30°.
Q.25. The mean of first 8 observations is 18 and last 8 observations is 20. If the mean of all 15 observations is 19, find the 8th observation.
OR
Ten observations 6, 14, 15, 17, x + 1, 2x - 13, 30, 32, 34, 43 are written in an ascending order. The median of the data is 24. Find the value of x.
Ans. Sum of first 8 observations = 8 x 18 = 144
Sum of last 8 observations = 8 x 20 = 160
Sum of 15 observations = 15 x 19 = 285
Thus, 8th observation ~ 144 + 160 = 285 = 304 - 285 = 19
Hence, 8th observation is 19.
OR
Given data is in ascending order and n = 10 (even number)
∴ Median = Average of 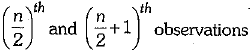
= Average of 5th and 6th term = 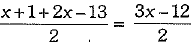
Also, median = 24
∴ 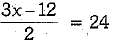
⇒ 3x - 12 = 48
⇒ 3x = 60
⇒ x = 20
Q.26. If P(a, b) is the mid-point of a line segment between axes. Show that equation of the line is 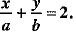
OR
Show that the points (4,7,8), (2,3,4), (-1, - 2,1) and (1,2,5), taken in order form a parallelogram.
Ans. Let the equation of the line AB which cuts the x-axis at A and y-axis at B be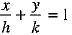 ...(i)
...(i)
If the line (1) cuts the x-axis, then by putting y = 0 in (1), we have x = h
∴ The coordinates of the point A are (h, 0).
Similarly, the line (1) cuts the y-axis, then by putting x = 0 in (1), we have y = k
∴ The coordinates of the point B are (0, k).
If P(a, b) is the mid-point of AB, then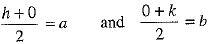

⇒ h = 2a and k = 2b
Substituting the values of h and k in (1), we get the required equation of the line AB is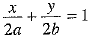
⇒ 
OR
Let the given points A(4, 7, 8), B(2, 3, 4), C (- 1 , - 2 , 1) and D{ 1, 2, 5) be vertices of a quadrilateral.
The coordinates of the mid-point of diagonal AC are 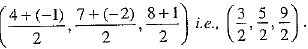
The coordinates of the mid-point of diagonal BD are 
Since, the mid-points of the diagonals AC and BD are same, so the diagonals bisect each other. We know that if the diagonals of a quadrilateral bisect each other, then it is a parallelogram. Hence, ABCD is a parallelogram.
SECTION - C
Question 27 to 34 carry 3 marks each.
Q.27. Observe the graph of the equation f(x) in two variables. Based on graph, answer the following questions:
(i) Name the type of graph.
(ii) Write the coordinates of A, B and C.
(iii) Name the triangle formed by the line and coordinate axes. Also, name of the type of triangle.
Ans. (i) It is a linear graph i.e., it is a line.
(ii) Coordinates of A, B and C are A(4, 0), B (0, 3) and C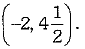
(iii) ΔAOB, since ∠AOB = 90°.
∴ It is a right-angled triangle.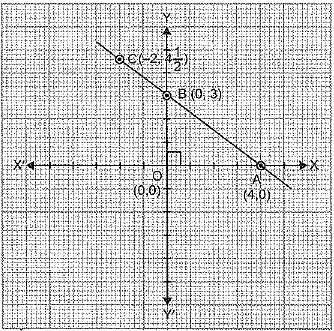
Q.28. A boy has 3 library tickets and 8 books of his interest in the library. Of these 8 books, he does not want to borrow Chemistry Part II unless Chemistry Part I is also borrowed. In how many ways can he choose the three books to be borrowed?
Ans. We have the following two cases:
Case 1: When Chemistry Part I is borrowed:
In this case the boy may borrow Chemistry Part II. So, he has to select now two books out of the remaining 7 books of his interest This can be done in 7C2 ways,
Case 2: When Chemistry Part I is not borrowed:
In this case the boy does not want to borrow Chemistry Part II. So, he has to select three books from the remaining 6 books. This can be done in 6C3 ways.
Hence the required number of ways
Q.29. In the given figure, ABC is an isosceles triangle with AB = AC. BD and CE are two medians of the triangle Prove that BD = CE.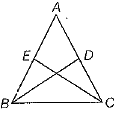
Ans. Given ABC is an isosceles triangle with AB = AC.
BD and CE are two medians.
To prove BD = CE ...(i)
...(i)
[∵ angles opposite to equal sides are equal] ...(ii) [dividing by 2 both sides]
...(ii) [dividing by 2 both sides]
Thus, in ΔDCB and ΔEBC, we get
DC = EB [from Eq. (ii)]
CB = BC [common side]
and ∠DCB = ∠EBC [from Eq. (i)]
Q.30. Find the area of triangular region ABC having two sides are 18 m and 10 m and the perimeter is 42 m.
OR
Sides of a triangle ABC are in the ratio 12 :17:25 and its perimeter is 540 cm. Find its area.
Ans. 42 = 18 + 10 + c
c = 42 - 28 = 14 m
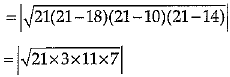
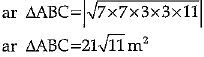
OR
Given: sides of triangle are in the ratio 12:17:25
∴ Sides are 12x, 17x and 25x respectively.
Perimeter = 540 cm
12x + 17x + 25x =540
54x = 540
x = 10
Now 
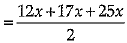
s = 27x = 27 x 10 = 270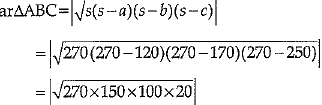
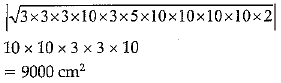
Q.31. In the given figure, find x.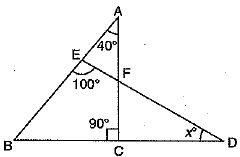
OR
In the given fig., lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.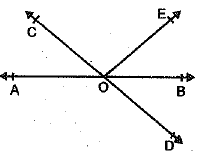
Ans. In ΔABC, we have
∠A + ∠B +∠C = 1800
⇒ 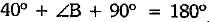
⇒ ∠B = 1800 - 1300
⇒ ∠B = 500
Now, in ΔBDE, we have
⇒ 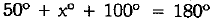
⇒ 
⇒ 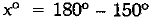
⇒ x0 = 300
⇒ x = 30
Or
∠AOC and ∠BOD are vertically opposite angles.
∴ ∠AOC = ∠BOD
⇒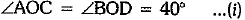 [given]
[given]
Now, 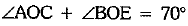 [given]
[given]
⇒ 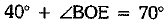 [using (i)]
[using (i)]
⇒ 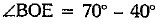
⇒ 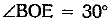
Also, 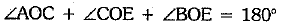 [linear pair axiom]
[linear pair axiom]
⇒ 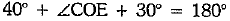
⇒ 
⇒ 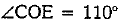
Now, ∠COE + reflex ∠COE = 360° [angles at a point]
⇒ 1100 + reflex ∠COE = 360°
⇒ reflex ∠COE = 360° - 110°
⇒ reflex ∠COE = 250°
Q.32. Let A = (1, 2, 3, ...., 20). Define a relation R from A to A by R = {(a, b) : a - 2b = 0, a, b ∈ A}. Depict the relation using roster form. Write domain and range of the relation.
Ans. Given, A = {1, 2, 3 , ....... ,20} and R = {(a, b): a - 2b = 0; a, b ∈ A}
For a, b ∈ A, a - 2b = 0 ⇒ a/2


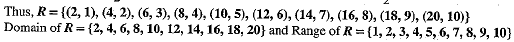
Q.33. The mean of 50 items was found to be 40. If at the time of calculation two items were wrongly taken as 32 and 12 instead of 23 and 11. then find the correct mean.
Ans.
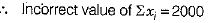 ...(i)
...(i)
Now, correct value of ∑xi = Incorrect value of ∑xi - (Sum of incorrect value + (Sum of correct values)
⇒ Correct value of ∑xi = 2000 - (32 + 12) + (23 + 11) = 1990 (1)
= 1990/50 = 39.8
Q.34. 1500 families with 2 children were selected randomly, and following data were recorded.
| Number of girls | 2 | 1 | 0 |
| Number of families | 475 | 814 | 211 |
Find the probability that a family chosen at random, having
(i) 2 girls (ii) 1 girl (iii) no girl
Ans.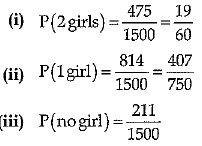
SECTION - D
Questions 35 to 40 carry 4 marks each
Q.35. If 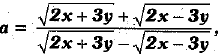 find the value of 3ya2 - 4xa + 3y.
find the value of 3ya2 - 4xa + 3y.
Ans. 
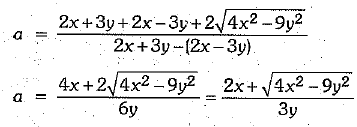
 ⇒
⇒ 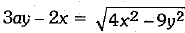 ...(i)
...(i)
Squaring both sides of eqn. (i), we have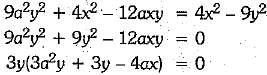
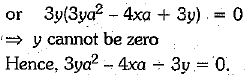
Q.36. Find domain and range of the real function f(x) = 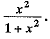
Ans. The given function is f(x)= 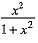
∴ Function 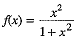 is defined for all real values of x as 1 + x2 ≠ 0 for all x ∈ R.
is defined for all real values of x as 1 + x2 ≠ 0 for all x ∈ R.
Hence, domain of the function is R.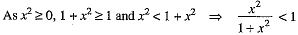
∴ 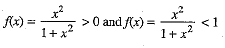
⇒ 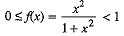
∴ Range of f(x) = [0,1)
Q.37. Three coins are tossed simultaneously 180 times and it is found that 3 tails appeared 34 times, 2 tails appeared 55 times, 1 tail appeared 72 times and no tail appeared 19 times. Find the probability of getting (i) 3 tails (ii) 2 tails (iii) l tail (iv) 0 tail.
OR
On a busy road, following data was observed about cars passing through it and number of occupants
Find the chance that it has
(i) exactly 5 occupants (ii) more than 2 occupants (iii) less than 5 occupants (iv) greater than 5 occupants
Ans. Given, total number of trials =180
Number of times 3 tails appeared = 34
Number of times 2 tails appeared = 55
Number of times 1 tail appeared = 72
Number of times 0 tail appeared =19
(i) P (getting 3 tails)
(ii) P (getting 2 tails)

OR
Total number of cars = 100
∴ The total numbers of trials = 100
(i) The numbers of trial, exactly 5 occupants = 5
∴ P(exactly 5 occupants) = 5/100 = 1/20
(ii) The numbers of trial, more than 2 occupants
= 23+17+5 = 45
∴ P(more than 2 occupants) = 45/100 = 9/20
(iii) The numbers of trial, less than 5 occupants
= 29+26+23+17 = 95
∴ P(less than 5 occupants) = 95/100 = 19/20
(iv) The number of trials, greater than 5 occupants = 0
∴ P (greater than 5 occupants) = 0/100 = 0
Q.38. Evaluate the following using suitable identities.
(a) (102)3 (b) 104 x 96
OR
Find the value of 'a' if remainder is same when polynomial p(x) = x3 + 8x2 + 17x + ax is divided by (x + 2) and (x + 1).
Ans.(a) (102)3 = (100 + 2)3
[∵ (a + b)3 = a3 + b3 + 3ab(a + b)]
(100 + 2)3 = (100)3 + (2)3 + 3 x 100 x 2(100+ 2)
1023 =10,00,000 + 8 + 600(102)
= 10,00,000 + 8 + 61200
1023 = 1061208
(b) 104 x 96 = (100+4)(100-4)
= (100)2 - (4)2
[a2 - b2 =(a + b)(a-b)]
104 x 96 = 10000 - 16 = 9984
OR
p(x) = x3 + 8x2 + 17x + ax
p(x) leave the same remainder when divided by (x + 2) and (x + 1).
Q.39. If each diagonal of a quadrilateral divides it into two triangles of equal areas, then prove that quadrilateral is a parallelogram.
OR
Diagonals PR and QS of quadrilateral PQRS intersect at T, such that PT = TR. If PS = QR, show that: ar(ΔPTS) = ar(ΔRTQ).
Ans. Given: A quad ABCD such that diagonals AC and BD divides it into two triangles of equal areas
i.e., ar(ΔABD) = ar(ΔCDB)
and ar(ΔABC) = ar(ΔACD)
To Prove: ABCD is a parallelogram
Proof: Diagonal AC divides the quad. ABCD into two triangles of equal area
∴ ar(ΔABC) = ar(ΔACD) ...(i)
Also, ar(ΔABC) + ar(ΔACD) = ar(quad. ABCD)
⇒ ar(ΔABC) + ar(ΔABC) = ar(quad. ABCD) [using (i)]
⇒ 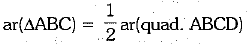 ...(ii)
...(ii)
Again, diagonal BD of the quad. ABCD divides it into two triangles of equal area
∴ ar(ΔABD) = ar(ΔBCD) (iii)
Also, ar(ΔABD) + ar(ΔBCD) = ar(quad. ABCD)
⇒ ar(ΔABD) + ar(ΔABD) = ar(quad. ABCD) [using (iii)]
⇒ 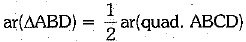 ...(iv)
...(iv)
From (ii) and (iv), we obtain
ar(ΔABC) = ar(ΔABD)
OR
Given : In quad. PQRS, diagonals PR and QS intersect at T.
To prove: ar(ΔPTS) = ar(ΔRTQ)
Construction: From P and R, draw perpendiculars PE ⊥ SQ and RF ⊥ SQ.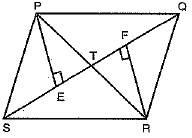
Proof: In ΔPET and ΔRTF,
TP = TR [given]
∠PTE = ∠RTF [vert. opp. angles]
∠PET = ∠RFT = 900 [construction]
ΔPET ≅ ΔRFT [AAS congruency]
⇒ ar(ΔPET) = ar(ΔRFT)...(i) [congruent figures have equal area]
and PE = RF [c.p.c.t.]
Now, in ΔPSE and ΔRQF,
∠PES = ∠RFQ [right angle]
PE = RF [proved above]
PS = QR [given]
So, ΔPSE ≌ ΔRQF [RHS congruency]
⇒ ar(ΔAPSE) = ar(ΔRQF) ...(ii)
Adding (i) and (ii), we have
ar(ΔPET) + ar(ΔPSE) = ar(ΔRFT) + ar(ΔRQF)
⇒ ar(ΔPTS) = ar(ΔRTQ)
Q.40. In the expansion of 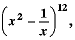 find (i) middle term and (ii) term independent of x.
find (i) middle term and (ii) term independent of x.
Ans. Let Tr + 1 denote the (r + 1) the term in the expansion of  then
then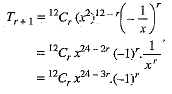
(i) As the number of terms in the expansion of 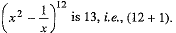
Since 13 is an odd number, then there is only one middle term viz., 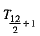 term, i.e., T7 term.
term, i.e., T7 term.
Now, 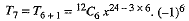 [Putting r= 6 in (1)]
[Putting r= 6 in (1)]
(ii) Let Tr + 1 be the term independent of x in the expansion 
Then, 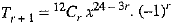
The term will be independent of x, if the power of x is zero, i.e., 24 - 3r = 0 ⇒ r = 8
Substituting r = 8 in (1), we get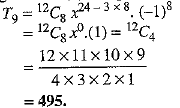
FAQs on Class 9 Math: Sample Question Paper- 2 (With Solutions)
| 1. What is the format of Class 9 Math Sample Question Paper- 2? |  |
| 2. How can I access the solutions for Class 9 Math Sample Question Paper- 2? |  |
| 3. Are the questions in Class 9 Math Sample Question Paper- 2 similar to the ones in the actual exam? |  |
| 4. Can I use Class 9 Math Sample Question Paper- 2 as a study resource? |  |
| 5. How can I effectively utilize the solutions provided for Class 9 Math Sample Question Paper- 2? |  |


















