Class 9 Math: Sample Question Paper- 3 (With Solutions) PDF Download
SECTION - A
Questions 1 to 20 carry 1 mark each.
Q.1. 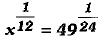 then x is equal to:
then x is equal to:
(a) 49
(b) 2
(c) 12
(d) 7
Ans: (d)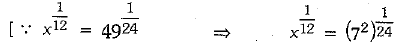
⇒ 
Q.2. Given n(U) = 20, n(A) = 12, n(B) = 9, n(A ∩ B) = 4, where U is the universal set, then [n(A ∪ B)C] is equal to
(a) 3
(b) 9
(c) 11
(d) 16
Ans: Choice (a) is correct.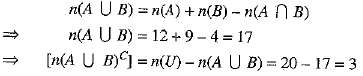
Q.3. The abscissa and ordinate of the origin are
(a) (0,0)
(b) (1,0)
(c) (0,1)
(d) (1,1)
Ans: (a) The abscissa and ordinate of the origin are (0,0)
Q.4. The equation 2x + 5y = 7 has a unique solution, if x, y are :
(a) Natural numbers
(b) Positive real numbers
(c) Real numbers
(d) Rational numbers
Ans: Correct option : (a)
Explanation: In natural no., there is only one pair, i.e., (1/1) which satisfy the given equation.
But in positive real no, and rational no., there are many pairs which satisfy the given linear equations.
Q.5. If AB ║ EF and EF ║ CD, value 0f x is given by :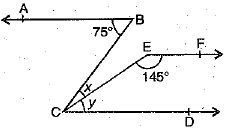
(a) 35°
(b) 45°
(c) 40°
(d) 60°
Ans: (c) 40°
[∵ y + 145° = 180°
Q.6. The intercepts cut by the line 3x + 5y = 15 on the x-axis and the y-axis are
(a) 8 and 3
(b) 5 and 3
(c) 3 and 3
(d) 5 and 5
Ans: Choice (b) is correct.
Putting y = 0 in the equation, we get 3x = 15 i.e., x = 5 ⇒ Intercept on x-axis = 5
Putting x = 0 in the equation, we get 5y = 15 i.e., y = 3 ⇒ Intercept on y-axis = 3
Q.7. If x = 2 k- 1 and y = k is a solution of the equation 3x - 5y - 7 =0, find the value of k.
(a) 2
(b) 5
(c) 10
(d) 15
Ans: (c) It is given that x = 2k - 1 and y = k is a solution of the given equation.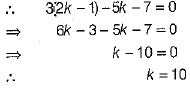
Q.8. In the given figure, if ∠OAB = 40°, then ∠ACB is equal to: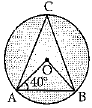
(a) 50°
(b) 40°
(c) 60°
(d) 70°
Ans: Correct option : (a)
Explanation :
In ΔOAB
OA = OB [Radii of circle]
∠OBA = ∠OAB
[Angles opposite to equal sides of a triangle are equal.]
Therefore,
∠AOB=180° - (40°+40°) = 100°
Since the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.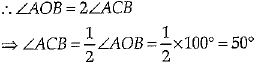
Q.9. If areas of three adjacent faces of a cuboid be x, y and z respectively then its volume is
(a) 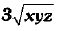
(b) 2xyz
(c) xyz
(d) 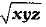
Ans: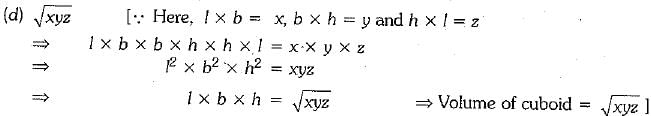
Q.10. The fourth term from the end of the G.P. 8, 4, 2, ...... is
(a) 1/16
(b) 1/4
(c) 1/8
(d) 1/32
Ans: Choice (a) is correct,
The series is a G.P. with a 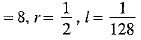
The nth term ln from end is given by ln = 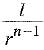
The fourth term ln from end is given by l4 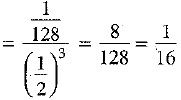
Directions (Q. Nos. 11-15) Fill in the blanks
Q.11. A polynomial of degree two is called_________.
Or
A biquadratic polynomial is of degree__________.
Ans: A polynomial of degree two is called quadratic polynomial.
Or
A bi-quadratic polynomial is of degree 4 (four).
Q.12. The sum of interior angles of a parallelogram is 360°
OR
The diagonals of a parallelogram bisect each other
Ans: True
OR
True
Q.13. Two congruent figures have_________areas but the converse need not be true.
Ans: equal
Q.14. The number of terms in the expansion of (a + b + c)4 is_________.
Ans: 15
We know that the number of terms in the expansion of (a + b + c)n is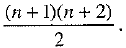
∴ Number of terms in the expansion of (a + b + c)4 = 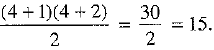
Q.15. In a histogram, the class intervals or the groups are taken along_______.
Ans: In a histogram, the class intervals or the groups are taken along X-axis.
Q.16. Find the value of a, if x - a is a factor of x3 - ax2 + 2x + a - 1.
Ans: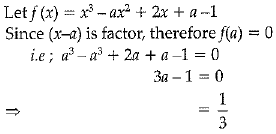
Q.17. Find the zeroes of the polynomial p(x) - (x - 2)2 - (x + 2)2.
Ans: Put p(x) = 0
⇒ (x - 2)2 - (x + 2)2 = 0
⇒ (x - 2 + x + 2) (x - 2 - x - 2) = 0
⇒ 2x (- 4) = 0
⇒ - 8x = 0
Thus, x = 0, is a zero of the polynomial p(x).
Q.18. If (1 + i)z = (1 - i)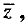 prove that
prove that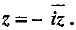
Or
Solve : ix2 + 2x - i = 0
Ans: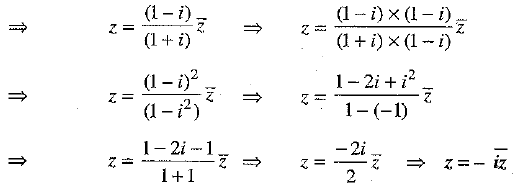
Or
ix2 + 2 x - i = 0
Here, a = i , b = 2 , c = - i [Comparing the equation with ax2 + bx + c = 0]
We know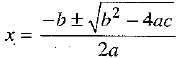
∴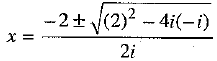
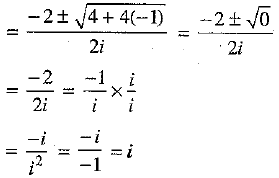
Q.19. In the given figure, find the values of x and y.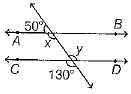
Ans: Since, x and 50° form a linear pair.
x + 50° = 180°
⇒ x = 130°
Since, vertically opposite angles are equal.
∴ y = 130°
Q.20. Find the area of triangle whose sides are 4 cm, 5cm and 3cm.
Ans: Now, 32 + 42 = 52 ⇒ 9 + 16 = 25 ⇒ 25 = 25
∴ The given triangle is right angled.
[∵ Pythagoras theorem is applicable is Δ]
Area of triangle = 1/2 bh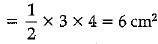
SECTION - B
Question numbers 21 to 26 carry 2 marks each.
Q.21. Sudhir and Ashok participated in a long jump competition along a straight line marked as a number line. Both start the jumps one by one but in Opposite directions. From ‘O’ Ashok jumps one unit towards the positive side while Sudhir jumps double in units as Ashok jumps, along negative side. After jumping 4 jumps each, at which point Ashok and Sudhir reached. What is the distance between their final positions? Ashok argues that he is the winner since Sudhir is at negative side. Who do you think is winner and why?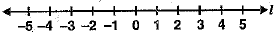
Ans: After jumping four jumps each, Ashok reached at 4 in positive direction and Sudhir reached at - 8 i.e., in negation direction. Distance between their final positions is 12 units. Here, distance covered by Sudhir is 8 units and distance covered by Ashok is 4 units. Thus, Sudhir is the winner.
Q.22. Prove that: tan 9A - tan 6A - tan 3A = tan 9A.tan 6A.tan 3A.
Ans: We know that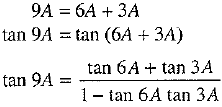
Q.23. Government of India is working regularly for the growth of handicapped persons. For this, three STD booths situated at A, B and C as shown in the figure, which are operated by handicapped persons. These three booths are equidistant from each other as shown in the figure.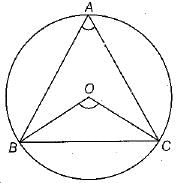
(i) Find ∠BAC.
(ii) Find ∠BOC.
Ans: (i) Here, A, B and C represented three STD booths.
As, A, B, C are equidistant from each other
AB = BC =CA
Then, ΔABC is an equilateral triangle.
Hence, ∠BAC = ∠ABC =∠BCA = 60°
(ii) We know that the angle substended by an arc at the centre of the circle is twice the angle subtended by it at any point on the remaining part of the circle.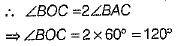
Q.24.In a triangle PQR, X and Y are the points on PQ and QR respectively. If PQ = QR and QX = QY, show that PX = RY.
Ans: Here PQ = QR
and QX = QY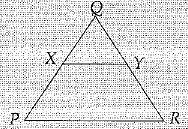
If equals are subtracted from equals, the remainders are also equal
We have PQ - QX = QR - QY
PX = RY
Q.25. Ten observations 6, 14, 15, 17, x + 1, 2x - 13, 30, 32, 34, 43 are written in an ascending order. The median of the data is 24. Find the value of x.
Or
A class consists of 50 students out of which 30 are girls. The mean of marks scored by girls in a test is 73 (out of 100) and that of boys is 71. Determine the mean score of the whole class.
Ans: Given data is in ascending order and n = 10 (even number)
∴ 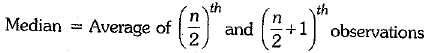
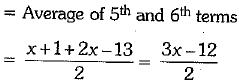
Also, median = 24
∴ 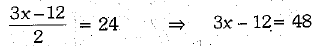
⇒ 3x = 60 ⇒ x = 20
Or
Here, number of girls = 30
∴ Number of boys = 50 - 30 = 20
Mean of marks by girls = 73
Mean of marks by boys = 71
Thus, combined mean = 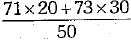
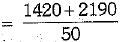
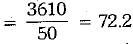
Q.26. Find the coefficient of x3 in the expansion of (1 + x + x2)3
OR
Find (a + b)4 - (a - b)4. Hence evaluate: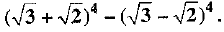
Ans: Let y = x + x2
(1 + x + x2)3 = (1 + y)3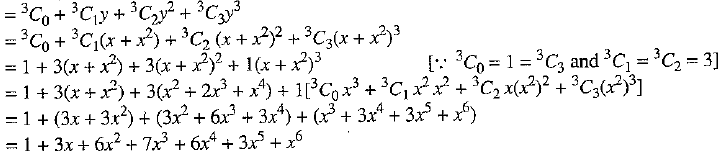
∴ Coefficient of x3 = 7.
OR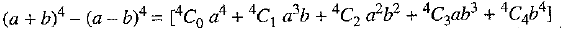
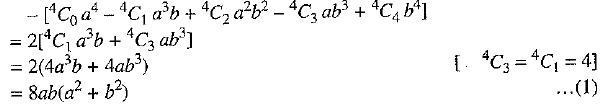
Putting a = √3 and b = √2 in (1), we get
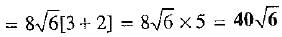
SECTION - C
Question 27 to 34 carry 3 marks each.
Q.27. Planting more and more trees is helpful in reducing pollution and make the environment clean and green for our coming generations. Keeping in mind above, on environment day, class-9 students got five plants of mango, silver oak, orange, banyan and amla from soil department. Students planted the plants and noted their locations as (x, y).
Plot the points (x, y) in the graph and join them in the given order. Name the figure you get.
Ans: The given trees (points) are Mango (2, 0), Silver Oak (3, 4), Orange (0, 7), Banyan (- 3. 4) and Amla (-2, 0). The location of these trees are shown in the graph.
On joining the points of mango, silver oak, orange, banyan and amla in order the figure so formed is a regular pentagon.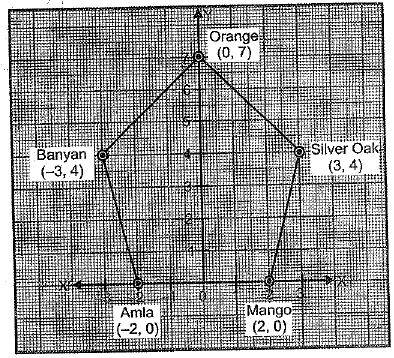
Q.28. If a + ib =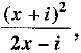 prove that a2 + b2
prove that a2 + b2 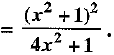
OR
Find the square root of 4 - 4√3i.
Ans: Given: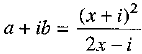 ...(1)
...(1)
We know that if two complex numbers are equal, then their conjugates are also equal. Taking conjugate of both sides, we get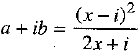 ...(2)
...(2)
Multiplying corresponding sides of both equations (1) and (2), we get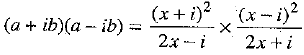
⇒ 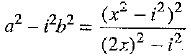
⇒ 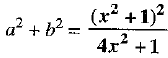

OR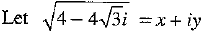 ...(1)
...(1)
Squaring both sides, we have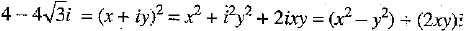
Comparing real and imaginary parts on both sides, we have
x2 - y2 = 4 ...(2)
and 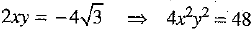 ...(3)
...(3)
Now, 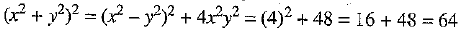 [using (2) and (3)]
[using (2) and (3)]
Taking square root of both sides, we have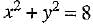 ...(4) [∵ Sum of squares of real numbers cannot be negative]
...(4) [∵ Sum of squares of real numbers cannot be negative]
Adding and subtracting (2) and (4), we get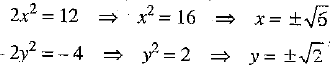
Since xy < 0, therefore x and v are of opposite sign.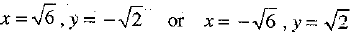
Putting the values of x and y in (1), we get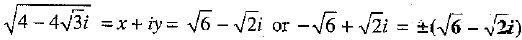
Q.29. A survey of 200 people was conducted about their preference for visiting various pavilions.
Find the probability that selected person visited
(i) both Good living and Delhi pavilion.
(ii) only Defence pavilion.
(iii) both Toy and Defence pavilion.
Or
Probability of getting a blue ball is 2/3 from a bag containing 6 blue and 3 red balls. 12 red balls are added in the bag, then find the probability of getting.
(i) a blue ball.
(ii) a red ball.
Ans: Total number of people = 200
(i) P(Good living and Delhi pavilion)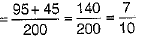
(ii) P(only Defence pavilion) 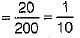
(iii) P(both Toy and Defence pavilion)
Or
Given, number of blue balls in bag = 6
and the number of red balls in bag = 3
Total number of balls in a bag = 6+3=9
After adding 12 red balls,
Total number of balls = 9+12=21
Number of red balls = 3+12 = 15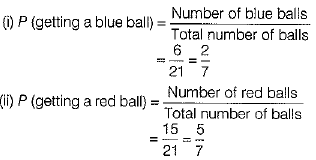
Q.30. In ΔPQR, A and B are points on sides QR such that they trisect QR. Prove that :
ar (ΔPQB)=2ar (ΔPBR)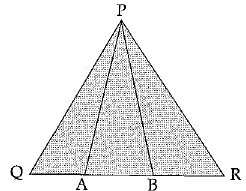
Ans: Given: PQR is a triangle and A and B are points on QR such that QA = AB = BR
To prove that: ar (ΔPQB) = 2ar (ΔPBR)
Let h be the height of triangle PQR.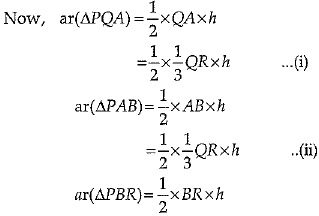

From (i), (ii) and (iii), we conclude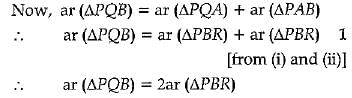
Q.31. In the given figure, a point 0 is taken inside an equilateral quadrilateral PQRS, such that OP = OR. Show that Q, O and S tie on the same straight line.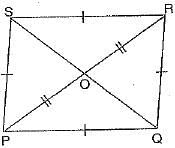
Or
PQRS is a kite in which PQ = PS and QR = SR. Show that PR is the perpendicular bisector of the diagonal QS.
Ans:
Since quadrilateral PQRS is an equilateral
∴ PQ = QR = RS = SP
In ΔPSO and ΔRSO, we have
SP = RS [given]
SO = SO [common]
PO = OR [given]
∴By using SSS congruence rule, we have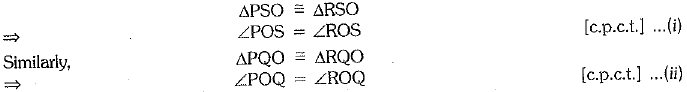
We know that sum of angles at a point is 360°
Hence, Q, O and S lie on a line.
OR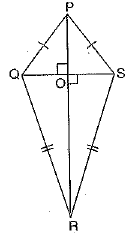
Consider ΔPQR and ΔPSR

Hence, PR is the perpendicular bisector of diagonal QS.
Q.32. Evaluate : 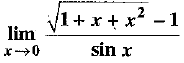
Ans: 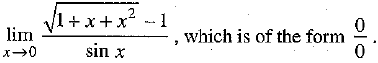
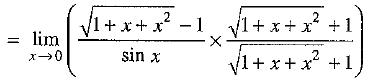 [ Rationalising the numerator]
[ Rationalising the numerator]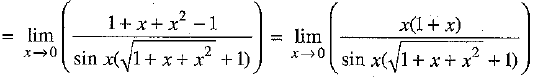
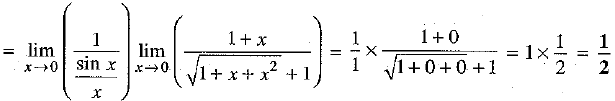
Q.33. If a and b are rational numbers and 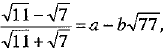 then find the values of a and b.
then find the values of a and b.
Ans: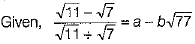
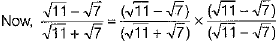 [by rationalisation]
[by rationalisation]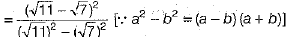
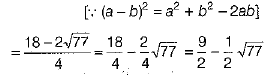
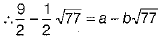
On comparing both sides, we get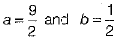
Q.34. The weights of 60 persons in a group are given below :
Find the probability that a person selected at random has :
(i) weight less than 65 kg
(ii) weight between 61 and 64 kg
(iii) weight equal to or more than 64 kg
Ans: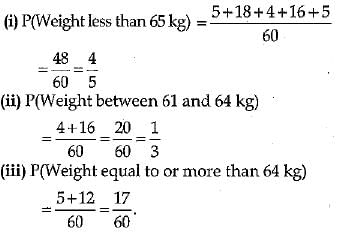
SECTION - D
Questions 35 to 40 carry 4 marks each
Q.35. If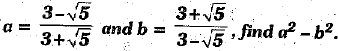
Or
Ans: We have 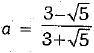
⇒ 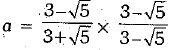
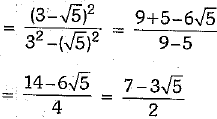
Similarly, we have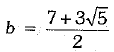
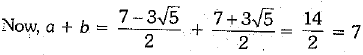
and 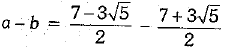
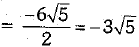
Hence, 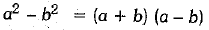
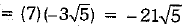
OR
x = √3 - 2
⇒ 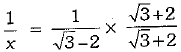
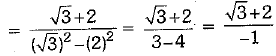
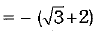
Now,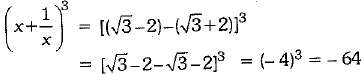
Q.36. Prove that: sin x + sin y + sin z - sin (x + y + z) =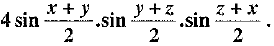
Or
If x cos θ = y cos 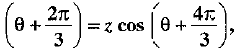 then prove that xy + yz + zx = 0.
then prove that xy + yz + zx = 0.
Ans: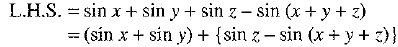
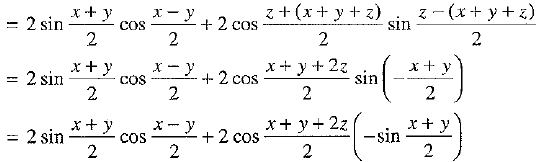
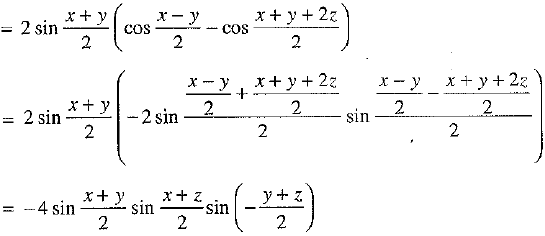
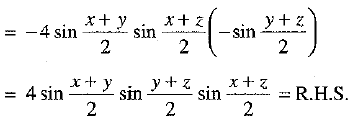
Or
Given: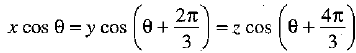
⇒ 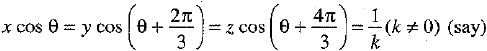
⇒ 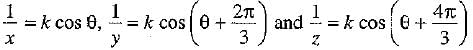 ...(1)
...(1)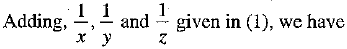
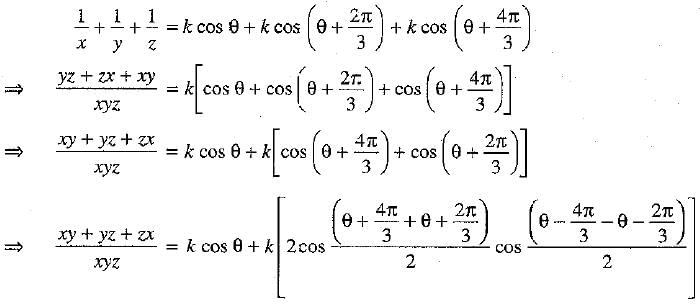
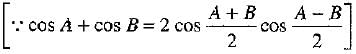
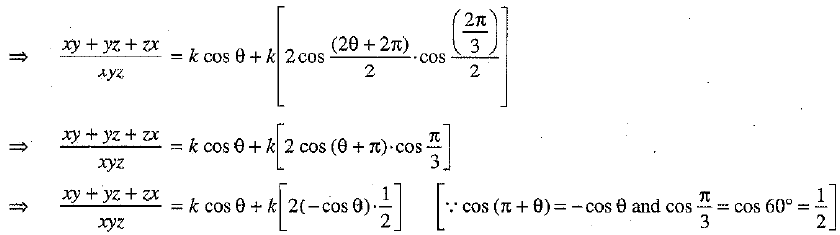

Q.37. If 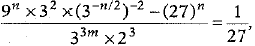 then prove that m - n = 1.
then prove that m - n = 1.
Or
If 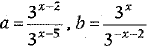 and a - b = 0 , find the value of x.
and a - b = 0 , find the value of x.
Ans: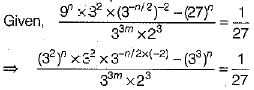
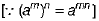
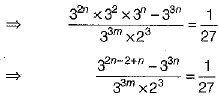
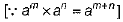
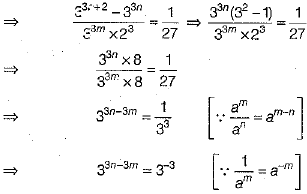
On comparing the powers from both sides, we get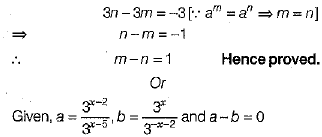

Q.38. Construct a triangle ABC, in which ∠B - 60°, ∠C=45° and AB + BC + CA = 11 cm.
Ans: Steps of construction :
(i) Draw a line segment XY = 11 cm (as AB + BC + CA = 11 cm).
(ii) Construct an angle ∠PXY of 60° at point X and an angle ∠QYX of 45° at point Y.
(iii) Bisect ∠PXY and ∠QYX. These bisectors intersect each other at point A.
(iv) Draw perpendicular bisectors ST of XA and UV of YA.
(v) Perpendicular bisector ST intersects XY at B and UV intersects XY at C. Join AB,AC.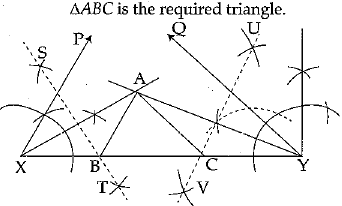
Q.39. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is Rs.12 per m2, what will be the cost of painting all these cones?
Ans: Here, diameter of the base of a cone = 40 cm
∴ Radius of the base of the cone (r)= 20 cm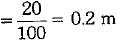
Height of the cone (h) = 1 m
∴ 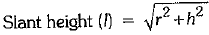
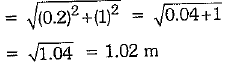
Now, curved surface area of each cone = πrl
= 3.14 x 0.2 x 1.02
= 0.64056 m2
Curved surface area of 50 such cones = 50 x 0.64056 = 32.028 m2
Total cost of painting all these cones at the rate of Rs. 12 per m2 = Rs. 12 x 32.028
= Rs. 384.34
Q.40. Solve the following system of inequations graphically :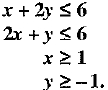
Ans: Converting the inequations into equations, we obtain
x + 2y = 6, 2x + y = 6, x = 1, y = - 1
Region represented by x + 2y < 6
The line x + 2y - 6 meets the coordinate axes at A(6, 0) and 5(0, 3), respectively. Join these points by a hick line. Clearly, (0, 0) satisfies the inequation x + 2y < 6; so the portion containing the origin represents the solution set of the given inequation.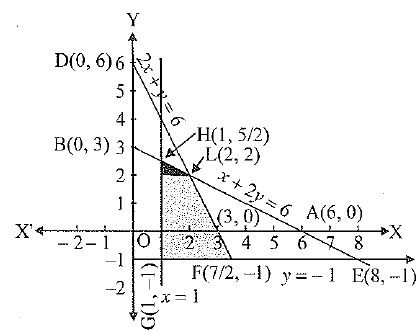
Region represented by 2x + y < 6
The line 2x + y = 6 meets the coordinate axes at C(3, 0) and D(0, 6) respectively. Join these points by a thick line. Clearly, (0, 0) satisfies the inequation 2x + y < 6; so the portion containing the origin represents the solution set of the given inequation.
Region represented by x > 1
Clearly, x = 1 is a line parallel to y-axis at a distance of 1 unit from the origin. Clearly, (0,0) does not satisfies the inequation x > 1; so the portion not containing the origin represents the solution set of the given inequation.
Region represented by y > - 1
Clearly, y = - 1 is a line parallel to v-axis at a distance of 1 unit below the origin. Clearly, (0, 0) satisfies the inequation y > - 1; so the portion containing the origin represents the solution set of the given inequation.
The shaded regions GFLHG represented by the given inequations are shown in figure.
The coordinates of the shaded region GFLH are G(1, - 1), F 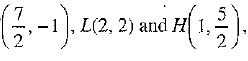 respectively.
respectively.
FAQs on Class 9 Math: Sample Question Paper- 3 (With Solutions)
| 1. What is the format of the Class 9 Math Sample Question Paper-3? |  |
| 2. Are the questions in the Class 9 Math Sample Question Paper-3 similar to the ones in the actual exam? |  |
| 3. How can the Class 9 Math Sample Question Paper-3 help in exam preparation? |  |
| 4. Where can I find the solutions to the Class 9 Math Sample Question Paper-3? |  |
| 5. Can the Class 9 Math Sample Question Paper-3 be used for self-assessment? |  |














