Sample Question Paper- 4 | Mathematics (Maths) Class 8 PDF Download
Class - VIII
Mathematics
Time - 3 hrs
M.M. - 80 Marks
General Instructions :
1. All questions are compulsory.
2. The question paper consist of 30 questions divided into four sections A, B, C and D. Section A comprises of 6 questions of 1 mark each, Section B comprises of 6 questions of 2 marks each, Section C comprises of 10 questions of 3 marks each and Section D comprises of 8 questions of 4 marks each.
3. There is no overall choice. 4. Use of calculator is not allowed.
SECTION ‘A’ (1 mark each)
Q.1. Write the first five square numbers.
Ans. 1, 4, 9, 16, 25
Q.2. Factorise : 12x + 36
Ans. 12x + 36
12x = 2 × 2 × 3 × x
36 = 2 × 2 × 3 × 3
The common factors of the three terms are 2, 2 and 3.
Therefore,
12x + 36 = (2 × 2 × 3 × x) + (2 × 2 × 3 × 3)
= 2 × 2 × 3 (x + 5)
= 12(x + 3)
Q.3. Is 500 a perfect cube ?
Ans. 500 = 5 × 5 × 5 × 2 × 2
∵ In the above prime factorisation 2 × 2 remain after grouping the prime factors in triples.
∴ 500 is not a perfect cube.
Q.4. Factorise :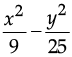
Ans.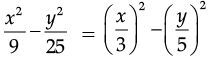
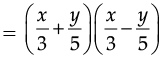
Q.5. Express 3–5 × 3–4 as a power of 3 with positive exponent.
Ans. 3–5 × 3–4 = 3–9 = 
Q.6. If the division N/2 leaves a remainder of 1, what might be the one’s digit of N ?
Ans. N is odd; so its one’s digit is odd. Therefore, the one’s digit must be 1, 3, 5, 7 or 9.
SECTION ‘B’ (2 marks each)
Q.7. Find the volume of the following cuboids figure.
(a)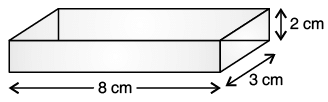
(b)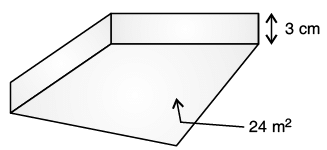
Ans. (a) l = 8 cm, b = 3 cm, h = 2 cm
The volume of cuboid = l × b × h
= 8 × 3 × 2
The volume of cuboid = 48 cm3
(b) Height = 3 cm = 0.03 m
Area of rectangle part = 24 m2
The volume of cuboid = Area of rectangle part × Height
= 24 m2 × 0.03 m
The volume of cuboid = 0.72 m3
Q.8. If 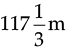 long rope is cut into equal pieces measuring
long rope is cut into equal pieces measuring 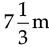 each. How many such small pieces are there ?
each. How many such small pieces are there ?
Ans. Given, Length of rope = 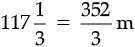
Length of each small piece = 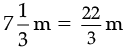
Number of such small pieces = 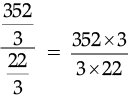
= 16
Q.9. Factorise :
(a) 12x + 36
(b) 22y – 33z
Ans.
(a) We have, 12x = 3 × 2 × 2 × x
= (2 × 2 × 3) × x
36 = 2 × 2 × 3 × 3
= (2 × 2 × 3) × 3
∴ 12x + 36 = [(2 × 2 × 3) × x] + [(2 × 2 × 3) × 3]
= 2 × 2 × 3 [x + 3]
= 12 (x + 3)
(b) We have 22y = 2 × 11 × y
332 = 3 × 11 × 2
22y + 33z = 2 × 11 × y + 3 × 11 × 2
= 11 (2y + 3z)
Q.10. Find the value of x, 10000x = (9982)2 – (18)2
Ans. R.H.S
= (9982)2 – (18)2
= (9982 + 18) (9982 – 18) [Since, a2 – b2 = (a + b) (a – b)]
= (10000) × (9964)
L.H.S = (10000) × x
Comparing L.H.S. and R.H.S, we get
10000x = 10000 × 9964
or x 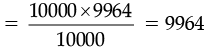
11. A machinery worth Rs. 10,500 depreciated by 5%. Find its value after one year.
Ans. P = Rs. 10,500
Reduction = 5% of Rs. 10,500 per year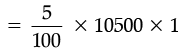
Reduction = Rs. 525
Value after 1 year = 10,500 – 525
Cost value after 1 year = Rs. 9975
Q.12. The length and breadth of a rectangle are 3x2 – 2 and 2x + 5 respectively. Find its area.
Ans. Here, length = 3x2 – 2
breadth = 2x + 5
∴ Area = (length) × (breadth)
= (3x2 – 2) × (2x + 5)
= 3x2 (2x + 5) + (– 2) (2x + 5)
= 6x3 + 15x2 – 4x – 10
Thus, the required area of the rectangle is 6x3 – 15x2 – 4x – 10 sq. units.
SECTION ‘C’ (3 marks each)
Q.13. Simplify :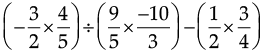
Ans. 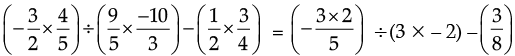
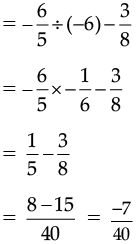
Q.14. Simplify and solve the following :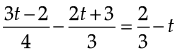
Ans. 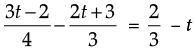
or, 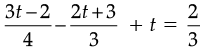
or, 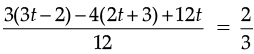
or, 9t – 6 – 8t – 12 + 12t = 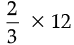
or, 13t – 18 = 8
or, 13t = 8 + 18
or, 13t = 26
or, 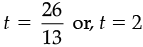
To check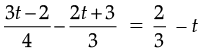
or, 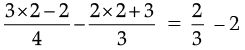
or, 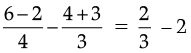
or, 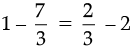
or, 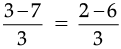
or, 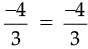
or, LHS = RHS
Q.15. There is a narrow rectangular plot, reserved for a school, in Mahuli village. The length and breadth of the plot are in the ratio 11 : 4. At the rate Rs. 100 per metre it will cost the village panchayat Rs. 75000 to fence the plot. What are the dimensions of the plot ?
Ans. Let the length and breadth of the plot be 11 x and 4x, respectively.
∴ Perimeter of the plot = 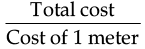
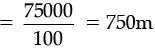
We know that perimeter of rectangle = 2 (l + b)
∴ According to question,
2 (11x + 4x) = 750
or, 15x = 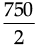
or, 15x = 375
or, x = 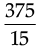
or, x = 25
Hence, length of plot = 11 × 25 = 275 m
and breadth of the plot 4 × 25 =100 m.
Q.16. The denominator of a rational number is greater then its numerator by 8. If the numerator is increased by 17 and the denominator is decreased by 1, the number obtained is 3/2. Find the rational number.
Ans. Let the numerator of rational number be x
and denominator = x + 8
Therefore rational number = 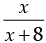
According to question,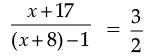
or, 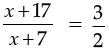
or, 2 (x + 17) = 3 (x + 7)
or, 2x + 34 = 3x + 21
or, 2x – 3x = 21 – 34 [Transposing 3x to LHS and 34 to RHS]
or, – x = – 13
or, x = 13
Hence, the required rational number
Q.17. A grandfather is ten times older than his granddaughter. He is also 54 years older than her. Find their present age.
Ans. Let the present age of granddaughter be x.
and the present age of grandfather = 10 x
According to question,
10x = x + 54
or, 10x – x = 54
or, 9x = 54
or, 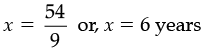
Hence, granddaughter ’s age = 6 years
and grandfather ’s age = 6 × 10 = 60 years.
Q.18. Divide : 15 (y + 3) (y2 – 16) by 5 (y2 – y – 12)
Ans. Factorising 15 (y +3) (y2 – 16),
We get, 5 × 3 × (y + 3) (y – 4) (y + 4)
On factorising, 5 (y2 – y – 12), we get 5 (y2 – 4y + 3y – 12)
= 5 [y (y – 4) + 3 (y – 4)]
= 5 (y – 4) (y + 3)
Therefore, on dividing the first expression by the second expression, we get 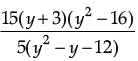
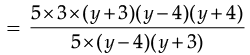
= 3 (y + 4)
Q.19. The perimeters of two squares are 40 and 96 metres respectively. Find the perimeter of another square equal in area to the sum of the first two squares.
Ans. Let the sides of two squares are a and b respectively.
4a = 40 and 4b = 96
∴ a = 10 m and b = 24 m
Given,
The perimeter of another square = Sum of area of two squares.
= Area of Ist square + Area of IInd square
= a2 + b2
= (10)2 + (24)2
= 100 + 576
= 676 m2
Hence, the perimeter of another square = 676 m.
Q.20. Prove that if x number is doubled then its cube is 8 times cube of the given number.
Ans. Let y be the double of x
i.e. y = 2x
By using on both sides
y3 = (2x)3
⇒ y3 = 23 × x3 = 2 × 2 × 2 × x3
⇒ y3 = 8x3
Q.21. We know that parallelogram is also quadrilateral. Let us also split such a quadrilateral into two triangles, find their areas and hence that of the parallelogram. Does this agree with the formula that you know already ?
Ans. AD = BC = b
CO = AO’ = h
ABCD is parallelogram divided into 2 triangles i.e., ∆ABC + ∆ACD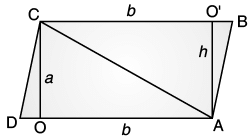
The area of parallelogram ABCD also divided into two parts = Area of ∆ABC + Area of ∆ACD
Area of ∆ABC = 1/2 × BC × AO’ {Base BC = b, height = h}
= 1/2 × b × h = 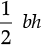 ...(i)
...(i)
Area of ∆ACD = 1/2 × AD × OC {Base AD = b, height = h}
= 1/2 × b × h ...(ii)
On adding eq. (i) & (ii) we get,
Area of ∆ABC + Area of ∆ACD = 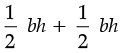
Area of ∆ABC + Area of ∆ACD = bh ...(iii)
We know that,
Area of parallelogram ABCD = b × h ...(iv)
Area of parallelogram ABCD = Area of ∆ABC + Area of ∆ACD
bh = bh
L.H.S. = R.H.S.
Q.22. Water is pouring into a cuboidal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108 m3, find the number of hours it will take to fill the reservoir.
Ans. Given, Volume of reservoir = 108 m3
Volume of water = 108 × 1000 L
= 108000 L
60 litres water filled reservoir in 1 minute
108000 litres water filled reservoir in = 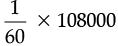
= 1800 minutes
= 30 hrs
Hence, 108000 L water filled reservoir in 30 hrs.
SECTION ‘D’ (4 marks each)
Q.23. A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base. In the following table, find the parts of base that is needed to be added.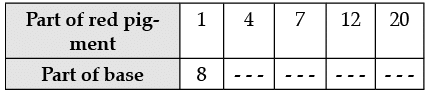
Ans. As the part of red pigment increases, part of base also increases in the same ratio. It is a case of direct proportion, we make use of the relation of the type 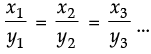
(a) Here, x1 = 1, y1 = 8 and x2 = 4
Therefore, 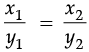
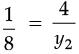
⇒ y2 = 4 × 8 = 32
(b) Here, x2 = 4, y2 = 32 and x3 = 7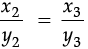
⇒ 
⇒ 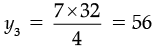
(c) Here, x3 = 7, y3 = 56 and x4 = 12, y4 = ?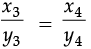
⇒ 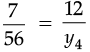
⇒ y4 = 
⇒ y4 = 96
(d) Here, x4 =12, y4 = 96 and x5 = 20, y5 = ?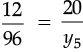
⇒ 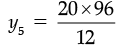
⇒ y5 = 160
The table is
Q.24. It is given that l varies directly as m.
(a) Write an equation which relates l and m.
(b) Find the constant of proportion (k), when l is 6 then m is 18.
(c) Find l, when m is 33.
(d) Find m when l is 18.
Ans. Given l ∝ m
(a) l = km, where k is a constant
(b) l = 6, m = 18
l = km
6 = k × 18
⇒ 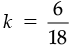
∴ 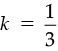
(c) m = 33, l = ?
∵ l = km
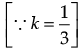
∴ l = 11
(d) l = 8, m = ?
l = km
⇒ 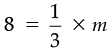
m = 24
Q.25. The perimeter of a rectangle is 240 cm. If its length is increased by 10% and its breadth is decreased by 20% we get the same perimeter. Find the length and breadth of the rectangle.
Ans. Let the length of rectangle be x
The breadth of a rectangle be b.
Perimeter of a rectangle = 2 (x + b)
2 (x + b) = Perimeter
2 (x + b) = 240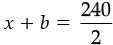
x + b = 120
or, b = 120 – x
New length = x + 10% of x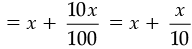
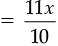
New breadth = (120 – x) – 20% of (120 – x)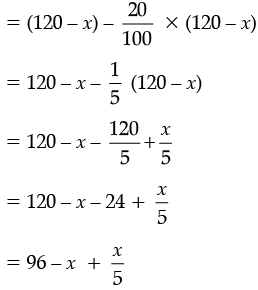
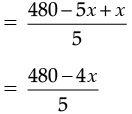
According to condition,
or, 
or, 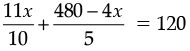
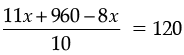
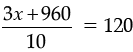
3x + 960 = 1200
3x = 1200 – 960
3x = 240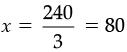
Hence,
length = x = 80 cm
breadth = 120 – x = 120 – 80 = 40 cm
Q.26. Find the area of polygon MNOPQR, if MP = 9 cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2 cm.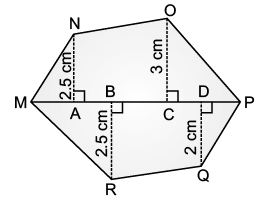
NA, OC, QD and RB are perpendiculars to diagonal MP.
Ans. It is clear from figure that polygon MNOPQR is divided into six parts, out of which four are triangles and two are trapeziums.
Area of polygon MNOPQR = Area of ∆MAN + Area of trapezium ACON + Area of ∆OCP + Area of ∆PDQ + Area of trapezium DBRQ + Area of ∆RBM ...(i)
Now, area of ∆MAN = 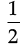 × MA × AN =
× MA × AN = 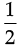 × 2 × 2.5 = 2.5 cm2
× 2 × 2.5 = 2.5 cm2
Area of trapezium ACON = 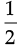 (AN + OC) × AC
(AN + OC) × AC
= 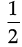 (AN + OC) × (MC – MA) [∵ AC = MC – MA]
(AN + OC) × (MC – MA) [∵ AC = MC – MA]
=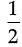 (2.5 + 3) × (6 – 2) =
(2.5 + 3) × (6 – 2) =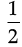 × 5.5 × 4
× 5.5 × 4
= 5.5 × 2 = 11 cm2
Area of ∆OCP = 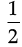 × CP × OC
× CP × OC
=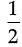 (MP – MC) × OC
(MP – MC) × OC
=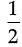 (9 – 6) × 3 =
(9 – 6) × 3 = 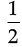 × 3 × 3 [∵ CP = MP – MC]
× 3 × 3 [∵ CP = MP – MC]
= 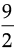 = 4.5 cm2
= 4.5 cm2
Area of ∆PDQ = 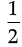 × PD × DQ
× PD × DQ
= 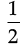 × (MP – MD) × DQ [∵ PD = MP – MD]
× (MP – MD) × DQ [∵ PD = MP – MD]
= 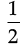 × (9 – 7) × 2 = 2 cm2
× (9 – 7) × 2 = 2 cm2
Area of trapezium DBRQ = 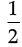 × (DQ + BR) × BD
× (DQ + BR) × BD
= 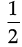 × (DQ + BR) × (MD – MB) [∵ BD = MD – MB]
× (DQ + BR) × (MD – MB) [∵ BD = MD – MB]
= 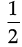 × (2 + 2.5) × (7 – 4)
× (2 + 2.5) × (7 – 4)
= 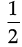 × 4.5 × 3 =
× 4.5 × 3 = 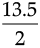 = 6.75 cm2
= 6.75 cm2
Area of ∆RBM = 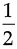 × MB × BR
× MB × BR
= 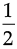 × 4 × 2.5 = 5 cm2
× 4 × 2.5 = 5 cm2
On putting all these values in Eq. (i), we get
Area of polygon MNOPQR = (2.5 + 11 + 4.5 + 2 + 6.75 + 5) cm2
= 31.75 cm2
Hence, area of polygon MNOPQR is 31.75 cm2.
Q.27. The cost of a notebook is Rs. 10. Draw a graph after making a table showing cost of 2, 3, 4 ... notebooks. Use it to find
(a) the cost of 7 notebooks.
(b) the number of notebooks that can be purchased for Rs. 50.
Ans. Let x : number of notebooks
y : cost of a notebook
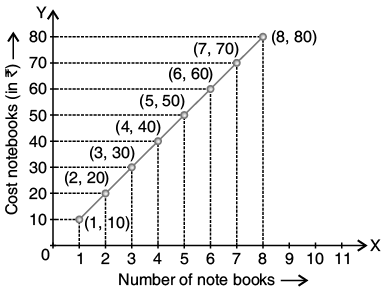
(a) The cost of 7 notebooks is equal to the coordinate of the point (7, 70), i.e. cost of 7 notebooks = Rs. 70
(b) The number of notebooks that can be purchased for Rs. 50 is equal to the abscissa of the point (5, 50).
Hence, 5 notebooks can be purchased for Rs. 50.
Q.28. In a quadrilateral ABCD, DO and CO are the bisectors of ∠D and ∠C respectively.
Prove that ∠COD = 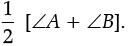
Ans. In ∆COD, we have
∠COD + ∠1 + ∠2 = 180°
⇒ ∠COD = 180° – [∠1 + ∠2]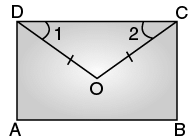
⇒ 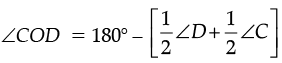
⇒ ∠COD = 180° 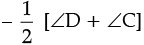
But ∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠C + ∠D = 360° – (∠A + ∠B)
⇒ ∠COD = 180° - 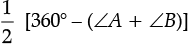
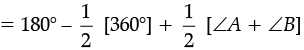
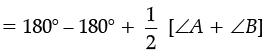
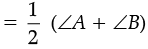
Thus, 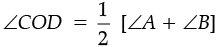
Q.29. Calculate the amount and compound interest on Rs. 10,800 for 3 years at 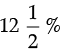 per annum compounded annually.
per annum compounded annually.
Ans. Here, P = Rs. 10800, T =3 years,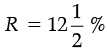

We have,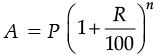
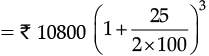
[∵ Interest compounded annually, ∴ n = 3]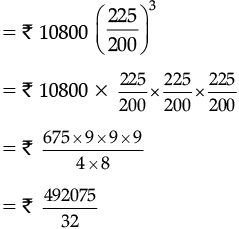
∴ Amount = Rs. 15377.34
= Rs. 15377.34
Now, Compound Interest = Rs. 15377.34 – Rs. 10800
= Rs. 4577.34
Q.30. Factorise and divide the following :
(a) (2x3 – 12x2 + 16x) / (x – 2) (x – 4)
(b) (3x4 – 1875) / (3x2 – 75)
Ans. (a) (2x3 – 12x2 + 16x) ÷ (x – 2) (x – 4)
∵ 2x3 – 12x2 + 16x = 2x (x2 – 6x + 8)
= 2x (x2 – 4x – 2x + 8)
= 2x [x (x – 4) – 2 (x – 4)]
= 2x [(x – 4) (x – 2)]
= 2x (x – 2) (x – 4)
∴ 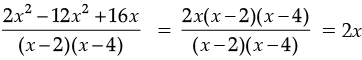
(b) (3x4 – 1875) ÷ (3x2 – 75)
∵ 3x4 – 1875 = 3 (x4 – 625)
= 3 [(x2)2 – (25)2]
= 3 [(x2 + 25) (x2 – 25)]
= 3 [(x2 + 25) (x2 – 52)]
= 3 [(x2 + 25) (x + 5) (x – 5)]
and 3x2 – 75 = 3 (x2 – 25)
= 3 [(x)2 – (5)2]
= 3 (x + 5) (x – 5)
∴ 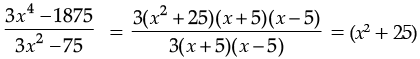
|
81 videos|423 docs|31 tests
|
FAQs on Sample Question Paper- 4 - Mathematics (Maths) Class 8
| 1. What is the exam format for Class 8 Sample Question Paper (2020-21)? |  |
| 2. How can I access the Class 8 Sample Question Paper (2020-21)? |  |
| 3. What topics are covered in the Class 8 Sample Question Paper (2020-21)? |  |
| 4. Are the questions in the Class 8 Sample Question Paper (2020-21) similar to the actual exam? |  |
| 5. How can I use the Class 8 Sample Question Paper (2020-21) to prepare for the exam? |  |





















