Second Law of Thermodynamics: Assignment | Kinetic Theory & Thermodynamics - Physics PDF Download
Q.1. Compare the efficiency of both cycle ABC and EFG. If T1 =1000K, T2 = 500K , then find 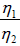 , where η1 , η2 is the efficiency of first and second cycle respectively.
, where η1 , η2 is the efficiency of first and second cycle respectively.
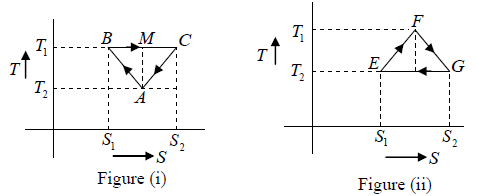
From figure (i)
η1 =
Area of ABC
η1 =
and from figure (ii)
η2 =
Hence
and
Q.2. Figure shows the PV diagram of an ideal engine. All processes are quasistatic and CP is constant. Prove that the efficiency of engine is-
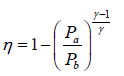
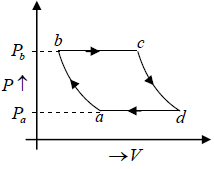
W =
=
∴
W =
=
=
∵ PV = nRT
η =
∵
Q.3. A mass of air is initially at 260oC and 700 kPa and occupies 0.028m3 . The air is
expanded at constant pressure to 0.084m3 . A polytropic process with n =1.50 is then carried out, followed by a constant temperature process which completes a cycle. All the processes are reversible.
(a) Sketch the cycle in the P-V and T - S planes.
(b) Find the heat received and heat rejected in the cycle.
(c) Find the efficiency of the cycle.
(CP = 1.005 kJ/mol .K , Cv = 0.718kJ/mol. K, R = 0.287kJ/mol. K
(a) The cycle is sketched on the P -V and T -S planes in figure given below.
Given P1 = 700 kPa, T1 = 260 + 273 = 533 K = T3 , V1 = 0.028m3 ,V2 = 0.084m3
From the ideal gas equation of state
m =
Now
= 3
∴T = 3 x 533 = 1599K
Again
= 27
Heat transfer in process 1 -2
Heat transfer in process 2 -3
=
= 19.59kJ
For process 3-1
dQ = dU + dW = dW (dU = 0)
=
= -64.53kJ
(b) Heat received in the cycle
Heat rejected in the cycle
Q2 = 19.59 + 64.53 = 84.12 kJ
(c) The efficiency of the cycle
= 1 - 0.61 = 0.39, or 39 %
Q.4. A reversible engine, as shown in figure below during a cycle of operations draws 5MJ from the 400 K reservoir and does 840 kJ of work. Find the amount and direction of heat interaction with other reservoirs.
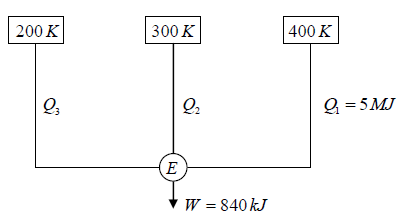
Assume heat exchange Q2 and Q3 , one at should be rejection
Energy balance, Q1 + Q2 - Q3 = W
⇒ 5000 + Q2 -Q3 = 840
⇒ -Q2 +Q3 = 4160 (i)
as for a reversible engine
⇒
⇒
⇒ -2Q2 + 3Q3 = 7500 (ii)
Solving equation (i) and (ii), we have
Q2 = -4980 kJ , Q3 = -820 kJ
Q.5. Consider an arbitrary heat engine which operates between reservoirs, each of which has the same finite temperature-independent heat capacity c . The reservoirs have initial temperatures T1 and T2 , where T2 > T1 , and the engine operates until both reservoirs have the same final temperature T3 .
(a) Give the argument which shows that 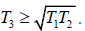
(b) What is the maximum amount of work obtainable from the engine?
(a) The increase in entropy of the total system is ΔS =
Thus
(b) The maximum amount of work can be obtained using a reversible heat engine, for which ΔS = 0 so
Q.6. One kg of H2O at 0oC is brought in contact with a heat reservoir at 100oC . When the water has reached 100oC
(a) What is the change in entropy of the water?
(b) What is the change in entropy of the universe?
(c) How could you heat water to 100oC so the change in entropy of the universe is zero
The process is a irreversible. In order to calculate the change of entropy of the water and of the whole system, we must construct a reversible process which has the same initial and final states as the process in this problem. (a) We assume the process is a reversible process of constant pressure. The change in entropy of the water is
we substitute m = 1kg , and CH2O = 4.18 J / g K into it, and find
(b) The change in entropy of the heat source is
Therefore the change of entropy of the whole system is
(c) We can imagine infinitely many heat sources which have infinites temperature difference between two adjacent sources from 0oC to 100oC . The water comes in contact with the infinitely many heat sources in turn in the order of increasing temperature. This process which allows the temperature of the water to increase from 0oC to 100oC is reversible therefore ΔS=0 .
Q.7. Find the efficiency of the cycle if He is used as a working fluid. (Assuming ideal gas). Given that for 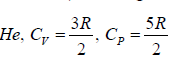
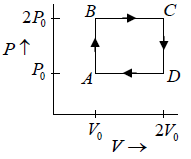
W = area =ABCDA= P0V0

Heat supplied =
as PV = RT ⇒ dPV = d(RT)
or PdV +VdP= RdT
or PdV = RdT (for constant P, dP =0 )
and VdP = RdT (for constant volume dV = 0 )
η =
Q.8. An inventor claims to have developed an engine giving 9kW with input of 1000kJ /min between temperature of 30oC and -40oC . Discuss the possibility of the claim.
Maximum efficiency is the Carnot engine efficiency between the given temperature limits.
= 0.422
For given engine η =
= 0.54
As this is more than Carnot efficiency between some temperature limit, hence not possible.
Q.9. Efficiency of a Carnot cycle is 1/6. By lowering the temperature of the sink by 65K , it increases to 1/3. Find sink temperature.
(for a rev. cycle)
on solving T2 = 325K .
Q.10. In the cycle ABC, heat added to system in process AB&BC are 400 J & 100 J
respectively. Heat rejected during CA is 460 J . Find its efficiency.
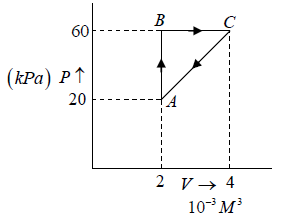
W = area of cycle =
= 40J
Heat added = 400 + 100 = 500 J (as W = Q1 - Q2 = 500 - 460 = 40 J ) verify
η = 8%
Q.11. Find the efficiency of cycle ABC .
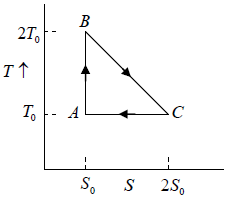
As AB is adiabatic ( Q = 0 ) , heat is added in BC and rejected in AC .
η =
Q.12. Find the efficiency of cycle ABCD. For gas Cv = 3R/2. Heat is added and rejected at constant volume and constant pressure.
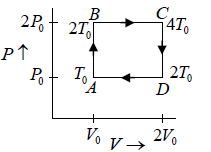
Heat added during AB = CV dT
Total heat added =
Heat rejected =
|
6 videos|20 docs|32 tests
|
FAQs on Second Law of Thermodynamics: Assignment - Kinetic Theory & Thermodynamics - Physics
| 1. What is the second law of thermodynamics? |  |
| 2. How is the second law of thermodynamics related to energy transfer? |  |
| 3. What is entropy and how does it relate to the second law of thermodynamics? |  |
| 4. Can the second law of thermodynamics be violated? |  |
| 5. How does the second law of thermodynamics impact real-life applications? |  |




















 = 3
= 3 = 27
= 27


 = 19.59kJ
= 19.59kJ
 = -64.53kJ
= -64.53kJ = 1 - 0.61 = 0.39, or 39 %
= 1 - 0.61 = 0.39, or 39 %
 ⇒
⇒ 














 = 0.422
= 0.422 = 0.54
= 0.54
 (for a rev. cycle)
(for a rev. cycle) 
 = 40J
= 40J η = 8%
η = 8%
 η =
η = 

























