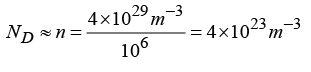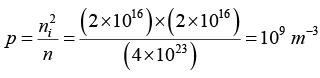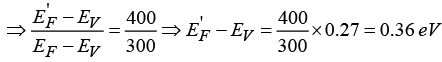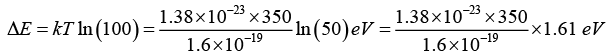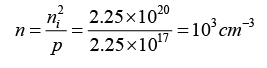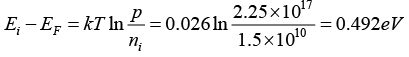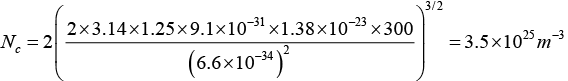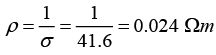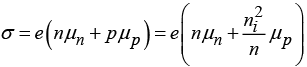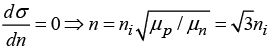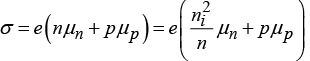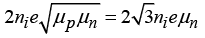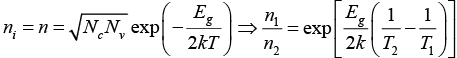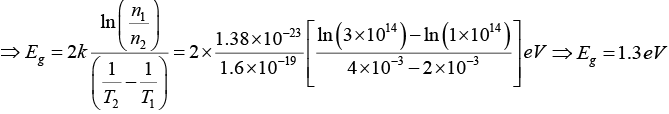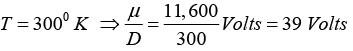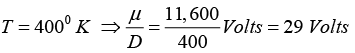Semiconductor Physics: Assignment | Solid State Physics, Devices & Electronics PDF Download
Q.1. Pure silicon at 300 K has equal electron and hole concentration of 2 x 1016 m-3. It is doped by nitrogen to the extent one part in 106 silicon atom. If the density of silicon is 4 x 1029 m-3, then find the electron and hole concentration in the doped silicon.
Donor ion concentration
According to Law of Mass Action, n.p = ni2
Q.2. In a p-type semiconductor, the Fermi level is 0.27 eV above the valance band at room temperature of 300 K . If the temperature is increased to 400 K , then find the new position of the Fermi-level. (Assume effective density of states to be independent of temperature).
EF-EV = kT ln NV/NA ⇒ 0.27 = 300k In NV/NA and E'F-EV = 400K In NV/NA
Q.3. The acceptor concentration in a sample of p -type silicon is increased by a factor of 50. Find the shift in the position of the Fermi level at 350K.
EF-EV = kT ln (NV/NA) and E'F - EV = kT In (NV/50NA) = kT In (NV/NA) - kT In (50)
Thus shift is
⇒ ΔE = 486 x 10-4 eV = 48.6 meV
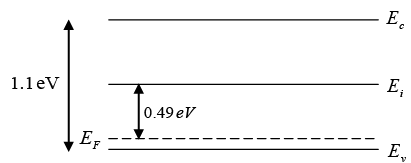
Q.4. A Si sample is doped with 2.25x1017 Al atoms/cm3 at 300 K. The intrinsic carrier concentration at 300 K is 1.5 x 1010 cm-3.
(a)What is the equilibrium electron and hole concentration at 300 K?
(b) Where is EF relative to Ei?
Since NA>>ni we can approximate ni and p = 2.25 x 10 17Al
Q.5. For a given semiconductor the effective mass of the electron is 1.25me and the Fermi level is 0.3 eV below the conduction at 300 K . Determine the concentration of electrons in conduction band.
At 300 K,
⇒ n = 3.5 x 1025 exp[-0.3x1.6x10-19 / 1.38x10-23x 300] = 32 x 1019m-3
Q.6. Consider an intrinsic semiconductor with energy band gap of 0.72 eV at 300 K . What will be shift in position of Fermi-level from the middle of the band gap if effective mass of hole is five times the effective mass of electrons?
Q.7. Consider an intrinsic semiconductor with energy band gap of 1.43 eV , effective density of states in conduction band is 1.54 x 1024 m-3 and effective density of states in valance band is 1.3 x 1025 m-3 at 300 K.
(a) Determine the intrinsic carrier concentration of the semiconductor.
(b) Determine the effective masses of electrons and holes.
(b) At 300 K,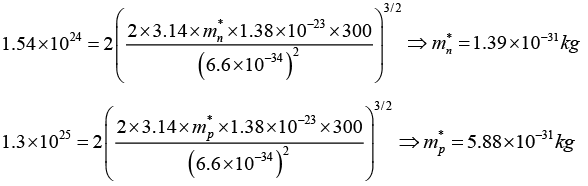
Q.8. A sample of Si has electron and hole mobilities of 0.13 and 0.05 m2V-1s-1 respectively at 300K.
(a) It is doped with P and Al with doping densities of 3.5 x 1021/m3 and 1.5 x 1021/m3 respectively. Find the resistivity of doped Si sample at 300K.
(b) It is doped with Ga and N with doping densities of 3.5 x 1021/m3 and 1.5 x 1021/m3 respectively. Find the conductivity of doped Si sample at 300 K.
(a) Resulting doped crystal is n-type and nn = (3.5 - 1.5) x 1021/m3 = 2 x 1021/m3
σ = e(nnμn + pnμp) ≈ ennμn = 1.6 x 10-19 x 2 x 1021 x 0.13 = 41.6Ω-1m-1
(b) Resulting doped crystal is p-type and pp = (3.5-1.5) x1021/m3 = 2 x 1021/m31.6 x 10-19 x 2 x 1021 x 0.05 = 16Ω-1m-1.
Q.9. Consider an extrinsic semiconductor with intrinsic concentration of ni. If μp and μn are mobility of holes and electron where μp = 3μn then
(a) Find the electron concentration at which semiconductor has minimum conductivity
(b) Find the hole concentration at which semiconductor have minimum conductivity
(c) Find minimum conductivity σmin.
(a) Conductivity
For minimum conductivity,
(b) Conductivity
For minimum conductivity,
(c) Thus, σmin =
Q.10. In an intrinsic semiconductor, the free carrier concentration n (in cm-3) varies with temperature T (in Kelvin) as shown in the figure below.
If n1 = 3 x 1014m-3 and n2 = 1 x 108m-3 and 1/T1 = 2 x 10-3K-1 and 1/T2= 4 x 10-3K-1.
Find the band gap energy of the semiconductor material. (Assume effective density of states and band gap energy to be independent of temperature).
Since
Q.11. Find the ratio of mobility (μ) and diffusion coefficient (D) for electrons in a semiconductor at temperature T = 270C and T = 1270C.
where VT is the ‘Volt-equivalent of temperature’.
At temperature
At temperature
Q.12. The electron concentration in a sample of uniformly doped n-type silicon 300 K varies linearly from 1017/cm3 at x = 0 to 8x1016/cm3 at x = 2μm. Assume a situation that electrons are supplied to keep this concentration gradient constant with time. If electronics charge is 1.6 x 10-19 C and the diffusion constant Dn = 35cm2/s, find the current density in the silicon, if no electric field is present.
Q.13. Determine the wavelength of light emitted from LED which is made up of GaAsP semiconductor whose forbidden energy gap is 1.875 eV. Mention the colour of the light emitted (Take h = 6.6 × 10-34 Js).
Eg = hc / λ
Therefore
λ = hc / Eg = 6.6 × 10−34 × 3 × 108 / 1.875 × 1.6 × 10−19
= 660 nm
The wavelength 660 nm corresponds to red colour light.
Q.14. In a transistor connected in the common base configuration, α = 0.95 , IE = 1 mA . Calculate the values of IC and IB.
α = IC/IE
IC = α IE = 0.95 × 1 = 0.95 mA
IE = IB + IC
∴ IB = IC − IE = 1 − 0.95 = 0.05 mA
Q.15. Calculate the range of the variable capacitor that is to be used in a tuned-collector oscillator which has a fixed inductance of 150 μH. The frequency band is from 500 kHz to 1500 kHz.
Q.16. In the given figure of a voltage regulator, a Zener diode of breakdown voltage 15V is employed. Determine the current through the load resistance, the total current and the current through the diode. Use diode approximation.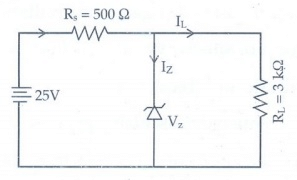
Voltage across RL(VO) = Vz = 15V
Voltage across RS(VRS) = 25 - 15 = 10V
current through RL is
IL = V0/RL = 15 / 3 × 103 = 5 × 10-3 A
IL = 5 mA
Current through RS is
I = VRS/RS = 10/500 = 20 × 10-3A
I = 20mA
Current through Zener diode is
IZ = I-IL = (20 - 5) × 10-3 Iz = 15mA
|
91 videos|21 docs|25 tests
|
FAQs on Semiconductor Physics: Assignment - Solid State Physics, Devices & Electronics
| 1. What is semiconductor physics? |  |
| 2. How do semiconductors work? |  |
| 3. What is doping in semiconductor physics? |  |
| 4. What are the primary applications of semiconductor physics? |  |
| 5. What are the challenges in semiconductor physics research? |  |