Sequences of Real Numbers- I | Mathematics for Competitive Exams PDF Download
Introduction (Sequences of Real Numbers)
By a sequence, we mean an arrangement of numbers in a definite order according to some rule. We denote the terms of a sequence by a1, a2, a3, etc., the subscript denotes the position of the term.
In view of the above a sequence in the set X can be regarded as a mapping or a function f : N → X defined by
f(n) = an ∀ n ∈ N
Domain of f is a set of natural numbers or some subset of it denoting the position of term. If its range denoting the value of terms is a subset of R real numbers then it is called a real sequence. A sequence is either finite or infinite depending upon the number of terms in a sequence. We should not expect that its terms will be necessarily given by a specific formula. However, we expect a theoretical scheme or rule for generating the terms.
Sequence following certain patterns are more often called progressions. In progressions, we note that each term except the first progresses in a definite manner.
A sequence of real numbers is a function whose domain is a set of the form {n ∈ 𝕫 I n ≥ m} where m is usually 0 or 1. Thus, a sequence is a function f : N → R. Thus a sequence can be denoted by f(m), f(m + 1), f(m + 2), ... Usually, we will denote such a sequence by (ai)∞i=m or {am, am+1, am+2, ....}
where ai = f(i). If m = 1, we may use the notation {an}n∈N.
Definition: Every function defined from the set N of natural numbers to a non-empty set X is called a sequence.
Real Sequence
Every function defined from the set N of natural numbers to a non-empty subset X of the set of real numbers R is called a real sequence, denoted by f : N → R.
Thus the real sequence f is set of all ordered pairs {n, f(n)} I {n = 1, 2, 3, ...} i.e., set of all pairs (n, f(n)) with n a positive integer.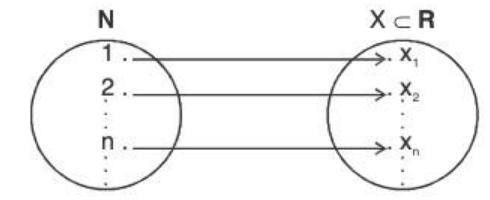
If f : N → R is a sequence, then for each n ∈ N, f(n) is a real number. It is conventional to write f(n) as fn.
Notations: Since the domain of a sequence is always the same (the set of positive integers) a sequence may be written as {f(n)} instead of {n, f(n)}.
Example. The sequence {1, 1/2, 1/3, 1/4, 1/5, ...} is written as {1/n}∞n=1. This sequence can be thought of as an ordinary function f(n) = 1/n.
Example. Consider the sequence given by an = (-1)n for n ≥ 0. The terms of the sequence look like, { 1, - 1, 1, - 1, 1, - 1, ...}. Note that the function has domain N but the range is { - 1, 1}.
Example. Consider the sequence an = cos {nπ/3}, n ∈ N. The first terms in the sequence is cosπ/3 = cos 60o = 1/2 and the sequence looks like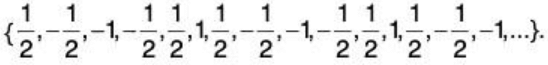
Note that the function takes on only a finite number of values, but the sequence has an infinite number of elements.
Example. If an = n1/n, n ∈ N, the sequence is
1, √2, 31/3, 41/4, ....
Example. Consider the sequence bn = (1 + 1/n)n, n ∈ N. This is the sequence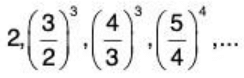
Representation of A Sequence
The real numbers x1, x2, ..., xn, ... are called the terms or elements of the sequence. x1, is called the first term, x2 the second term, ... , xn the nth term of the sequence {xn}. It is denoted by {x1, x2, x3, ... xn, ... } or {xn} or {xn}.
Example.
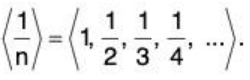

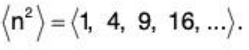
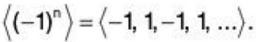
- A sequence (an) may be defined by a recursion formula:
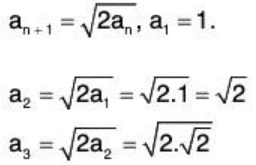
Here the terms of the sequence are 1, √2,√2√2, .....
Range of a Sequence
The set of all the distinct elements of a sequence is called the range set of the given sequence.
Example. The range sets of the sequences given in Example are respectively
(i) {1, 1/2, 1/3, ...}
(ii) {0, 2}
(iii) {1, 4, 9, ...}
(iv) {-1, 1}
(v) {1, √2, √2√2, ...}
Note: The range set of a sequence may be finite or infinite but the sequence has always an infinite number of elements.
Particular Sequences
(a) Constant Sequence: If the nth term of the sequence is constant i.e. an = c ∈ R, ∀ n, then the sequence obtained (c, c, c, ...) is known as constant sequence.
Example.
(5, 5, 5, 5, ... ) = (5)
(0, 0, 0, 0, ... ) = (0)
(b) Identity Sequence: If the nth term of the sequence is an = n, then the obtained sequence is called Identity sequence.
Example. (1, 2, 3,.....)
Equal Sequence
Two sequences <an> and <bn> are equal, if their nth terms are equal, i.e. an = bn, ∀n ∈ N
Bounded and Monotone Sequences
Bounded Sequence
Bounded above: A sequence (an) is said to be bound above, if ∃ a real number K s.t.
an ≤ K ∀ n ∈ N. K is called an upper bound of the sequence (an).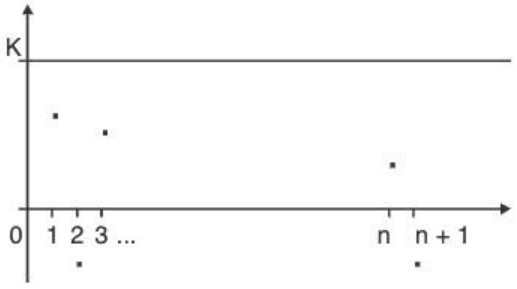 Bounded above sequence
Bounded above sequence
Bounded below: A sequence (an) is said to be bounded below, if ∃ a real number k s.t.
K ≤ an ∀ n ∈ N. K is called an lower bound of the sequence (an).
Bounded: A sequence (an) is said to be bounded, if it is both bounded above and bounded below.
Equivalently, (an) is bounded, if there exist two real numbers k and K such that k ≤ an < K ∀ n ∈ N.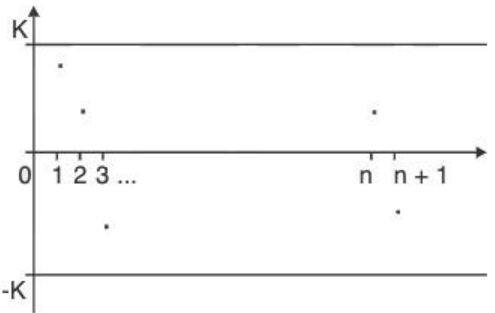 Bounded sequence
Bounded sequence
Examples
1. (1/n) = (1, 1/2, 1/3, 1/4, ..) is bounded, as 0 < 1/n ≤ 1 ∀ n ∈ N.
2. (1 + (-1)n) = (0, 2, 0, 2, ...) is bounded.
Supremum and Infimum of a Sequence
The minimum value of the upper bounds of sequence is known as Supremum or least upper bound (lub) of a sequence.
The greatest of the lower bounds of a sequence is known as the Infimum or greatest lower bound (gIb) of a sequence.
Examples
- The sequence {n2} is bounded below: n2 > 0 ∀ n ∈ N but not bounded above;
- The sequence {-n} is bounded above: -n < 0 ∀ n ∈ N but not bounded below;
- The sequence {( - 1)n + 1} is bounded : l( - 1)n + 1I ≤ 2 ∀ n ∈ N.
Infinitely large sequences represent an important subset of unbounded sequences.
Definition: A sequence {an} is called infinitely large if ∀ K ∈ R ∃ nK ∈ N such that lanl > K ∀ n ≥ nK.
As an example, we show that the sequence {(-1)n n3} is infinitely large.
Indeed, for any number K, we can find nk such that l(-1)n n3l > K ∀ n ≥ nK.
To this end, we solve the inequality n3 > K, and n > ∛K. t
Let nk = [∛K] + 1, where [c] is the integer part of c.
Then for n ≥ nK we obtain.
n ≥ nK > ∛K ⇒ n3 > K ⇒ |(-1)n n3| > K.
From above Definition it follows that any infinitely large sequence is unbounded. However, the converse is not true: there exist unbounded sequences that are not infinitely large.
For example, such is the sequence {(1 - (-1)n)n}.
Definition. A sequence {an} is called infinitely small if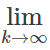 an = 0,
an = 0,
that is for any ε > 0 there exists nε such that
|an| < ε ∀ n ≥ nε
For example, the sequence {qn} for Iql < 1 is infinitely small. Indeed, for any ε > 0 let us find nε such that lqnl < ε ∀ n ≥ nε. To this end, we solve the inequality lqnl < ε, assuming that 0 < ε < 1 (for ε ≥ 1, this inequality is clearly true for any n ∈ N):
n In(|q|) < In ε ⇒ n > Inε/In|q|, nε = [Inε/In|q|] + 1,
where lnε < 0, and In Iql < 0, since ε < 1, and Iql < 1. Thus, for n ≥ nε we have
n ≥ nε > In ε/In|q| < Inε ⇒ |q|n < ε.
The fact that {an} is not infinitely small means the following there exists ε0 > 0 such that for any n ∈ N there exists kn > n with |akn| > ε0.
Unbounded Sequence
Sequence which is either unbounded above or below is called an unbounded sequence.
Monotone Sequences
- Monotonicaliy Increasing: A sequence (an) = (a1, a2, a3, ..., an, ...) is said to be monotonically increasing, if an+1, ≥ an ∀ n ∈ N.
- Monotonically Decreasing: A sequence (an) = (a1, a2, a3, .... an, ...> is said to be monotonically decreasing, if an+1, ≤ an ∀ n ∈ N.
- Monotonic: A sequence (an) is said to be monotonic (or monotone) if it is either monotonically increasing or monotonically decreasing.
- Strictly monotonic sequence: either strictly increasing or strictly decreasing. In particular, monotonically increasing is the same as increasing, strictly monotonically increasing the same as strictly increasing.
Examples
- The sequence (2n) = (2, 4, 8, 16, ...) is monotonically increasing.
Since a1 = 2 < a2 = 4 < a3 = 8 < ...... - The sequence
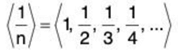 is monotonically decreasing.
is monotonically decreasing.
Since a1 = 1 > a2 = 1/2 > a3 = 1/3 > ....... - The sequence
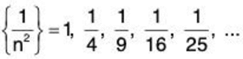 is a bounded monotone decreasing sequence, Its upper bound is greater than or equal to 1, and the lower bound is any non-positive number. The least upper bound is number one, and the greatest lower bound is zero, that is,
is a bounded monotone decreasing sequence, Its upper bound is greater than or equal to 1, and the lower bound is any non-positive number. The least upper bound is number one, and the greatest lower bound is zero, that is,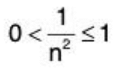
for each natural number n. - The sequence
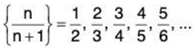 is a bounded monotone increasing sequence. The least upper bound is number one, and the greatest lower bound is 1/2, that is,
is a bounded monotone increasing sequence. The least upper bound is number one, and the greatest lower bound is 1/2, that is,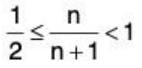
for each natural number n. - The sequence
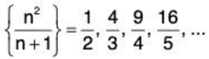 is an unbounded sequence, because it does not have a finite upper bound.
is an unbounded sequence, because it does not have a finite upper bound. - Monotone increasing sequences:
{n}= 1, 2, 3, ...
- Monotone decreasing sequences:
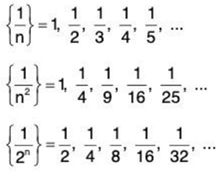
Eventual nature of a sequence
Definition. A sequence {an} of real numbers is called non-decreasing if an ≤ an+1 for all n, and it is called non-increasing if an ≥ an+1 for all n. It is called strictly increasing if an < an+1 for all n, and strictly decreasing if an > an+1 for all n.
A sequence {an} of real numbers is called eventually non-decreasing if there exists a natural number N such that an ≤ an+1 for all n ≥ N, and it is called eventually non-increasing if there exists a natural number N such that an ≥ an+1 for all n ≥ N. We make analogous definitions of “eventually strictly increasing” and "eventually strictly decreasing.”
Limit Point of a Sequence
Let {an} be any sequence and α ∈ N we say a is limit point of {an} if every neighbourhood of a contains infinite members of the sequence {an}.
i.e. for any δ > 0
an ∈ (α - δ, α + δ) for infinite values of n.
Examples
(i) an = (-1)n
α = -1
for any δ > 0
an ∈ (-1 - δ, -1 + δ) ∀ n = 2k - 1, k = 1, 2, ....
∴ -1 is a limit point.
α2 = 1.
for any δ > 0
an ∈ (1 - δ, 1 + δ) ∀ n = 2k, k = 1, 2, ...
∴ 1 is a limit point.
{an} has two limit points {-1, 1}.
(ii)
α = 2
for any δ > 0
an ∈ (2 - δ, 2 + δ) ∀ n = 1 or prime
∴ 2 is a limit point.
Let p be any prime,
for any δ > 0
an ∈ (p - δ, p + δ) ∀ n = pk, = 1, 2, ...
∴ p is the limit point of an.
Hence, every prime no. is a limit point of {an}.
As set of prime no. are infinite
∴ {an} has infinite no. of limit points.
Theorem: Every limit point of the range set of a sequence is limit point of a sequence.
Solution: Let S be range set of sequence {an}.
i.e. S = range of {an}
Let α ∈ S'
for ε > 0
(α - ε, α + ε) ∩ S\{α} has infinite no. of points
Let q ∈ (α - ε, α + ε) ∩ S\{α}
⇒ q ∈ (α - ε, α + ε) and q ∈ S
As q ∈ S
⇒ q = ak for some k ∈ N
So ak ∈ (α - ε, α + ε)
Hence, (α - ε, α + ε) contains infinite no. of terms of sequence
∴ α is limit point of sequence {an} Proved
Remark: A real no. is a limit point of sequence ⇔ it appears in the sequence infinite many times or it is the limit point of the range set.
Bolzano-Weierstrass Theorem
Theorem: Every bounded sequence has a limit point.
Proof: Let (an) be a bounded sequence.
Let S = {an : n ∈ N} be its range.
Since the sequence is bounded, therefore, its range S is also bounded.
Case I. Let S be a finite set.
Then there must exist at least one element α ∈ S such that
an = α for an infinite number of values of n.
For any ε > 0, the nbd. (α - ε, α + ε ) of α, contains an = α, for an infinite number of values of n. Therefore, α is a limit point of (an).
Case II. Let S be an infinite set.
The range S being an infinite bounded set has a limit point, say p, So each nbd (p - ε, p + ε) of p contains an infinite number of elements of S
i.e., an ∈ (p - ε, p + ε) for an infinite number of values of n.
Hence p is a limit point of <an>.
Remark
An unbounded sequence may or may not have a limit point.
Counter example, Since an = n is an unbounded sequence with no limit point and an = 1, if n is even; an = n, if n is odd is an unbounded sequence with a limit point 1.
Limit of a Sequence
Definition
A sequence <an> is said to have a limit 'l' if for sufficiently large values of n, | an - l I can be made as small as we please.
l is the limit of a sequence, if for given ε > 0 ∃ no ∈ N s.t.
I an - I I < ε, ∀ n > no
or lim an = I
Some Important Limits
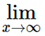 (1 + 1/n)n = e
(1 + 1/n)n = e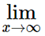 n1/n = 1,
n1/n = 1, 1/np = 0, when p > 0 and p ∈ R
1/np = 0, when p > 0 and p ∈ R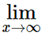 rn = 0, when I r I < 1 and r ∈ R
rn = 0, when I r I < 1 and r ∈ R r1/n = 1, when r > 0 and r ∈ R
r1/n = 1, when r > 0 and r ∈ R
Example 1: Let an = 1/n, and let us show that lim an = 0.
Solution: Given an ε > 0, let us choose a N such that 1/N < ε.
Now, if n ≥ N, then we have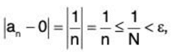
which is exactly what we needed to show to conclude that lim an = 0.
Example 2: Let an = (2n + 1)/(1 - 3n), and let L = -2/3. Let us show that L = lim an.
Solution: Indeed, if ε > 0 is given, we must find a N, such that if n ≥ N then lan + (2/3)l < ε.
Let us examine the quantity lan + 2/3I. Maybe we can make some estimates on it, in such a way that it becomes clear how to find the natural number N.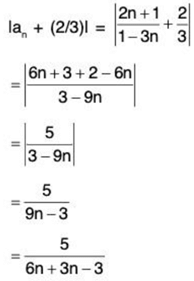
≤ 5/6n
≤ 1/n,
for all n ≥ 1. Therefore, if N is an integer for which N > 1/ε, then
lan + 2/3I < 1/n ≤ 1/N < ε,
whenever n ≥ N, as desired.
Example 3: Let an = 1/√n, and let us show that lim an = 0.
Solution: Given an ε > 0, we must find an integer N that satisfies the requirements of the definition. It's a little trickier this time to choose this N. Consider the positive number ε2. We know, that there exists a natural number N such that 1/N < ε2. Now, if n ≥ N, then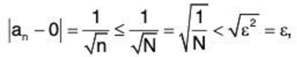
which shows that 0 = lim 1 /√n.
Theorem: Prove that a bounded sequence with a unique limit point is convergent.
Proof: Let I be the unique limit point of a bounded sequence <an>. Then for any ε > 0.
an ∈ (I - ε, I + ε) for infinitely many values of n.
We show that there exists only finitely many values of n, say m1, m2, ..., mk such that am1 ,am2, ... amk do not belong to (I - ε , I + ε) reason being the infinitely many terms of the given sequence not belonging to (I - ε , I + ε) will have a limit point other then I (by Bolzano-Weierstrass Theorem), which is a contradiction.
Let m - 1 = max {m1, m2, ... , mk}. It follows that
an ∈ (I - ε, I + ε) for all n ≥ m
i.e. lan - II < ε for all n ≥ m.
Hence <an> is convergent to I.
Limit Superior and Limit Inferior of Sequence
Let {an} be a bounded sequence then the sequence has the least and the greatest limit point.
The least limit point of {an} is called limit infinite of {an} and is denoted by  inf an.
inf an.
Note: 1. If {an} is unbounded above the 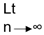 sup an = ∞
sup an = ∞
If {an} is unbounded below then 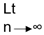 inf an = -∞
inf an = -∞
2. Since the the greatest limit point of sequence {an} ≥ the least limit point of sequence {an}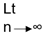 sup an ≥
sup an ≥ 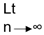 inf an.
inf an.
Example. (i) an = (-1)n.
Set of limit point = {-1, 1}
∴ 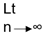 sup an = 1 and
sup an = 1 and 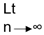 inf an = -1.
inf an = -1.
(ii) an = 1/n
Set of limit point = {0}
∴ 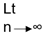 sup an = 0 =
sup an = 0 = 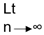 inf an.
inf an.
(iii) an = (-1)n
As sequence is neither bounded above nor bounded below.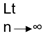 sup an = + ∞ and
sup an = + ∞ and 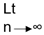 inf an = - ∞
inf an = - ∞
Note:
If sequence is bounded below theninf an = infimum of set of limit point of sequence an.
If sequence is bounded above thensup an = supremum of set of limit point of sequence an.
If sequence is bounded thensup an = supremum of set of limit point of sequence an.
inf an = infimum of set of limit points of sequence an.
Classification of Sequence
1. A sequence is said to be convergent ⇔ 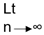 sup an =
sup an = 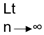 inf an (finitely)
inf an (finitely)
2. A sequence is said to be divergent ⇔ 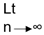 sup an =
sup an = 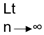 inf an (infinitely)
inf an (infinitely)
3. A sequence is said to be oscillatory ⇔ 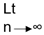 sup an ≠
sup an ≠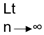 inf an.
inf an.
Important
A sequence of purely irrational number can converge to a rational number And, a sequence of purely rational number can converge to a irrational number.
Let α ∈ Qc
for any n ∈ N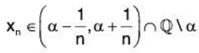
then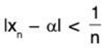
Any By Archimedean property; for any ε > 0
∃ m ∈ N such that
From (1) & (2);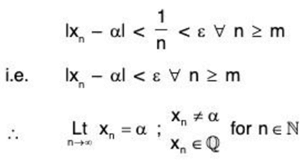
Hence, sequence of purely rational number can converge to irrational number. Similarly, we can prove the other statement.
Convergent and Divergent Sequence
Convergent Sequence
Definition: A sequence of real numbers is said to converge to a real number L if for every ε > 0 there is an integer N > 0 such that if k > N then lak - L| < ε. The number L is called the limit of the sequence.
If {ak} converges to L we will write 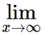 ak = L or simply ak → L. If a sequence does not converge, then we say that it either diverge or oscillate.
ak = L or simply ak → L. If a sequence does not converge, then we say that it either diverge or oscillate.
Note that the N in the definition depends on the ε that we were given. If you change the value of ε then you may have to "recalculate” N.
Consider the sequence an = n/2n, n ∈ N. Now, if we look at the values that the sequence takes 1/2, 2/22, 3/23, 4/24, .... 
we might think that the terms are getting smaller and smaller so maybe the limit of this sequence would be 0. Let’s take a look and compare how N would vary as ε varies. Let’s start with some simple small numbers and let ε be 0.1, 0.01, 0.001, and 0.0001, and 0.00001. For ε = 0.1, we need to find an integer N so that
Look in the table of values here and we see that for N = 6 we have satisfied the above condition. Following this we get the following by using a calculator or a computer algebra system:

A sequence is said to be convergent if its limit is finite.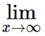 Xn = I
Xn = I
Definition: A sequence <an> converges to any number I iff for given ε > o ∃n0 ∈ N (depending on ε)
lan - I I < ε ∀ no > n
Divergent Sequence
A sequence is said to be divergent if 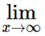 an = + ∞ or - ∞
an = + ∞ or - ∞
Definition: A sequence is said to be divergent if and only if for any k > 0 ∃ a no. no s.t.
an > k ∀ n > no.
For Example,
(i) The sequence {an} = {n} = {1, 2, 3, 4, 5, 6, 7, ...} diverges since its limit is infinity (∞).
(ii) The sequence {an} = {n2} = {1, 4, 9, 16, 25, 36, 49, ...} diverges
(iii) Vn = (-1)n:
This sequence diverges whereas the sequence is bounded:
- 1 ≤ Vn ≤ 1
(iv) Another example would be xn = In n, since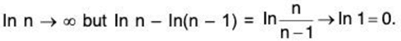
(v) The sequence {sin(nπ/2)}n≥1 diverges because the sequence is { 1, 0, - 1. 0, 1, 0, ...}, and hence it does not converge to any number.
Oscillatory Sequence
The sequence which is neither convergent nor divergent is said to be an oscillatory sequence, i.e., Sequences that tend to nowhere are always oscillating sequences.
For ex. (i). (- 1)n → nowhere (ii). (- 2)n → nowhere
We remark that an unbounded sequence that does not diverge to ∞ or - ∞ oscillates infinity.
For example, the sequences {( - 1)n n}, {(-1)n n2}, {(-n)n} are all unbounded and oscillate infinitely.
Theorem: Every convergent sequence is bounded.
Proof: Let us suppose that <an> be a convergent sequence and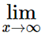 an = I.
an = I.
Let ε = 1. Then there exists a positive integer m such that
I an - I I < 1 ∀ n ≥ m
⇒ I - 1 < an < I + 1 ∀ n ≥ m. (1)
Let K = max { a1, a2, ...... am-1, I + 1}, (2)
k = min {a1, a2, .... am-l, I - 1}. (3)
From (1), (2), (3), we get
k ≤ a ≤ K ∀ n.
Hence <am> is bounded.
Converse of this theorem is not true, counter example an = (-1)n
Theorem: If 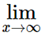 an = I, then I is the unique limit point of <an>
an = I, then I is the unique limit point of <an>
Proof: Since 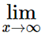 an = I, there exists a positive integer i such that
an = I, there exists a positive integer i such that
|an - I| < ε / 2 ∀ n ≥ i. (1)
Since I' is a limit point of <an>, there exists a positive integer j such that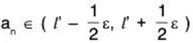 for n > j (i.e., for infinitely many values of j).
for n > j (i.e., for infinitely many values of j).
⇒ lan - I'I < ε / 2 for n > j. (2)
Let N > max {i, j}
Since N > i, so by (1), laN - II < ε / 2 (3)
And since N > j , so by (2), laN, - I’I < ε / 2 (4)
Now |I - I’| == l(aN - I') - (aN- I)|
≤ laN- I’| + |aN - I| <ε/2 + ε/2 = ε, by (3) and (4).
Since c is arbitrarily small and |I - I’| < ε, so |I - I’| = 0 i.e., I = I’.
Hence I is the unique limit point of <an>.
Converse of this theorem also doesn't hold, such as an = 1, if n is even; an = n, if n is odd is a sequence with a unique limit point 1 but it does not converge to 1.
Theorem: A necessary and sufficient condition for the convergent of a monotonic sequence is that it is bounded.
Proof: The condition is necessary (⇒)
Let <an> be a monotonic and convergent sequence.
We know that every convergent sequence is bounded.
Hence <an> is bounded.
The condition is sufficient (⇐)
Let <an> be a monotonic and bounded sequence
Since <an> is monotonic, we may suppose that <an> is monotonically increasing. We shall prove that <an> is convergent.
Let S = {an : n ∈ N} be the range of <an>.
Then S is bounded above, since the sequence <an> is bounded above By order completeness property, S has the least upper bound.
Let p = l.u.b. S. We shall show that <an> converges to p. Let ε > 0 be any number. Since p - ε < p, p - ε cannot be an upper bound of S and so there exists some am ∈ S such that am > p - ε.
Since <an> is monotonically increasing, therefore
an ≥ am ∀ n ≥ m
or an ≥ am > p - ε ∀ n ≥ m or an > p - ε ∀ n ≥ m .... (i)
Also p = sup S ⇒ an ≤ p < p + ε ∀ n. ...(ii)
∴ p - ε < an < p + ε ∀ n ≥ m, using (i), (ii)
or I an — p | < ε ∀ n ≥ m
Hence <an> converges to p.
Theorem: (i) Every monotonically increasing sequence which is bounded above converge to its least upper bound.
(ii) Every monotonically decreasing sequence which is bounded below converge to its greatest lower bound.
Proof, (i) Let {an} be monotonically increasing sequence which is bounded above.
Let u be the least upper bound of sequence {an}
Let ε > 0
Since u - ε < u
∴ u - ε is not an upper bound of {an}
⇒ ∃ m ∈ R s. that an > u - ε.
Since an is monotonically increasing
an ≥ am > u — ε ∀ n ≥ m
⇒ an > u - ε ∀ n ≥ m ...(1)
Also, u is least upper bound of {an}
an ≤ u ∀ n ∈ N
⇒ an ≤ u + ε ∀ n ≥ m ...(2)
From (1) & (2)
u - ε < an < u + ε ∀ n ≥ m
⇒ lan - u| < ε ∀ n ≥ m
∴ an → u.
Similarly, we can prove (2).
Example 1: Find the value of α for which the sequence <an> converges to 1 where a1 = α, an+1 = 1/2 (an2 + an) for n ≥ 1
Solution: <an> = <1, 1, 1, ... >, if α = 1. Hence an → 1, if α = 1.
Example 2: If the sequence (an), where an = 1 + 1/3 + 1/32 + ... + 1/3n-1 + .... + 1/3n-1 converges then what is the value of 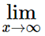 an?
an?
Solution: We have an = 1 + 1/3 + 1/32 + .... + 1/3n-1, which is a geometric progression with common ratio 1/3.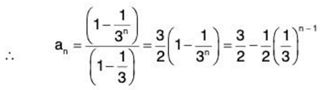
Now,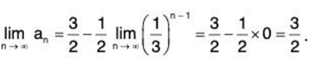 [ ∵ lim rn = 0, if I r I < 1].
[ ∵ lim rn = 0, if I r I < 1].
Hence <an> is convergent and  an = 3/2.
an = 3/2.
Example 3: The sequence (xn) is bounded and monotone where x1 = √2 and Xn+1 = √2xn, then it converges to 2.
Solution: Observe that x2 > x1. Since X2n+1 - Xn2 = 2(xn - xn-1) by induction (xn) is increasing. It can be observed again by induction that xn ≤ 2.
Given x1 = √2.
Xn+1 = √2xn.
Let Xn = ℓ
Xn = ℓ
then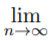 Xn +1 =
Xn +1 = 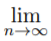 √2xn
√2xn
⇒ ℓ = √2ℓ
⇒ ℓ2 = 2ℓ
⇒ ℓ2 - 2ℓ = 0
⇒ ℓ (ℓ - 2) = o
⇒ ℓ = 0, 2
Since ℓ > 0
∴ ℓ = 2
|
98 videos|34 docs|32 tests
|
FAQs on Sequences of Real Numbers- I - Mathematics for Competitive Exams
| 1. What is the range of a sequence? |  |
| 2. What does it mean for a sequence to be bounded and monotone? |  |
| 3. What is the limit point of a sequence? |  |
| 4. What does the Bolzano-Weierstrass Theorem state? |  |
| 5. What is the difference between a convergent and a divergent sequence? |  |






















