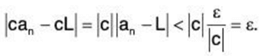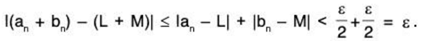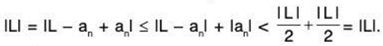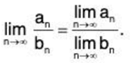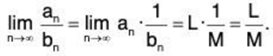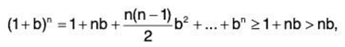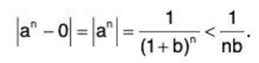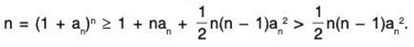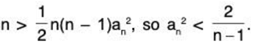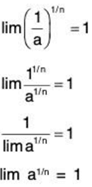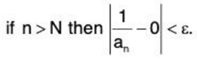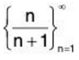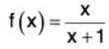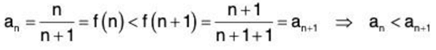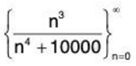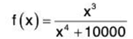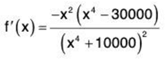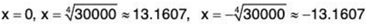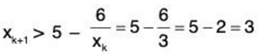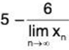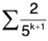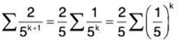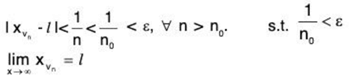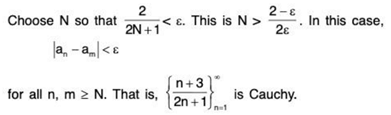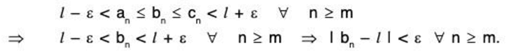Sequences of Real Numbers- II | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| The Algebra of Convergent Sequences |

|
| Lemma, (limits preserve inequalities) |

|
| Subsequence |

|
| Conversely |

|
| Observation |

|
| Cauchy Sequence |

|
| Some important theorems on limits |

|
The Algebra of Convergent Sequences
Theorem. If the sequence {an} converges to L and c ∈ R, then the sequence {can} converges to cL; i.e., 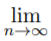 can = c
can = c  an.
an.
Proof. Let’s assume that c ≠ 0, since the result is trivial if c = 0.
Let ε > 0. Since {an} converges to L, we know that there is an n ∈ N so that if n > N.
Thus, for n > N we then have that
which is what we needed to prove.
Theorem. If the sequence {an} converges to L and {bn} converges to M, then the sequence {an + bn} converges to L + M; i.e.,(an + bn) =
an +
bn.
Proof. Let ε > 0. We need to find an N e R so that if n > N
l(an + bn) - (L + M)| < ε.
Since {an} and {bn} are convergent, for the given ε there are integers N1, N2 ∈ N so that
If n > N1 then lan - L| < ε/2 and if n > N2 then lbn - M| < ε/2 Thus, if n > max {N1, N2} then
Theorem. If the sequence {an} converges to L and {bn} converges to M, then the sequence {an • bn} converges to L • M; i.e.,{an • bn} =
an •
bn.
The trick with the inequalities here is to look at the inequality
|anbn - LM| = |anbn - anM + anM - LM|
< |anbn - anMl + lanM - LM|
= lanllbn - M| + |M||an - L|.
So for large values of n, lbn - M| and |an - L| are small and |M| is constant. Now, by Theorem shows that lanI is bounded, so that we will be able to show that lanbn - LMI is small.
Lemma, (limits preserve inequalities)
If the sequence {an} converges to L and {bn} converges to M and if an < bn for all n ≥ m, then L ≤ M.
Proof. Consider the sequence {cn} defined by cn := bn - an.
The Sum Rule for Limits grants that cn → M - L as n → ∞.
Furthermore, the assumption that an = yn for all n ∈ N means that cn ≥ 0 for all n ∈ N.
Applying the main result to the sequence {cn} leads to the conclusion that M-L ≥ 0. That is, L ≤ M.
OR
Let if possible L > M.
Since lim an = L, therefore for ε = (L-M)/2, there exists n1 such that Ian — L| < (L-M)/2 for all n ≥ n1
i.e.. L - (L-M)/2 < an < L + (L-M)/2 for all n ≥ n1
i.e. (L+M)/2 < an < (3L-M)/2 for all n ≥ n1
Similarly, for bn, there exists n2 such that Ibn - M | < (L-M)/2 for all n ≥ n2
i.e. M - (L-M)/2 < bn < M + (L-M)/2 for all n ≥ n2
i.e. (-L+3M)/2 < bn < (L+M)/2 for all n ≥ n2
Let N = max (n1, n2)
Then, for all n ≥ N, bn < (L+M)/2 < an
Let M = max (N, m)
For all n ≥ M, bn < an, a contradiction
Hence L ≤ M.
Lemma. If the sequence {an} converges to L, if an ≠ 0 for all n ∈ N, and if L ≠ 0, then glb{lanl In ∈ N} > 0.
Proof. Let ε = 1/2 ILI > 0. Since {an} converges to L, there is an N ∈ N so that if n > N then lan - L| < |L|/2.
Now if n > N we must have that lanl > I Ll/2. If not then the triangle inequality would imply
Now we set
Then clearly m > 0 and lanl > m for all n ∈ N.
Theorem. If the sequence {an} converges to L, if an ≠ 0 for all n ∈ N, and if L ≠ 0, then the sequence {1/an} converges to 1/L; i.e., 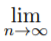 1/an = 1/
1/an = 1/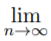 an.
an.
Proof. Let ε > 0. By Lemma there is a n, m > 0 such that lanl > m for all n. Since {an} is convergent there is an integer N ∈ N so that if n > N IL — anl < ε • m|L|.
Then for n > N
Theorem. Suppose that the sequence {bn} converges to M and if {an} converges to L. If bn ≠ 0 for all n ∈ N, and if M ≠ 0, then the sequence {an/bn} converges to L/M; i.e.,
Proof. We use two of the previous theorem to prove this. By Theorem {1/bn} converges to 1/M, so
Theorem: Let {an} be a sequence converging to a then the sequence {lanl} converges to lal:
Proof: This one, we break into three cases.
If a > 0, then (applying the definition of limn→∞ an = a with ε = a) there exists Mo so that an > 0
for n > Mo. In this case, we have lanl = an for n > Mo and lal = a, and so llanl - |a|| = |an - a|. Since there is M1 so that lan - a| < ε for n > M1 we have that llanl - |a|| < ε for n > M = max(Mo, M1), and so limn→∞ lanI = lal.
If a < 0, then (applying the definition of limn→∞ an = a with ε = lal) there exists Mo so that an < 0 for n > Mo. In this case, we have lanl = - an for n > Mo and lal = - a, and so ||anl - |a|| = |-an + al = lan - a|. Since there is M1 so that lan - a| < ε for n > M1, we have that llanl - |a|| < ε for n > M = max(Mo, M1), and so limn→∞ lanl = lal.
If a = 0, then the definition of limn→∞ an = a becomes : for every ε > 0, there exists M so that lan - 0| = |anI < ε for n > M. Since llanll = lanI, we have that the definition of limn→∞ = 0 is satisfied without any further work.
Example 1: Let p > 0 then limn→∞ 1/np = 0.
Sol: Let ε > 0 and let N = (1/ε)1/p. Then n > N implies that np > 1/ε and hence ε > 1/np. Since 1/np > 0, this shows that n > N implies |1/np - 0| < ε.
Example 2: Let lal < 1, then limn→∞ an = 0.
Sol: Suppose a ≠ 0, because lim an = 0 is clear for a = 0. Since lal < 1, we can write
lal = 1/1+|b| where b > 0. By the binomial theorem
so
Now consider ε > 0 and let N = 1/εb.
Then if n > N, we have n > 1/εb and hence lan - 0| < 1/nb < ε.
Example 3: 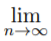 (n1/n) =1.
(n1/n) =1.
Sol: Let an = (n1/n) - 1 and note that an ≥ 0 for all n.
By Theorem it is sufficient for us to show that limn→∞ an = 0.
Since 1 + an = n1/n, we have n = (1 + an)n.
For n ≥ 2 the binomial theorem gives us
Thus,
Thus, we have shown that an <for n ≥ 2.
Thus, lim an = 0.
Example 4: 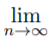 (a1/n) = 1 for a > 0.
(a1/n) = 1 for a > 0.
Sol: Suppose a ≥ 1 then for n ≥ a we have 1 ≤ a1/n ≤ n1/n. Since lim n1/n = 1, it easily follows that lim a1/n = 1. Suppose that 0 < a < 1. Then 1/a > 1 so that lim (1/a)1/n =1.
Thus,
Recall: For a sequence {an} we write lim an = +∞ provided for each M > 0 there is a number N such that n > N implies that an > M.
In this case we will say that {an} diverges to +∞.
We can make a similar definition for lim an = -∞.
Of course, we cannot use the previous theorem when dealing with infinite limits.
Theorem. Let {an} and {bn} be sequence such that lim an = +∞ and lim bn > 0. Then lim anbn = +∞.
Proof. Let M > 0. Choose a real number m so that 0 < m < lim bn. Whether lim b = +∞ or not, there exists N1 so that if n > N1 then bn > m. Since lim an = +∞ there is an N2 so that if n > N2 then
an > M/m.
Setting N = max{N1, N2} means that for n > N, anbn > M/m · m = M.
Theorem. For a sequence {an} of positive real numbers lim an = +∞ if and only if lim 1/an = 0.
Proof. Let {an} be a sequence of positive numbers. We need to show
If lim an = +∞ then lim 1/an = 0 (1)
and If lim 1/an = 0 then then lim an = +∞. (2)
To prove (1) we will suppose that lim an = +∞. Let ε > 0 and let M = 1/ε. Since {an} diverges to +∞, there is an N so that if n > N then an > M = 1/ε. Therefore, if N > n then ε - 1/an > 0, so
Thus, this proves lim 1/an = 0.
To prove (2) suppose that lim 1/an = 0 and let M > 0. Let ε = 1/M. Then since ε > 0 there is an N so that if n > N then. Since an > 0 we then know that
and hence
if n > N then an > M.
This means that lim an = +∞ and 2 holds.
Theorem. A monotonic sequence of real numbers {xn} converges if and only if it is bounded.
Proof: We already know that a convergent sequence is bounded. Hence we just need to show that a monotone and bounded sequence of real numbers is convergent.
Suppose {xn} is a bounded increasing sequence.
Let S denote the non-empty bounded set {xn : n ∈ N}
By the completeness axiom S has a least upper bound, and we let x = sup S.
We claim that lim xn = x. Given any ε > 0, x - ε is not an upper bound for S.
Thus there exists an integer N such that xN > x - ε.
Furthermore, since {xn} is increasing and x is an upper bound for S we have
x - ε < xN ≤ xn ≤ x < x + ε
or equivalently
lxn - x| < ε
for all n ≥ N. Hence lim xn = n.
In the case when the sequence is decreasing, let x = inf S and proceed in a similar manner.
Lemma (On nested intervals). Let the sequence of the intervals {[an, bn]} be such that [an+1, bn+1] ⊂ [an, bn] ∀n ∈ N (such intervals are called nested), and their lengths converge to zero, i.e., 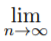 (bn - an) = 0. Then there exists a unique point ξ that belongs to every interval, i.e., ξ ∈ [an, bn] ∀n ∈ N, and ξ
(bn - an) = 0. Then there exists a unique point ξ that belongs to every interval, i.e., ξ ∈ [an, bn] ∀n ∈ N, and ξ 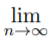 an = sup{an} =
an = sup{an} = 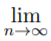 bn = inf{bn}.
bn = inf{bn}.
Proof. The sequence {an} and {bn} are monotonic and bounded:
a1 ≤ an ≤ an+1 ≤ bn+1 ≤ bn ≤ b1 ∀n ∈ N.
By Theorem, they are convergent, andan = sup {an} = a,
bn = inf {bn} = b.
However,(bn - an) = 0 implies that a = b = ξ: and clearly
an ≤ a = ξ = b ≤ bn ∀ n ∈ N.
Next we show that there is no point other than ξ that belongs to all the intervals [an, bn]. Assume the opposite: ∃η ∈ [an, bn] ∀n and η ≠ ξ. Then by Theorem
bn - an ≥ |ξ - n| >0 ∀n ⇒(bn - an ≥ |ξ - η| > 0.
This contradiction completes the proof of the lemma.
Example 5: Determine if the following sequences are monotonic and/or bounded.
(a) {-n2}∞n =0
(b) {(-1)n+1}∞n=1
(c) {2/n2}∞n=5
Sol:
(a) {-n2}∞n = 0
This sequence is a decreasing sequence (and hence monotonic) because, - n2 > - (n + 1)2 for every n.
Also, since the sequence terms will be either zero or negative this sequence is bounded above. We can use any positive number or zero as the bound, M, however, it’s standard to choose the smallest possible bound if we can and it’s a nice number. So, we’ll choose M = 0 since, - n2 ≤ 0 for every n
This sequence is not bounded below however since we can always get below any potential bound by taking n large enough. Therefore, while the sequence is bounded above it is not bounded below. we can also note that this sequence diverges (to -∞).
(b) {(-1)n+1}∞n = 1
The sequence terms in this sequence alternate between 1 and -1 and so the sequence is neither an increasing sequence or a decreasing sequence. Since the sequence is neither an increasing nor decreasing sequence it is not a monotonic sequence. It is an oscillatory sequence. The sequence is bounded however since it is bounded above by 1 and bounded below by -1.
Again, we can note that this sequence is not divergent, it is oscillatory.
(c) {2/n2}∞n = 5
This sequence is a decreasing sequence (and hence monotonic) since,
The terms in this sequence are all positive and so it is bounded below by zero. Also, since the sequence is a decreasing sequence the first sequence term will be the largest and so we can see that the sequence will also be bounded above by 2/25. Therefore, this sequence is bounded.
We can also take a quick limit and note that this sequence converges and its limit is zero.
Example 6: Determine if the following sequences are monotonic and/or bounded.
(a) 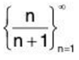
(b) 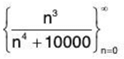
Sol:
(a)
We'll start with the bounded part of this example first and then come back and deal with the increasing/decreasing.
First, n is positive and so the sequence terms are all positive. The sequence is therefore bounded below by zero. Likewise each sequence term is the quotient of a number divided by a larger number and so is guaranteed to be less than one. The sequence is then bounded above by one. So, this sequence is bounded.
Now let’s think about the monotonic question. First, we will often make the mistake of assuming that because the denominator is larger the quotient must be decreasing. This will not always be the case and in this case we would be wrong. This sequence is increasing.
To determine the increasing/decreasing nature of this sequence we will need to calculate I technique. First consider the following function and its derivative.
We can see that the first derivative is always positive and so from calculation we know that the function must then be an increasing function. Notice that,
Therefore because n < n + 1 and f(n) is increasing we can also say that,
In other words, the sequence must be increasing.
Note that now that we know the sequence is an increasing sequence we can get a better lower bound for the sequence. Since the sequence is increasing the first term in the sequence must be the smallest term and so since we are starting at n = 1 we could also use a lower bound of 1/2 for this sequence. It is important to remember that any number that is always less than or equal to all the sequence terms can be a lower bound.
(b)
This is a messy looking
Now, let’s move on to the increasing/decreasing part. As with the problem, many of us will look at the exponents in the numerator and denominator and determine based on that sequence terms must decrease.
This however, isn’t a decreasing sequence. Let’s take a look at the first few terms to see this.
The first 10 terms of this sequence are all increasing and so clearly the sequence can’t be a decreasing sequence. Recall that a sequence can only be decreasing if ALL the terms are decreasing.
Now, we can’t make another common mistake and assume that because the first few terms increase then whole sequence must also increase. If we did that we would also be mistaken as this is also not an increasing sequence.
This sequence is neither decreasing or increasing. The only sure way to see this is to do the Calculus approach to increasing/decreasing functions.
In this case we’ll need to the following function and its derivative.
This function will have the following three critical points,
Remember these are the only points where the function may change sign! Our sequence starts at n = 0 and so we can ignore the third one since it lies outside the values of n that we’re considering. By plugging in some test values of x we can quickly determine that the derivative is positive for 0 < x < ∜30000 ≈ 13.16 and so the function is increasing in this range. Likewise, we can see that the derivative is negative for x > ∜30000 ≈ 13.16 and so the function will be decreasing in this range.
So, our sequence will be increasing for 0 ≤ n ≤ 13 and decreasing for n ≥ 13. Therefore the function is not monotonic.
Finally, note that this sequence will also converge and has a limit of zero.
Example 7: Let x1 = 6 and xn+1 = 5 - 6/xn for all n ∈ N then the sequence converges to.
Sol: x1 = 6
Let xk > 3 for some k ∈ N
then
We have x1 > 3 and if we assume that xk > 3 for some k ∈ N, then xk+1 > 5 - 2 = 3. Hence by the principle of mathematical induction, xn > 3 for all n ∈ N. Therefore (xn) is bounded below. Again, x2
= 4 < x1 and if we assume that xk+1 < xk. for some k ∈ N, then XK+2 - Xk+1 = 6 (1/xk - 1/xk+1) < 0 ⇒ xk+2 < xk+1. Hence by the principle of mathematical induction, xk+l < xn for all n ∈ N. Therefore (xn) is decreasing.
<xn> is bounded and monotonic. Hence <xn> is convergent. Let ℓ =Xn. Then
xn+1
⇒ ℓ = 5 - 6/ℓ (since xn > 3 for all n ∈ N, ℓ ≠ 0) ⇒ (ℓ - 2)(ℓ - 3) = 0 ⇒ ℓ = 2 or ℓ = 3. But xn > 3 for all n ∈ N, so ℓ ≥ 3. Therefore ℓ = 3.
Example 8: The series 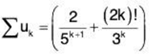 converges or diverges
converges or diverges
Sol: The given series is a sum of two series. We will look at each of them separately and hope that the two results can be put together. First consider the series
This is a series that can be converted to a geometric series.
Since q = 1/5 satisfies Iql < 1, this series converges.
Now we will look at the series
When we see factorial, we immediately think of the Ratio test.
Since λ > 1, this series diverges.
Since the given series is the sum of a convergent and a divergent series, it is divergent.
Subsequence
Let <an> be any sequence. Let <n1, n2, ...., nk ...) be a sequence of positive integers such that i > j ⇒ ni > nj Then the sequence (an1,an2,...., ank....}, written as (ank), is called a subsequence of (an).
Let {aj}∞j=1 be a sequence. When we extract from this sequence only certain elements and drop the remaining ones we obtain a new sequences consisting of an infinite subset of the original sequence.
That sequence is called a subsequence and denoted by {ajk}∞k=1
<a10, a11, a12, ...) is a subsequence of <an>.
Theorem: If sequence bdd., then every subsequence is bdd and conversely.
Proof. Let {an} be any bdd. sequence
then ∃ m, M ∈ R such that
m ≤ an < M ∀ n ∈ N ...(1)
Let {ank} be any subsequence of {an}
⇒ m ≤ ank ≤ m (from (1)) ∀ nk ∈ N
∴ {ank} is also bdd subsequence
Conversely
Let every subsequence of {an} be bdd.
As every sequence is a subsequence of itself.
∴ {an} is bdd.
Note: If we have to show {an} is unbounded.
Then show ∃ a subsequence of {an} which is unbounded.
Ex.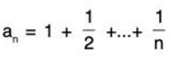
Consider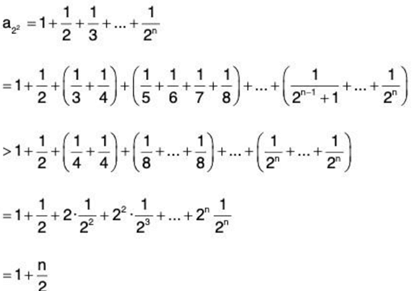
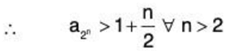
So, {a2n} is unbounded
Hence, {an} is unbounded
Observation
(i) A sequence has a constant subsequence iff ∃ a real no. which appears in the sequence infinite many times.
(ii) If range of a sequence is a finite set then there exist a real no. which appears in the sequence infinite many times.
Theorem: If a sequence <an> converges to I, then every subsequence of <an> converges to I.
Proof: Let <an> be a subsequence of <an>.
Since an → I, therefore, for any ε > 0, there exists a positive integer m such that
lan - II < ε ∀ n ≥ m.
In particular, |ank — I|< ε ∀ nk ≥ m.
Hence (ank} converges to I.
Theorem: Every bounded sequence has a convergent subsequence.
Proof: Let <xn> is bounded
Case 1: When the range of the sequence is finite.
If the range of <xn> in finite then at least one element ‘a’ repeats infinitely because a sequence has infinite number of terms, if we choose this element ‘a’ again and again then the subsequence <a, a, ...> formed is convergent.
Case 2: When the range of the sequence is infinite
<xn> is bounded and range is infinite bounded subset of set of real no. R we know that set of bounded real no. has at least one limit point. Therefore, let I is the limit point of <xn>.
For each n ∈ N, ∃ vn ∈ N s.t.
Let < xV1, xV2,...xVn,...> be a subsequence of <xn>.
∴ for given ε > 0 ∃ no t ∈ N s.t. 1/no < ε
then
⇒ < xv1, xv2, ... xvn, ... > is convergent.
Theorem: If the subsequences {a2n-1} and {a2n} of a sequence {an} converge to the same limit I, then the sequence {an} converges to I.
Proof. Let ε > 0 be given
{a2n-1} converges to I
⇒ For ε > 0, ∃ a positive integer m1 such that la2n-1 - II < ε ∀ n ≥ m1
{a2n-1} converges to I
⇒ For ε > 0, ∃ a positive integer m2 such that la2n - II < ε ∀ n ≥ m2
Let m = max. {m1, m2}, then la2n-1 - Il < ε and la2n - II < ε ∀ n ≥ m
⇒ lan — II < ε ∀ n ≥ m
⇒ {an} converges to I.
Cauchy Sequence
A sequence <an> of real numbers is said to be a Cauchy sequence if for every ε > 0 there exists a natural number N such that for all natural numbers n, m > N, the terms an, am satisfy lan - aml < ε. A sequence <an> is said to be a Cauchy sequence if for any ε > 0, there exists a positive integer m such that lan - aml < ε, whenever n ≥ m.
Theorem: Cauchy Sequence is bounded.
Proof: Let <an> be a Cauchy sequence.
For ε = 1, there exists a positive integer m such that
lan - amI < 1, whenever n ≥ m,
or am - 1 < an < am + 1, whenever n ≥ m.
Let k = min {a1, a2, ...., am-1, am - 1},
K = max {a1, a2,...., am-1, am + 1}.
Then k ≤ an ≤ K for all n.
Hence <an> is bounded.
Theorem: If a subsequence of a Cauchy sequence converges to I, then the sequence also converges to I.
Proof: Let < xn> be a cauchy sequence, then by definition for any ε > 0 ∃ no s.t.
lxm- xnl < ε/2 ∀ m, n > 0 ...(1)
Let < xvn> be the subsequence of < xn> and lim xvn = I, then for I > 0 ∃ no ∈ N s.t.
|xn — II < ε/2 ∀ vn > no ...(2)
Now |xn - II = lxnIl ≤ | xVn - xn| + |xVn - I|
< ε/2 + ε/2 ∀ n > vn [by (1) and (2)]
⇒ |xn - II < ε ∀n > vn
⇒ lim xn= I
Theorem: A sequence X = <xn> in R is convergent if and only if it’s Cauchy.
Proof: "⇒"
If x := lim X, then given ∈ > 0 there is a natural number K such that if n ≥ K then IXn - x I < ∈/2. Thus, if n, m ≥ K, then we have lxn - xmI = I (xn - x) + (x - xm) I ≤ lxn - x I + lxm - x I < ∈/2 + ∈/2 = ∈-Since ∈ > 0 is arbitrary, it follows that <xn> is a Cauchy sequence.
(Here we used the first definition)
“ ⇐ ” let X = (xn) be a Cauchy sequence; we will show that X is convergent to some real number. First we observe that the sequence X is bounded. Therefore, by the Bolzano-Weierstrass Theorem, there is a subsequence X ’ = < xnλ> of X that converges to some real number X*. We shall complete the proof by showing that X converges to X*.
Since X = (xn) is a Cauchy sequence, given > 0 there is a natural number N such that if n, m N then lxn -xml<.
Since the subsequence X’ = () converges to x*, there is a natural number K>N belonging to the set {n1, n2, ...} such that |xk - x*| <.
Thus nN,lxn-xKl < lxn-x*llxn -xKl + lxK- x*l <.
Hence, X converges to x*.
Theorem : (Cauchy’s Principle of Convergence)
A necessary and sufficient condition for a series ∑un to converge is that to each ε > 0, there exists a positive integer m, such that |Sn - Sm| < ε
lum+1 + um+2+ ... + unI < ε, for all n ≥ m.
Proof: Let <Sn> be the sequence of partial sums of the series ∑un. By definition, ∑un converges ⇔ <Sn> converges
⇔ To each ε > 0, there exists a positive integer m such that
ISn - Sml < ε ∀ n ≥ m
(Cauchy's Principle of Convergence for Sequences)
⇔ I (u1 + u2 + ... + um + um+1, + um+2, + ... + un) - (u1 + u2 + ... + um)] < ε ∀ n ≥ m
⇔ |um+1, + um+2 + .... + un | < ε ∀ n ≥ m.
Hence the theorem.
Example 1: (a) Show that if {an}∞n=1 is Cauchy then {an2}∞n=1 is also Cauchy.
(b) Given an example of a Cauchy sequence {an2}∞n=1 such that {an}∞n=1 is not Cauchy.
Sol: (a) Since {an}∞n=1 is Cauchy, it is convergent. Since the product of two convergent sequences is convergent the sequence {an2}∞n=1 is convergent and therefore is Cauchy.
(b) Let an = (-1)n for all n ∈ N. The sequence {an}∞n=1 is not Cauchy since it is divergent. However, the sequence {an2}∞n=1 = {1, 1, ....} converges to 1 so it is Cauchy.
Example 2: Let {an}∞n=1 be a Cauchy sequence such that an is an integer for all n ∈ N. Show that there is a positive integer N such that an = C for all n ≥ N, where C is a constant.
Sol: Let ε = 1/2. Since {an}∞n=1 is Cauchy, there is a positive integer N such that if m, n > N we have |am - an| < 1/2. But am - an is an integer so we must have an = aN for all n ≥ N.
Example 3: What does it mean for a sequence {an}∞n=1 to not be Cauchy?
Sol: A sequence {an}∞n=1 is not a Cauchy sequence if there is a real number ε > 0 such that for all positive integers N there exist n, m ∈ N such that n, m ≥ N and lan - am| < ε.
Example 4: Let {an}∞n=1 and {bn}∞n=1 be two Cauchy sequences. Define cn = lan - bnl. Show that {cn}∞n=1 is a Cauchy sequence.
Sol: Let ε > 0 be given. There exist positive integers N1 and N2 such that if n, m ≥ N1 and n, m ≥ N2 we have lan - amI < ε/2 and lbn - bml < ε/2. Let N = N1 + N2. If n, m ≥ N then lcn - cml = |lan - bn| — lam - bmI ≤ l(an - bn) + (am - bm)l ≤ lan - amI + lbn - bmI < ε. Hence {cn}∞n=1 is a Cauchy sequence.
Example 5: Explain why the sequence defined by an = (- 1)n is not a Cauchy sequence.
Sol: We know that every Cauchy sequence is convergent. We also know that the given sequence is divergent. Thus, it can not be Cauchy.
Example 6: Every subsequence of a Cauchy sequence is itself a Cauchy sequence.
Sol: For a sequence (sn)n∈N, a subsequence is a sequence of the form (snk)k∈N for a strictly increasing sequence of natural numbers 1 ≤ n1 < n2 < n3 < ..... For every integer k ∈ N, by induction on k, nk is at least as large as k.
First, let (sn)n∈N, be a sequence that converges to s. Let (snk)k∈N be a subsequence. For every ε > 0, since (sn)n∈N, converges, there exists N ∈ N such that for every n ∈ N with n ≥ N, |sn - s| is less than ε. For every k ∈ N with k ≥ N, since nk is at least as large as k, in particular nk = N. Therefore, |snk -s| is less than ε. Thus (snk)k∈N converges to s.
Next, let (snk)k∈N be a Cauchy sequence. For every ε > 0, there exists N ∈ N such that for every m, n ∈ N with m ≥ N and with n ≥ N, |sn - sm| is less than ε. For every k, I ∈ N with k ≥ N and with I ≥ N, then nk ≥ k ≥ N and ni > I > N. Therefore, |Snk - Sni| is less than ε. Thus (snk)k∈N is a Cauchy sequence.
Example 7: Prove directly from the definition that the sequence 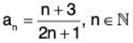 is a Cauchy sequence.
is a Cauchy sequence.
Sol: Let ε > 0 be given. Let N be a positive integer to be chosen. Suppose that n, m ≥ N. We have
Example 8: Consider a sequence defined recursively by a1 = 1 and an+1 = an + (-1 )n n3 for all n ∈ N. Show that such a sequence is not a Cauchy sequence. Does this sequence converge?
Sol: We will show that there is an ε > 0 such that for all N ∈ N there exist m and n such that m, n ≥ N but lam - anl > ε. Note that lan+1 - anI = n3 ≥ 1. Let N ∈ N. Choose m = N + 1 and n = N. In this case, lam - anl = N3 ≥ 1 = ε. Hence, the given sequence is not a Cauchy sequence. Since every convergent sequence must be Cauchy, the given sequence is divergent.
Some important theorems on limits
Theorem : If an ≥ 0 ∀ n ∈ N and 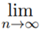 an = I, then I ≥ 0.
an = I, then I ≥ 0.
Proof: Let, if possible, I < 0.
Let ε = —I > 0.
Sincean = I, so there exists a positive integer m such that
|an — I| < — I ∀ n ≥ m
⇒ an - I ≤ |an - I| < — I ⇒ an < — I + I = 0 ∀ n ≥ m
⇒ an < 0 ∀ n ≥ m,
which contradicts the fact that an ≥ 0 ∀ n. Hence I ≥ 0
Theorem: If <an> and <bn> be two sequences such that an ≤ bn ∀ n ∈ N, then lim an ≤ lim bn
Proof: We see that an ≤ bn ⇒ bn ≥ an ⇒ bn - an ≥ 0
⇒(bn - an) ≥ 0,
⇒bn -
an ≥ 0 ⇒
bn ≥
an.
Hencean ≤
bn.
Theorem : (Sandwich Theorem)
If <an>, <bn> and <cn> be three sequences such that
(i) an ≤ bn ≤ cn ∀ n ∈ N,
(ii) 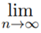 an = I =
an = I = 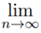 cn
cn
then 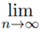 bn = I.
bn = I.
Proof: Let ε > 0 be given.
Sincebn = I, there exists a positive integer m1 such that
Sincecn = I, there exists a positive integer m. such that
Let m = max {m1, m2}. Then
I - ε < an < I + ε and I - ε < cn < I + ε, ∀ n ≥ m. (*)
From (*) and condition (i), we obtain
Hencebn =I.
Theorem : Ratio test for convergence of sequence
If <an> be a sequence of positive number such that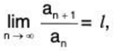
- If I < 1, then
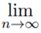 (an) = 0
(an) = 0 - If I < 1, then
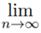 (an) = ∞
(an) = ∞ - If I = 1, then Test fails.
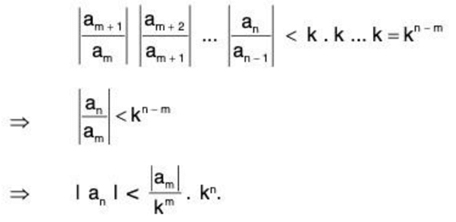
Proof: (1) Since I I I < 1, we can choose a positive number ε so small such that
I I I + ε + 1 or k < 1. where k = I I I + ε.
Sincethere exists a positive integer m such that
Putting n = m, m + 1, ... , (n - 1) successively and multiplying, we get
We know kn → 0 as n → ∞, since 0 < k < 1.
Using in (2), we see that IanI → 0 as n → ∞. Hence lim an = 0.
|
98 videos|34 docs|32 tests
|
FAQs on Sequences of Real Numbers- II - Mathematics for Competitive Exams
| 1. What is a subsequence in the context of convergent sequences? |  |
| 2. How is a Cauchy sequence defined in the study of convergent sequences? |  |
| 3. Can you provide an example of a convergent sequence? |  |
| 4. Are all convergent sequences Cauchy sequences? |  |
| 5. How can the algebraic properties of convergent sequences be used in mathematical proofs? |  |