Series of Real Numbers- I | Mathematics for Competitive Exams PDF Download
Introduction (Series of Real Numbers)
A finite series is given by the terms of a finite sequence, added together. For example, we could take the finite sequence
(2k + 1)10k=1
Then the corresponding example of a finite series would be given by all of these terms added together,
3 + 5 + 7 + .... + 21
We can write this sum more concisely using sigma notation. We write the capital Greek letter sigma, and then the rule for the kth term. Below the sigma we write ‘k = V . Above the sigma we write the value of k for the last term in the sum, which in this case is 10. So in this case we would have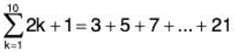
and in this case the sum of the series is equal to 120
In the easy way, an infinite series is the sum of the terms of an infinite sequence. An example of an infinite sequence is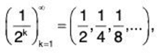
And then the series obtained from this sequence would be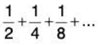
With a sum going on forever. Once again we can use sigma notation to express this series. We write down the sigma sign and the rule for the k-th term. But now we put the symbol for infinity above the sigma, to show that we are adding up an infinite number of terms. In this case we would have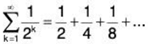
Key points: A finite series is given by all the terms of a finite sequence, added together.
A infinite series is given by all the terms of an infinite sequence, added together.
Definition
An expression of the form a1 + a2 + a3 + ... + an + ... where each an is a real number, is called an infinite series of real numbers and is denoted by 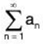 an or ∑ an.an is called the nth term of the series ∑ an.
an or ∑ an.an is called the nth term of the series ∑ an.
Example 1: 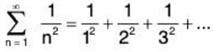
Example 2: 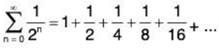 is a n infinite series- The sequence of partial sums looks like:
is a n infinite series- The sequence of partial sums looks like: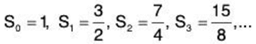
We saw above that this sequence converges to 2, so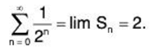
Example 3: The number n!, read n factorial, is defined as the product of the first n positive integers;
n! = 1 - 2 ..... n
<n!> is an important sequence. Its first few terms are
1, 2, 6, 24, 120, 720, ...
By convention, 0! is defined by 0! = 1.
- 1 + 1 + 1 + 1 + 1 + 1 + .... =
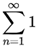
- 1 + 1/2 + 1/3 + 1/4 + .... =
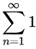 1/n
1/n - 1/2 + 1/4 + 1/8 + ... =
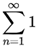 1/2n
1/2n - 1 + 1/4 + 1/9 + 1/16 + ... =
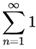 1/n2
1/n2 - 1- 1 + 1- 1 + 1 - 1 + ... =
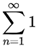 (-1)n
(-1)n 
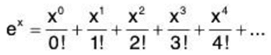
Sequence of Partial Sums of Series
Recall : A sequence {an} is a function which assigns a real number an to each natural number n : 1, 2, 3, 4, 5......i.e., a sequence is an ordered list of real numbers : a1, a2, a3, a4, a5, ...,
Example 1:  generates the sequence
generates the sequence 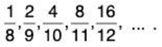
Definition: An infinite series  an is the sum of the numbers in the sequence {an}, i.e.,
an is the sum of the numbers in the sequence {an}, i.e.,  an = a1 + a2 + a3 + a4 + a5 + ... .
an = a1 + a2 + a3 + a4 + a5 + ... .
Example 2: 
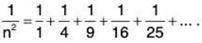
We need a more precise definition of an infinite series 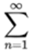 an. Begin by constructing a new sequence of partial sums by letting (This step by step by step process will be called the Sequence of Partial Sums Test for the infinite series
an. Begin by constructing a new sequence of partial sums by letting (This step by step by step process will be called the Sequence of Partial Sums Test for the infinite series 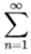 an.)
an.)
S1 = a1,
S2 = a1 + a2,
S3 = a1 + a2 + a3,
S4 = a1 + a2 + a3 + a4,
Sn = a1 + a2 + a3 + a4 + ... + an.
We can now say that the value of the infinite series is precisely the value of the limit of its sequence of partial sums, i.e., an = a1 + a2 + a3 + a4 + ....
an = a1 + a2 + a3 + a4 + ....
=  (a1 + a2 + a3 + a4 + ... + an)
(a1 + a2 + a3 + a4 + ... + an)
= 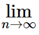 Sn.
Sn.
Examples of Partial Sums
For the sequence 1, 1, 1, 1,..., we have 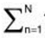 1 = N → ∞. Thus,
1 = N → ∞. Thus, 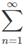 is divergent.
is divergent.
For the sequence 1, -1, 1, -1,..., we have S1 = 1, S2 = 0, S3 = 1, etc. In general , SN = 1 for N odd and SN = 0 for N even. Thus,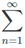 (-1)n is oscillatory.
(-1)n is oscillatory.
The Harmonic Series
If one computes the partial sums for 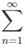 1/n one finds S1 = 1, S2 = 3/2 = 1.5, S3 = 11/6 ≈ 1.87, S10 ≈ 2/93, S20 ≈ 3.40, S1000 ≈ 7.49, S100,000 ≈ 12.09. If fact, SN → ∞ So that
1/n one finds S1 = 1, S2 = 3/2 = 1.5, S3 = 11/6 ≈ 1.87, S10 ≈ 2/93, S20 ≈ 3.40, S1000 ≈ 7.49, S100,000 ≈ 12.09. If fact, SN → ∞ So that 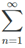 1/n diverges.
1/n diverges.
If one computes the partial sums for 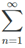 1/n2, then one obtains S1 = 1, S2 = 5/4 = 1.25, S3 = 49/36 ≈ 1.36, S10 ≈ 1.55, S100 ≈ 1.63, S1000 ≈ 1.64.
1/n2, then one obtains S1 = 1, S2 = 5/4 = 1.25, S3 = 49/36 ≈ 1.36, S10 ≈ 1.55, S100 ≈ 1.63, S1000 ≈ 1.64.
In fact,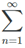 1/n2 = (2) = π2/6 ≈ 1.644934068
1/n2 = (2) = π2/6 ≈ 1.644934068
Definitions
- A series ∑ an is said to be convergent, if the sequence <sn> of partial sums of ∑ an is convergent. If
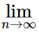 Sn = s, then S is called the sum of the series ∑ an. We write S =
Sn = s, then S is called the sum of the series ∑ an. We write S = 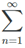 an.
an. - The series ∑ an is said to be divergent, if the sequence <Sn> of partial sums of ∑ an is divergent,.
- The series ∑ an is said to oscillate, if the sequence <Sn> of partial sums of ∑ an oscillates.
Example : (Geometric series) The series 1 + r + r2 + r3 + ... (r > 0) converges if r < 1 and diverges if r > 1.
Convergence of a Geometric Series
a geometric series with ratio r diverges if Irl ≥ 1. If 0 < Irl <1, then the series converges to the sum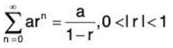
Proof: It is easy to see that the series oscillates if r = ±1. then sn = a + ar +ar2 + .... + arn- 1. multiplication by r yields
rSn = ar + ar2 +... +arn.
Subtracting the second equation from the first produces Sn - rSn = a - ar2. Therefore. Sn (1 - r) = a(1 - rn). and the partial sum is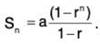
If 0 < Irl < 1, it follows that rn → 0 as n → ∞, and you obtain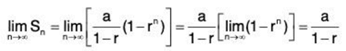
which means that series converges and its sum is a/(1 - r). It is left to you to show that the series diverges if Irl > 1.
Example can be given, such as an = n is an unbounded sequence with no limit point and an = 1, if n is even; an = n, if n is odd is an unbounded sequence with a limit point 1.
Example 1: The series ∑ (- 1)n-1 oscillates.
Example 2: Perform the following index shifts.
(a) Write 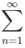 arn-1 as a series that starts at n = 0.
arn-1 as a series that starts at n = 0.
(b) Write 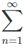
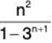 as a series that starts at n = 3.
as a series that starts at n = 3.
Solution:
(a) In this case we need to decrease the initial value by 1 and so the n in the term must increase by 1 as well.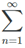 arn-1 =
arn-1 = 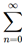 ar(n+1)-1 =
ar(n+1)-1 = 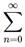 arn
arn
(b) For this problem we want to increase the initial value by 2 and so all the n's in the series terms must decrease by 2.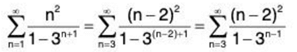
Note: The nature of a series is not affected by the addition, alteration or omission of a finite number of terms or by multiplication of all the terms by a fixed non-zero number.
(a) ∑ (un ± vn) = s ± t
(b) ∑ kun = ks, k ∈ R
Example 3: Convergent and Divergent Geometric Series
(a) The geometric series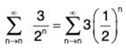
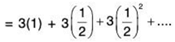
has a ratio of r = 1/2 with a = 3, Because 0 < Irl < 1, the series converges and its sum is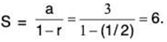
(b) The geometric series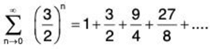
has a ratio of r = 3/2. Because Irl ≥ 1. the series diverge.
Example 4: A Geometric Series for a Repeating Decimal
Use a geometric series to write 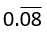 as the ratio of two integers.
as the ratio of two integers.
Solution: For the repeating decimal 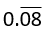 , you can write
, you can write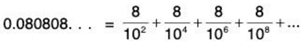

For this series, you have a = 8/102 and r = 1/102. So.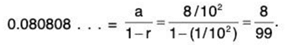
Theorem : Limit of nth Term of a Convergent Series
If 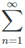 an converges, then
an converges, then 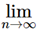 an = 0.
an = 0.
Proof: Assume that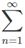 an =
an = 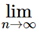 Sn = L
Sn = L
Then, because Sn = Sn-1 + an and 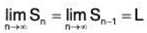
it follows that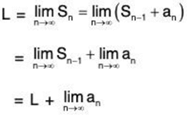
which implies that {an} converges to 0.
Theorem : nth Term Test for Divergence
If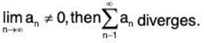
Example 5: Using the nth Term Test for Divergence
(a) For the series 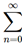 2n. we have
2n. we have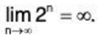
So, the limit of the nth term is not 0 and the series diverges.
(b) For the series  .
.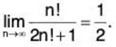
So, the limit of the nth term is not 0 and the series diverges.
(c) For the series  1/n, we have
1/n, we have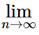 1/n = 0
1/n = 0
Because the limit of the nth term is 0. The nth-Term Test for Divergence does not apply and you can draw no conclusion about convergence or divergence.
Tests of Convergence of Series
Some important comparison series
1. Geometric series
∑un = 1 + r + r2 + r3 + ... + rn-1 + rn + ....
- is convergent, when I r I < 1
- is divergent, when r ≥ 1
- is oscillating finitely, when r = -1
- is oscillating infinitely, when r < -1
2. Hyperharmonic series (or p-series)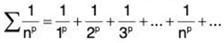
- is convergent when p > 1
- is divergent, when p ≤ 1
3. The Auxiliary Series
The series 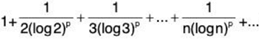 is convergent if p > 1 and divergent if p ≤ 1.
is convergent if p > 1 and divergent if p ≤ 1.
Comparison Test
Test I. First Comparison Test
Let ∑un and ∑vn be two positive term series such that
un ≤ k vn ∀ n ≥ m. ...(1)
(k being a fixed positive number and m a fixed positive integers)
Then
(i) ∑vn converges ⇒ ∑un converges.
(ii) ∑un diverges ⇒ ∑un diverges.
Proof: Let <Sn> and <Tn> be the sequence of partial sums of the series ∑un and ∑vn respectively.
For n ≥ m, we have
Sn - Sm = (u1 + u2 + ... + um + um+1 + um+2 + ... + un) - (u1 + u2 + ... + um)
or Sn - Sm = um+1 + um+2 + ... + un. ... (2)
Similarly,
Tn - Tm = vm+1 + vm+2 + ... + vn. .... (3)
From (1) and (2), we obtain
Sn - Sm ≤ k (vm+1 + vm+2 + ...vn)
or Sn - Sm ≤ k (Tn - Tm) using (3)
or Sn ≤ k Tn +a, ... (4)
where a = Sm - k Tm is a fixed number.
(i) Suppose ∑ vn converges.
The sequence <Tn> of partial sums of ∑vn is bounded above i.e., there exists a positive real number t such that
Tn ≤ t ∀ n. ...(5)
From (4) and (5),
Sn ≤ kt + a ∀ n.
Thus the sequence <Sn> of partial sums of ∑un is bounded above and so ∑un is convergent.
(ii) Suppose ∑un diverges.
Then 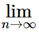 Sn = + ∞ .... (6)
Sn = + ∞ .... (6)
From (4) and (6), we obtain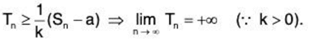
It follows that the sequence <Tn> of partial sums of the series ∑un diverges and so ∑vn diverges.
Example 1: Test for convergence the series:
(i) 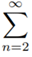 1/logn,
1/logn,
(ii) 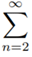 1/n2logn
1/n2logn
Solution: (i) We know log n < n for all n ≥ 2.
∴ 
Since ∑1/n diverges, so by First Comparison Test,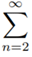 1/log n, diverges.
1/log n, diverges.
(ii) We know 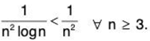
Since ∑1/n converges, so by First Comparison Test, 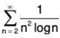 converges
converges
Example 2: Test for the convergence of the series: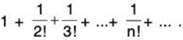
Solution: We that n ! ≥ 2n-1 ∀ n ≥ 2.
∴ 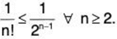
Now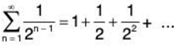 being a geometric series with common ratio 1/2 < 1 is convergent. Hence, by First Comparison Test, ∑1/n! is convergent.
being a geometric series with common ratio 1/2 < 1 is convergent. Hence, by First Comparison Test, ∑1/n! is convergent.
Test II. Second Comparison Test
If ∑un and ∑vn are two positive term series such that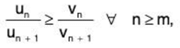 ....(1)
....(1)
Then
(i) ∑vn converges ⇒ ∑un converges,
(ii) ∑un diverges ⇒ ∑vn diverges,
Proof: For n ≥ m, we have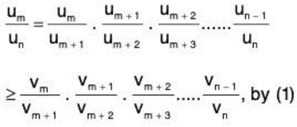
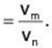
Thus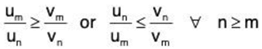
∴ un ≤ k vn ∀ n ≥ m, ....(2)
where k = um/vm is a fixed positive number.
(i) ∑vn converges ⇒ ∑un converges,
(ii) ∑un diverges ⇒ ∑vn diverges.
Test III. Limit Form Test
Let ∑un and ∑vn be two positive term series such that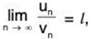 (I is finite and non-zero).
(I is finite and non-zero).
Then ∑un and ∑vn converge or diverge together.
Proof: Since un/vn > 0 for all n, so 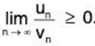
Thus / > 0, as / ≠ 0
Let ε > 0 be some number such that / - ε > 0.
Since 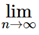 un/vn = /, so there exists a positive integer m such that
un/vn = /, so there exists a positive integer m such that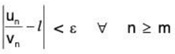
or / - ε < un/vn < / + ε ∀ n ≥ m, where vn > 0 ∀ n.
∴ (/ - ε) vn < un < (/ + ε) vn ∀ n ≥ m. ....(1)
From (1), we consider
un < (/ - ε) vn ∀ n ≥ m. ....(2)
(Here / + ε is a fixed positive number)
Applying First Comparison Test in (2), we obtain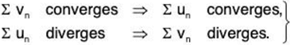 ... (A)
... (A)
From (1), we consider
(/ - ε) vn < un ∀ n ≥ m
or vn < kun ∀ n ≥ m, ....(3)
where k = 1// - ε > 0 is a fixed number.
Applying First Comparison Test in (3), we obtain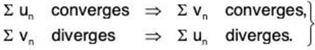 ...(b)
...(b)
From (A) and (B), it follows that
∑un converges ⇔ ∑vn converges,
∑vn diverges ⇔ ∑vn diverges.
Hence the two series ∑un and ∑vn converge or diverge together.
Remark
- In order to apply the Limit form test to a given series ∑un, we have to select a series ∑vn (which is usually a p-series) in which the nth term of vn behaves as un, for large values of n.
Example 3: Test each of the following series for convergence:
(i) 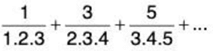
(ii) 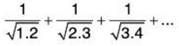
Solution:
(i) 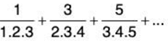
The nth term of this series of 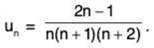

So ∑un and ∑vn converge or diverge together (Limit From Test). Since 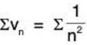 converges, so ∑un converges.
converges, so ∑un converges.
(ii) 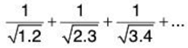
The nth term is 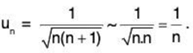
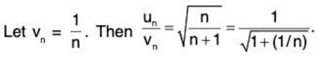
Now  and finite.
and finite.
So ∑un and ∑vn converge or diverge together.
Since ∑vn = ∑1/n diverges, so ∑un diverges.
Example 4: Test for convergence the series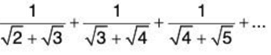
Solution: We have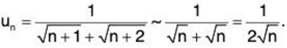
Let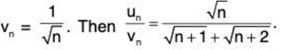
Now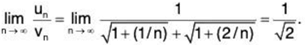
So ∑un and ∑vn converge or diverge together.
Example 5: Test for converges the series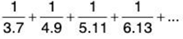
Solution: We have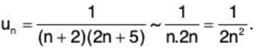
Let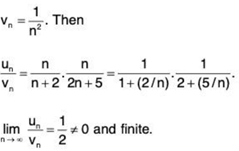
So ∑un and ∑vn converge or diverge together.
Since ∑vn = E 1/n2 converges, so the given series ∑un also converges.
Example 6: Test for convergence the series whose nth term is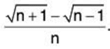
Solution:
or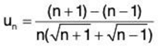
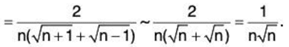
Let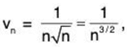 so that ∑vn converges.
so that ∑vn converges.
Now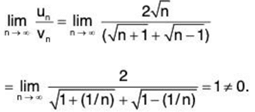
So ∑un and ∑vn converge or diverge together.
Since ∑vn converges, so the given series ∑un also converges.
Example 7: Test for the convergence of the series: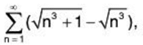
Solution: 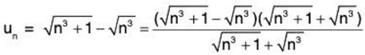
or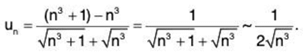
Let
Now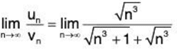
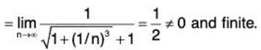
So ∑un and ∑vn converge or diverge together.
Since ∑vn converges, so the given series ∑un converges.
Example 8: Test for the convergence of the series whose n* term is
{(n3 + 1)1/3 - n}.
Solution: Let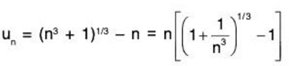
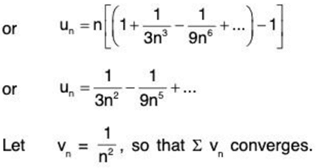
Now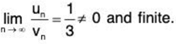
So ∑un and ∑vn converge or diverge together.
Since ∑vn converges, so ∑un converges.
Example 9: Test for convergence the series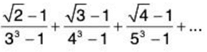
Solution: The nth term of the given series is
Let
So ∑un and ∑vn converge or diverge together.
Since ∑vn = ∑1/n5/2 converges, so the given series converges.
Example 10: Test the convergence of the series S 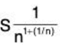 .
.
Solution: We have
Then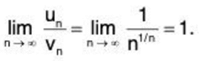
Thus the two series ∑un and ∑vn converge or diverge together. Since ∑vn = ∑1/n diverges, so the given series ∑un diverges.
Example 11: Show that the series 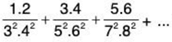 converges.
converges.
Solution: The nth term of the given series is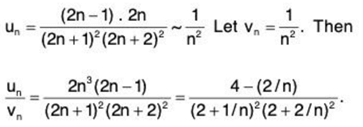
∴ 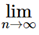 un/vn = 1, so that ∑un and ∑vn converge or diverge together.
un/vn = 1, so that ∑un and ∑vn converge or diverge together.
Since ∑vn = ∑1/n2 converges, so the given series ∑un also converges.
Example 12: Show that the series 1 + a + b + a2 + b2 + a3 + b3 + ..., 0 < a < b < 1 is convergent.
Solution: Since 0 < a < b < 1, an < bn ∀ n ≥ 0.
Since ∑bn is a geometric series with common ratio b, 0 < b < 1 ; ∑bn is convergent. Hence, by First comparison test, the given series ∑un is convergent.
Ratio Test
Test IV. D'Alembert’s Ratio Test
Let ∑un be a positive terms series such that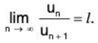 ... (1)
... (1)
Then
(i) ∑un converges if / > 1,
(ii) ∑un diverges if /< 1.
Test fails if / = 1.
Proof. Case I. Let / > 1.
We can choose some ε > 0 such that / - ε > 1 or α > 1, α = / - ε.
Using (1), there exists a positive integer m1 such that
Consider
or ...(2)
...(2)
where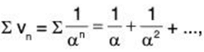 , being a geometric series with common ratio 1/α < 1, is convergent.
, being a geometric series with common ratio 1/α < 1, is convergent.
Hence ∑un is convergent (by Second Comparison Test is applied in (2)).
Case II. Let / < 1.
We can choose another ε > 0 such that / + ε < 1
β < 1, β = / + ε.
Using (1), there exists a positive integer m2 such that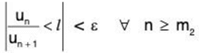
or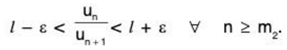
Consider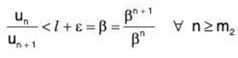
or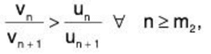 ....(3)
....(3)
where ∑vn = ∑1/βn, being a geometric series with common ratio 1/β > 1, is divergent. Hence, by Second Comparison Test as applied in (3), ∑un is divergent.
Case III. We shall give examples of two series : one convergent and the other divergent but both satisfying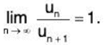
The series ∑un = ∑1/n is divergent, but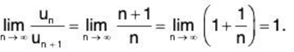
The series ∑un = ∑1/n2 is convergent, but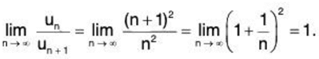
Remark 1: Another equivalent form of Ratio Test is as follows:
If ∑un is a positive term series such that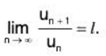 ...(1)
...(1)
Then
(i) ∑un is convergent if / < 1.
(ii) ∑un is divergent if / > 1.
Proof: We have 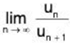 m, where m = 1//.
m, where m = 1//.
Then ∑un converges if m > 1 ⇒ 1// > 1 ⇒ / < 1,
and ∑un converges if m < 1 ⇒ 1// < 1 ⇒ / < 1.
Remark 2 : If ∑un is a positive term series such that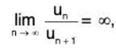 then ∑un is convergent.
then ∑un is convergent.
Proof : It is given that the sequence  diverges to ∞.
diverges to ∞.
So there exists a positive integer m such that
or
where ∑vn = ∑1/2n, being a geometric series with common ratio 1/2 <1, is convergent. Hence, by Second Comparison Test, ∑un is convergent.
Remark 3: If ∑un is a positive term series such that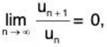 then ∑un is convergent.
then ∑un is convergent.
Proof : For ε = 1/2, there exists a positive integer m such that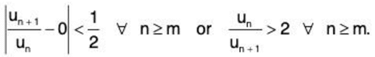
The result now follows by Remark 2.
Example 1: Test for the convergence of the series: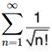
Solution: Let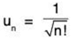
By applying ratio test -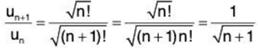
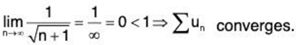
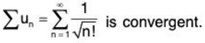
Example 2: Test for convergence the series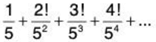
Solution: We have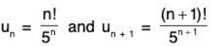
∴ 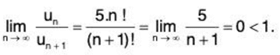
By Ratio Test, the given series diverges.
Example 3: Test for convergence the series
(i) 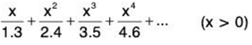
(ii) 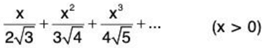
Solution:
(i) 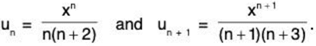
∴ 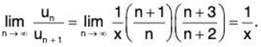
By Ratio Test, ∑un converges of 1/x > 1 i.e., x < 1 and ∑un diverges if 1/x < 1 i.e., x > 1. The test fails for x = 1.
For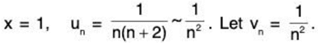
∴ 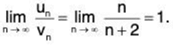
So ∑un and ∑vn converge or diverge together.
Since ∑vn = ∑1/n2 converges, so ∑un converges (for x = 1).
Hence the given series converges for x ≤ 1 and diverges for x > 1.
(ii) We have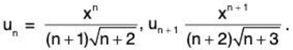
∴ 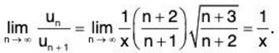
By Ratio Test, the given series converges if 1/x > 1 i.e., x < 1 and diverges if 1/x < 1 i.e., x > 1. The test fails for x = 1.
For x = 1, un = 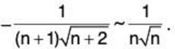
Let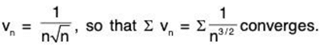
Now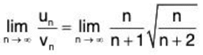
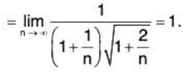
So ∑un and ∑vn converge or diverge together. Since ∑vn converges, therefore ∑un also converges (for x = 1).
Hence the given series converges for x ≤ 1 and diverges for x > 1.
Example 4: Test for the convergence of the series:
(i) 
(ii) 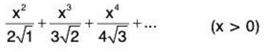
(iii) 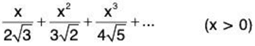
Solution:
(i) 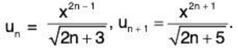
∴ 
By Ratio Test, ∑un converges if 1/x2 > 1 i.e., x2 < 1 i.e., x < 1 and diverges if x2 > 1 i.e., x > 1. The test fails if x = 1.
For x = 1,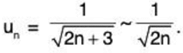
Let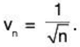
Then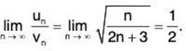
Since ∑vn = ∑1/√n diverges, so ∑un diverges (for x = 1).
Hence the given series converges if x < 1 and diverges if x ≥ 1.
(ii) We have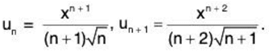
∴ 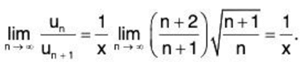
By Ratio Test, ∑un converges if 1/x > 1 i.e., x < 1 and diverges if x > 1. The test fails if x = 1.
For x = 1,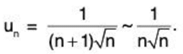
Let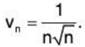
∴ 
Since ∑vn = ∑1/n√n converges, so ∑un converges (for x = 1).
Hence the given series converges if x ≤ 1 and diverges if x > 1.
(iii) We have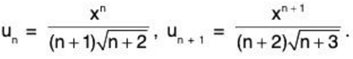
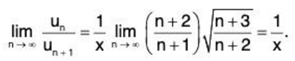
By Ratio Test, ∑un converges if 1/x > 1 i.e., x < 1 and diverges if x > 1. The test fails if x = 1.
For x = 1,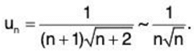
Let
As done in part (ii), ∑un converges if x = 1.
Hence the given series converges if x ≤ 1 and diverges if x > 1.
Example 5: Test for convergence the series:
(i) 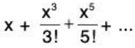 for all Positive values of x.
for all Positive values of x.
(ii) 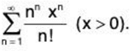
Solution:
(i) 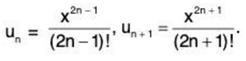
Now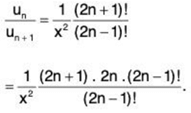
∴ 
Hence, by Ratio Test, ∑un converges.
(ii) We have 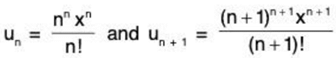
∴ 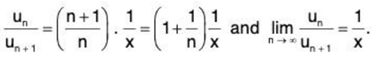
By Ratio test, ∑un converges if 1/x > i.e., x < 1 and diverges if 1/x < 1 i.e., x > 1. For x = 1, we have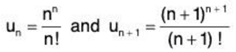
∴ 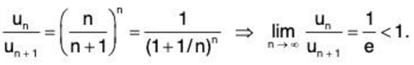
So the given series diverges for x = 1. Hence the given series converges if x < 1 and diverges if x ≥ 1.
Example 6: Test for convergence the series: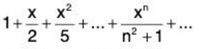
for all positive values of x.
Solution: Ignoring the first term of the series, we have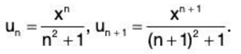
∴ 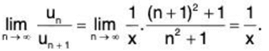
By Ratio Test, ∑un converges if 1/x > 1 i.e., x < 1 and ∑un diverges if x > 1. Ratio Test fails if x = 1.
For x = 1,
Clearly,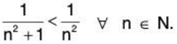
Since ∑1/n2 converges, so by First Comparison Test, 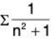 converges.
converges.
Hence ∑un converges for x ≤ 1 and diverges for x > 1.
Example 7: Test for convergence the series with nth term:
(i) 
(ii) 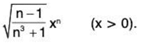
Solution:
(i) 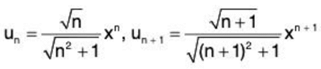
∴ 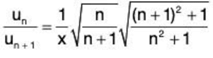
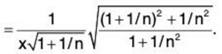
∴ 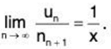 By Ratio Test, the given series converges if 1/x > 1 i.e., x < 1 and diverges if x > 1. The test fails if x = 1.
By Ratio Test, the given series converges if 1/x > 1 i.e., x < 1 and diverges if x > 1. The test fails if x = 1.
For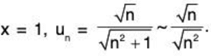
Let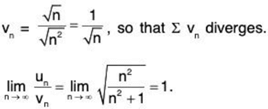
So ∑un and ∑vn converge or diverge together.
Since ∑vn diverges, so ∑un diverges (for x = 1).
Hence the given series converges if x < 1 and diverges if x ≥ 1.
(ii) 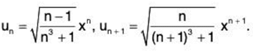
∴ 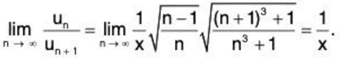
By Ratio Test, the given series converges if 1/x > i.e., x < 1 and diverges if 1/x < 1 i.e., x > 1. The test fails if x = 1.
For x = 1,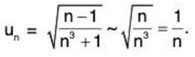
Let
∴ 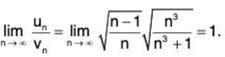
So ∑un and ∑vn converge or diverge together.
Since ∑vn = ∑1/n diverges, so ∑un diverges (for x = 1).
Hence the given series converges if x < 1 and diverges if x ≥ 1.
Example 8: Test for the convergence of the series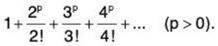
Solution: We have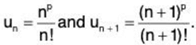
∴ 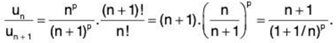
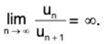 Hence ∑un is convergent, by Ratio Test.
Hence ∑un is convergent, by Ratio Test.
Example 9: Test for the convergence of the series:
Solution: Ignoring the first term, we have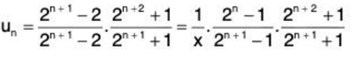
∴ 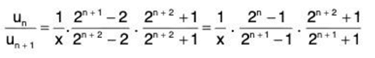
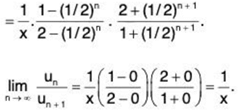
By Ratio Test, ∑un converges if 1/x > 1 i.e., x < 1 and diverges if x > 1. Ratio Test fails if x = 1.
For x = 1,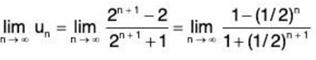
i.e.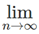 un = 1 ≠ 0. So ∑un diverges for x = 1.
un = 1 ≠ 0. So ∑un diverges for x = 1.
Hence ∑un converges if x < 1 and diverges if x ≥ 1.
Raabe’s Test
Let ∑un be a positive term series such that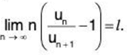
Then (i) ∑un converges if / > 1, (ii) ∑un diverges if / < 1.
The test fails if / = 1.
Note: Raabe's test is applied when D'Alembert's ratio test fails
Proof. Case I. Let / > 1.
We can choose some ε > 0 such that / — ε > 1 or α > 1, α = / - ε.
From (1), there exists a positive integer m such that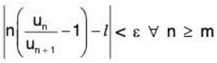
or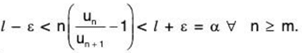
Consider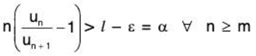
or nun - nun+1 > α un+1 ∀ n ≥ m
or nun - (n + 1)un + 1 > (α - 1) un + 1 ∀ n ≥ m.
Putting n = m, m + 1, m + 2, .... n - 1 and adding, we get
mum - nun > (α - 1) (um+1 + um+2 + ... + un)
or (α - 1) (Sn - Sm) <mum - num < mum, (where Sn = u1 + u2 + ... + um + um+1 + ... + un)
Thus
Sn < Sm + m/α-1 um ∀ n.
where Sm + m/α - 1 um is a fixed positive number.
It follows that the sequence <Sn> is bounded above and so the given series is convergent.
Case II. Let / < 1.
We can choose another ε > 0 such that / + ε < 1.
From (1), there exists a positive integer m1 such that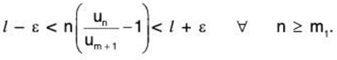
Since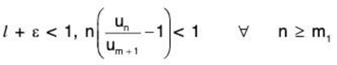
or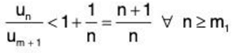
or
Since ∑vn = ∑1/n diverges, so by Second Comparison Test, ∑un diverges.
Case III. Consider the two series 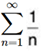 and
and 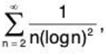 where the first series is divergent and the second series is convergent but for both the series
where the first series is divergent and the second series is convergent but for both the series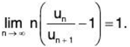
Remark: Raabe’s Test is applied when D’Alembert’s ratio fails.
When Ratio test fails i.e., when 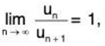 Raabe’s test may be applied.
Raabe’s test may be applied.
Example 1: Test for convergence the series:
(i) 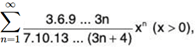
(ii) 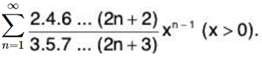
Solution:
(i) 
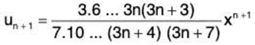
∴ 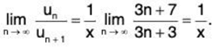
By Ratio Test, ∑un converges if 1/x > 1 i.e., x < 1 and diverges if x > 1. The test fails if x = 1. We shall now apply Raabe’s Test.
For
∴ 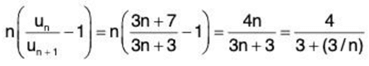
⇒ 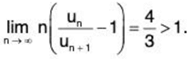
By Raabe’s Test, ∑un converges (for x = 1).
Hence the given series converges for x ≤ 1 and diverges for x > 1.
(ii) 
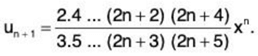
∴ 
By Ratio Test, ∑un converges if 1/x > 1 i.e., x < 1 and diverges if x > 1. The test fails if x = 1.
For x = 1,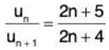
now,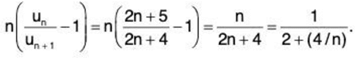
∴ 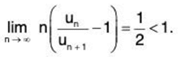
By Raabe’s Test, ∑un diverges (for x = 1)
Hence the given series converges for x < 1 and diverges for x ≥ 1.
Example 2: Examine the convergence of the following series:
(i) 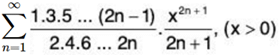
(ii) 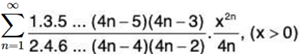
Solution: (i) We have

∴ 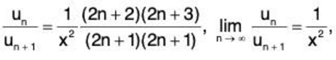
By Ratio test, ∑un converges if 1/x2 > 1 i.e., x < 1 (as x > 0) and diverges if x > 1. The test fails for x = 1.
For x = 1,
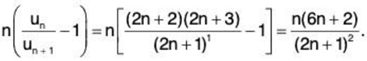
∴ 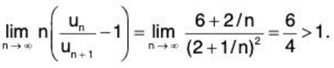
By Raabe’s test, ∑un converges (for x = 1).
Hence the given series converges for x ≤ 1 and diverges for x > 1.
(ii) 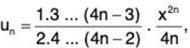

∴ 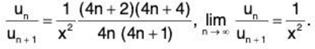
By Ratio test, ∑un converges if 1/x2 > 1 i.e., x < 1 (as x > 0) and diverges if x > 1. The test fails for x = 1.
For x = 1,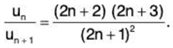
Now
∴ 
By Raabe’s Test, ∑un converges (for x = 1).
Hence the given series converges for x ≤ 1 and diverges for x > 1.
(ii) 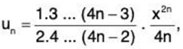

∴ 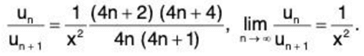
By Ratio test, ∑un converges if 1/x2 > 1 i.e., x < 1 (as x > 0) and diverges if x = 1.
For x = 1,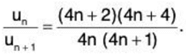
Now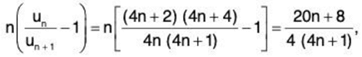
and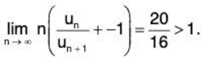
By Raabe’s Test, ∑un converges (for x = 1).
Hence the given series converges for x ≤ 1 and diverges for x > 1.
Example 3: Test for convergence the series: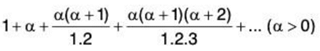
Solution: On ignoring the first term, we have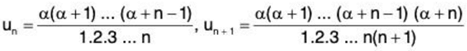
∴ 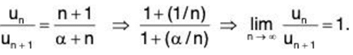
Thus Ratio test fails. We shall now apply Raabe’s test.
∴ 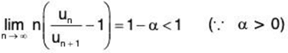
Hence, the given series is divergent.
De Morgan and Bertrand’s Test
If ∑un be a series of positive terms; such that: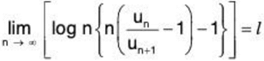
(i) if / > 1, ∑un is convergent
(ii) (ii) if / > 1, ∑un is divergent
Proof: In which follows, we shall compare ∑un with the auxiliary series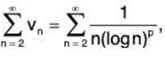
which is known to be convergent if p > 1 and divergent if p ≤ 1.
Now, we have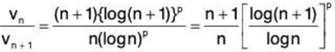
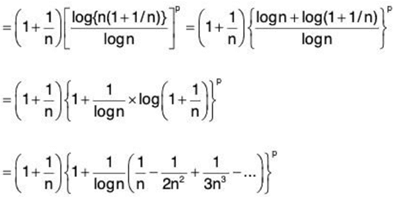
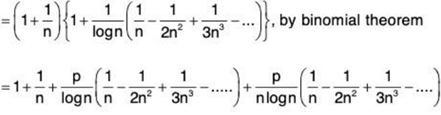
Thus ...(1)
...(1)
Case (i). Let / > 1. Choose a number p such that / ≥ p > 1.
By comparison test of the second type the series ∑un will be convergent if there exists a positive integer m such that [ n ≥ m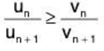
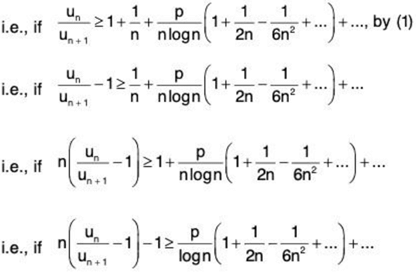
 n ≥ p + terms containing n or log n in the denominator ...(2)
n ≥ p + terms containing n or log n in the denominator ...(2)
Taking limits on both sides of (2) as n → ∞ we get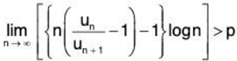
⇒ / > p ⇒ I > 1 a s p > 1.
Thus, ∑un converges if / > 1.
Case (ii). Proceed as in case (i) yourself.
Logarithmic Ratio Test
If ∑un be a series of positive terms; such that:
(i) if / > 1, ∑un is convergent
(ii) if / > 1, ∑un is divergent
(iii) if / > 1, ∑un may converge or diverge. So test fails.
Proof: Let / > 1 and let us choose ε > 0 such that / - ε > 1. Let / - ε = λ so that / > 1.
Now
⇒ there exists a positive integer m such that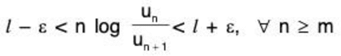
⇒ 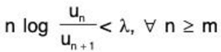
⇒ un/un+1 > eλ/n, [ n ≥ m ...(1)
We now that the sequence <(1 + 1/n)n> converges to e and hence
e ≥ (1 + 1/n)n, [ n ∈ N
⇒ eλ/n ≥ (1 + 1/n)λ ... (2)
From (1) and (2), we have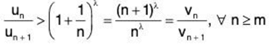 ...(3)
...(3)
where vn = 1/nλ.
Since λ > 1, so ∑vn converges. Then, using comparison test of second type it follows that the given series ∑un also converges.
(ii) Prove as in part (i).
Note 1. The above Logarithmic test is alternative to Raabe’s test and should be used when D'Alembert’s ratio test fails and when either e occurs in un/un+1 or n occurs as an exponent in un/un+1.
Note 2. When Raabe's test fails we may use De Morgan’s and Bertrand’s test given below. Again, when logarithmic test fails we may use second logarithmic ratio test.
Second Logarithmic Ratio Tests
Let ∑un be a series of positive terms such that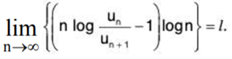
Then the series is
(i) convergent if / > 1
(ii) divergent if / < 1
(iii) no other decision is possible if / = 1.
Proof: In what follows, we shall compare ∑un with the auxiliary series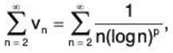
which is known (refer Art.) to be convergent if p > 1 and divergent if p ≤ 1. Now, we have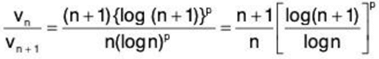
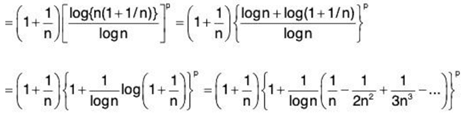
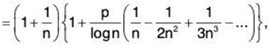
by binomial theorem
Thus .... (1)
.... (1)
Case (i). Let / > 1. Choose a number p such that / ≥ p > 1.
By comparison test of the second type, the series ∑un will be convergent if there exists a positive integer m such that [ n > m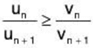
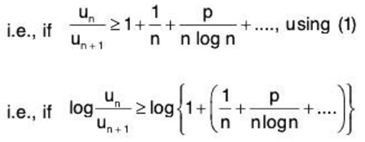
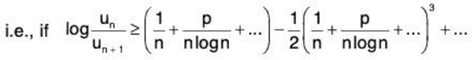
[ ∵ log (1 + x) = x - x2/2 + x3/3 + .... ]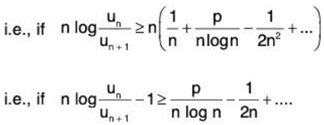
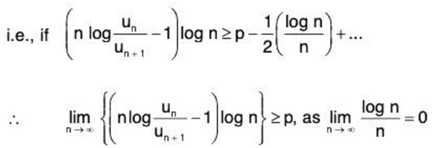
or / ≥ p. But p > 1, so / > 1.
Hence the given series ∑un converges if / > 1.
(ii) Proceed as in case (i) yourself.
Example 1: Examine the convergence of the following series:
(i) 
(ii) 
(iii) 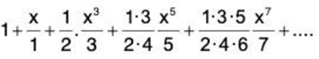
(iv) 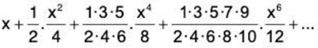
Solution: (i) Here, we have
Here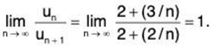
Hence ratio test fails and we now apply Raabe’s test.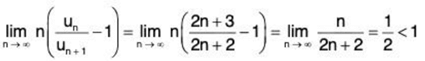
(ii) 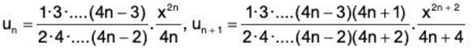
∴ 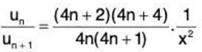 ....(1)
....(1)
and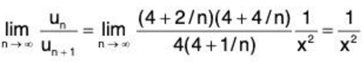
Hence by ratio test, ∑un converges if 1/x2 > 1, i.e., x2 < 1, i.e., x < 1 (as x > 0) and diverges if 1/x2 < 1, i.e., x2 > 1, i.e., x > 1. The test fails if x = 1. In that case, from (1), we have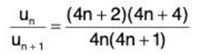
∴ 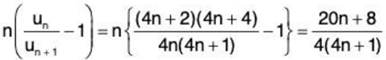
and hence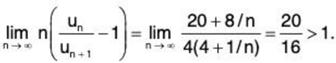
Hence, by Raabe’s test, ∑un is convergent.
Thus the given series converges if x ≤ 1 and diverges if x > 1.
(iii) Omitting the first term of the given series as it will not change the nature of the series, we obtain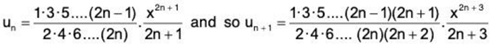
∴ 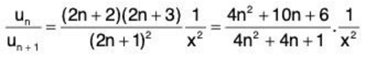 ...(1)
...(1)
Now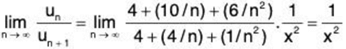
∴ By ratio test ∑un converges if 1/x2 > 1, i.e., if x2 < 1 and diverges if 1/x2 < 1, i.e., if x2 > 1. When 1/x2 = 1, i.e., x2 = 1, the ratio test fails. We shall now apply Raabe’s test.
From (1), for x2 = 1,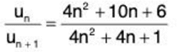
∴ 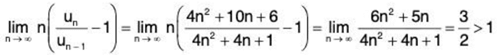
Hence, by Raabe’s test, ∑un converges for x2 = 1.
Thus the given series converges if x2 ≤ 1 and diverges if x2 > 1.
(iv) Omitting the first term, the nth term of the resulting series is
[Here the nth term of the A.P., 1, 5, 9, ... is 1 + (n - 1) × 4, i.e., 4n - 3 and the nth term of the A.P., 2, 6, 10, ... is 2 + (n - 1) × 4, i.e., 4n - 2]
and so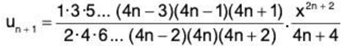
∴ 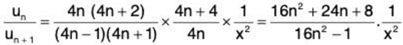 ...(1)
...(1)
So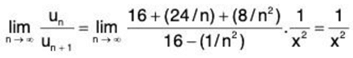
∴ By ratio test ∑un converges if 1/x2 > 1, i.e., if x2 < 1 and diverges if 1/x2 < 1, i.e., if x2 > 1. When 1/x2 = 1, i.e., x2 = 1, the ratio test fails. We shall now apply Raabe’s test.
From (1), for x2 = 1,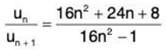
∴ 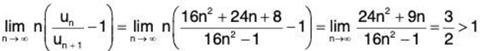
Hence, by Raabe's test, ∑un converges.
Thus the given series converges if x2 ≤ 1 and diverges if x2 > 1.
Example 2: Test the convergence of the following series
(i) 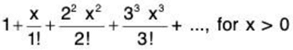
(ii) 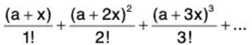
Solution: (i) Omitting the first term, we have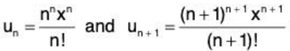
Now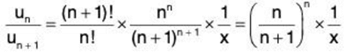 ....(1)
....(1)
∴ 
By ratio test, ∑un converges if 1/ex > 1, i.e., if x < 1/e and diverges if 1/ex < 1, i.e., if x > 1/e. When 1/ex = 1, i.e., x = 1/e, the test fails. Since un/un+1 will involve e for x = 1/ e, we shall apply logarithmic test.
For x = 1/e, from (1)
∴ 
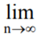 n {log e - n log (1 + 1/n)}
n {log e - n log (1 + 1/n)}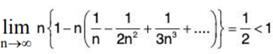
Hence, by logarithmic test, ∑un diverges.
Thus the given series converges if x < 1/e and diverges if x ≥ 1/e.
(ii) Here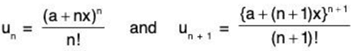
Now,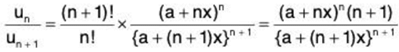
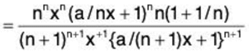
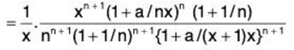
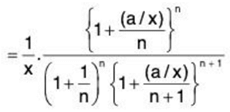 ...(1)
...(1)
Hence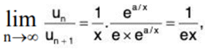
as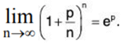
By ratio test, ∑un converges if 1/ex > 1, i.e. if x < 1/e and diverges if 1/ex < 1, if x > 1/e When 1/ex = 1, i.e., x = 1/e, the test fails. We now apply logarithmic test.
For x = 1/e, from (1),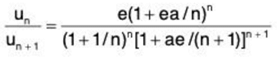
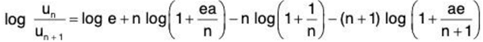

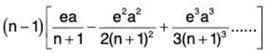
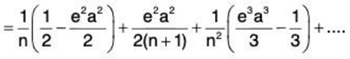
⇒ 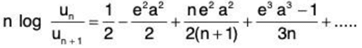
⇒ 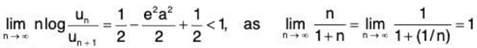
Hence, by logarithmic test, ∑un diverges.
Thus the given series converges if x < 1/e and diverges if x ≥ 1/e.
Example 3: Test for converges the following series:
(i) 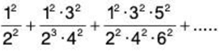
(ii) 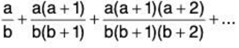
Solution: (i) Here, we have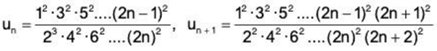
∴ 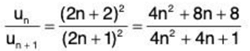 ...(1)
...(1)
Here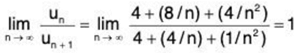
Hence the ratio test fails and we now apply Raabe’s test.
Using (1),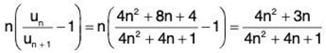 ...(2)
...(2)
∴ 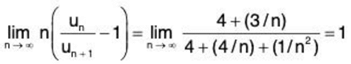
Hence the Raabe’s test fails and we now apply De-Morgan’s and Bertrand’s test. From (2),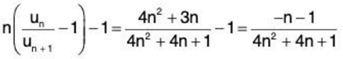
∴ 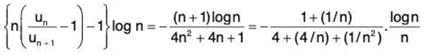
and so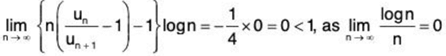
Hence, by De-Morgan’s and Bertrand’s test, ∑un diverges.
(ii) Here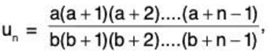
and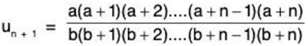
∴ 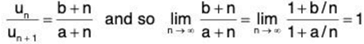 ...(1)
...(1)
Hence the ratio test fails and we now apply Raabe’s test. Using (1),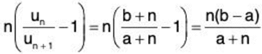 ...(2)
...(2)
∴ 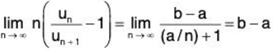
Hence, by Raabe’s test, ∑un converges if b - a > 1 and diverges if b - a < 1. When b - a = 1. Raabe’s test fails and we now apply De-Morgan's and Bertrand’s test.
For b - a = 1, from (2), 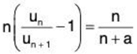
∴ 
∴ 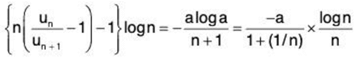
So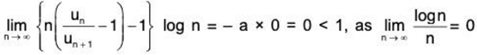
Hence, by De-Morgan’s and Bertrand's test, ∑un diverges. Thus the given series converges if b - a > 1 and diverges if b - a ≤ 1.
Example 4: Test for convergence the following series
(i) 
(ii) x + x1 + 1/2 + x1 + 1/2 + 1/3 + x1 + 1/2 + 1/3 + 1/4 + ...
Solution: (i) Omitting the first term, we have
∴ 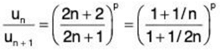 ...(1)
...(1)
Here 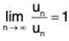 and so ratio test fails.
and so ratio test fails.
We shall now apply logarithmic test, Using (1), we get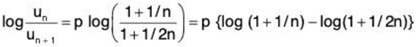

= p(1/2n - 3/8n2 + 7/24n3 + ....)
∴  ...(2)
...(2)
So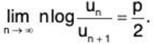
Hence ∑un converges if p/2 > 1, i.e., if p > 2 and diverges if p/2 < 1, i.e., if p < 2 and the test fails if p = 2.
For p = 2, from (2).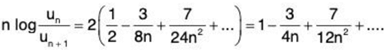
∴ 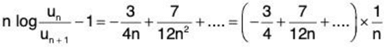
∴ 
Hence by second logarithmic ratio test ∑un diverges for p = 2.
Thus the given series converges if p > 1 and diverges if p ≤ 2.
(ii) Here, un = x1 + 1/2 + ... + 1/n, un+1 = x1 + 1/2 + ... + 1/n + 1/(n +1)
∴  ...(1)
...(1)
Here ratio test fails and we now apply logarithmic test.
From (1),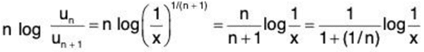 ...(2)
...(2)
∴ 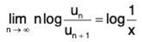
Hence ∑un converges if log (1/x) > 1, i.e., if 1/x > e, i.e., if x < 1/e and ∑un diverges if log (1/x) < 1, i.e., if x > 1/e. When x = 1/e, the test fails and we shall now apply second logarithmic test
For x = 1/e, from (2)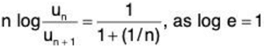

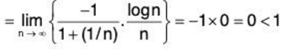
Hence ∑un is divergent for x = 1/e.
Thus, the given series converges if x < 1/e and diverges if x ≥ 1/e
Gauss Test
Theorem: Let 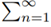 an be a series with positive terms. Assuming that there exists a real number p, a real number r > 1 and a real bounded sequence {Bn}∞n=1 such that for all n
an be a series with positive terms. Assuming that there exists a real number p, a real number r > 1 and a real bounded sequence {Bn}∞n=1 such that for all n
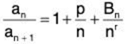
Then the series 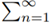 converges if and only if p > 1.
converges if and only if p > 1.
Almost immediately we see that this test is somehow an improved version of Raabe’s test. The only difference is the number r, which in the former test was explicitly set to 2. So Gauss’ test is more general, allowing us to decide convergence of more series. Not surprisingly the proof is very similar.
Proof. If we start with p > 1, then for sufficiently large n we have (for negative terms of {Bn})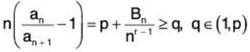
or (for positive terms of {Bn})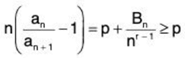
Since in both cases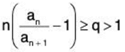
by using Raabe’s test we can conclude that the series  an converges.
an converges.
As for the other part of equivalence, we will assume that the series 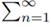 an converges and p = 1. By using Bertrand’s test we get
an converges and p = 1. By using Bertrand’s test we get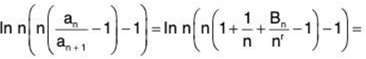
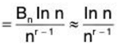
With L’Hopital’s rule we get 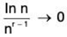 (as n tends to infinity) and therefore the series
(as n tends to infinity) and therefore the series 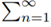 an diverges. A contradiction.
an diverges. A contradiction.
If the series 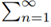 an converges and p < 1 then (for sufficiently large n)
an converges and p < 1 then (for sufficiently large n)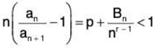
and according to Raabe’s test the series 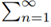 an diverges.
an diverges.
A contradiction. Thus p > 1.
Theorem: Let 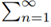 an be a series with positive terms. Assuming that there exist a real number p, a real number p, a real number r > 1 and a real bounded sequence {Bn} such that for all n.
an be a series with positive terms. Assuming that there exist a real number p, a real number p, a real number r > 1 and a real bounded sequence {Bn} such that for all n.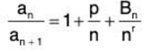 ... (1)
... (1)
The series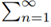 an diverges if and only if p ≤ 1.
an diverges if and only if p ≤ 1.
Proof: Let 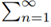 an diverges if and only if p ≤ 1. Then for sufficiently large n.
an diverges if and only if p ≤ 1. Then for sufficiently large n.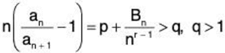
and by Raabe’s test the series 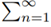 an converges. A contradiction (hence p ≤ 1).
an converges. A contradiction (hence p ≤ 1).
If p = 1 then by using Bertrand’s test (theorem)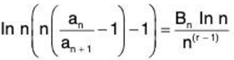
With L’Hospital’s rule we get 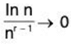 (as n tends to infinity) and therefore the series
(as n tends to infinity) and therefore the series  an diverges.
an diverges.
If p < 1 then for sufficiently large n
We finish the proof with Raabe’s test.
An example. We want to determine the character of the series 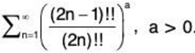
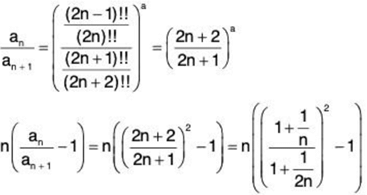
With (x → ∞)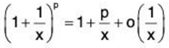
we get the final result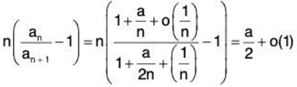
According to Raabe’s test, the series converges when a > 2 and diverges when a < 2 but we get no information when a = 2. We try Gauss’ test:
First, we try to find p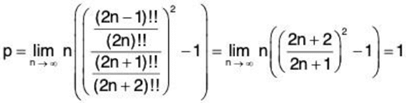
Second, we find An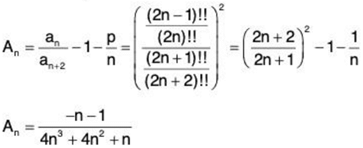
Third, we try to find r > 1 such that Bn = Annr is bounded
If we set r = 2 then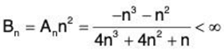
And because p = 1 the series 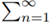
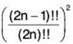 diverges.
diverges.
Therefore, according to Gauss and Raabe’s test, the series 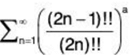 converges when a > 2 and diverges when a ≤ 2.
converges when a > 2 and diverges when a ≤ 2.
Kummer’s test
Here comes probably the most powerful test for convergence, since it applies to all series with positive terms.
Theorem: Let 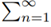 an be a series with positive terms. Then the series converges if and only if there exist a positive number A, positive numbers pn and a number N ∈ N such that for all n > N
an be a series with positive terms. Then the series converges if and only if there exist a positive number A, positive numbers pn and a number N ∈ N such that for all n > N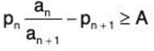
The series diverges if and only if there exist positive numbers pn such that 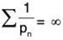 and a number N ∈ N such that for all n > N
and a number N ∈ N such that for all n > N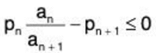 ...(2)
...(2)
Proof: First we prove the convergence. For the right-to-left implication, we adjust the equation (1)
pnan - pn+1an+1 ≥ Aan+1
With qn = pn/A we can write
qnan - qn+1an+1 ≥ an+1
Since we know the left side of upper inequality, we can construct a sequence {Bn}∞n=1 such that
qnan - qn+1an+1 = Bn+1an+1, ∀n Bn ≥ 1
The sequence {qnan}∞n=1 is positive and decreasing (follows from (3)).
Therefore it has a limit
0 ≤ 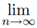 anqn < q1a1
anqn < q1a1
Thus the series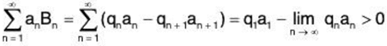
converges. And because Bn ≥ 1 for all n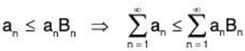
In words, the series 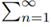 anBn converges and creates an upper bound for the series
anBn converges and creates an upper bound for the series  an, therefore the series
an, therefore the series an must converge as well. This is nothing more then just a first comparison criteria. We showed that finding numbers pn is equally hard as finding a convergent series ∑bn which creates an upper bound for the series ∑an in the first comparison test. For left-to-right implication, let p1a1 be a positive number. Now we assume the existence of positive monotonous sequence {Bn}∞n=1
an must converge as well. This is nothing more then just a first comparison criteria. We showed that finding numbers pn is equally hard as finding a convergent series ∑bn which creates an upper bound for the series ∑an in the first comparison test. For left-to-right implication, let p1a1 be a positive number. Now we assume the existence of positive monotonous sequence {Bn}∞n=1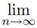 Bn = ∞ ...(4)
Bn = ∞ ...(4)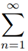 anBn =P1a1 + a1B1
anBn =P1a1 + a1B1
Now we shift the index n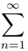 an+1 Bn+1 = P1a1
an+1 Bn+1 = P1a1
We define the sequence {pnan}∞n=1 this way
pn+1an+1 =pnan - an+1 Bn+1
where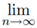 pnan = p1a1 -
pnan = p1a1 - 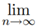
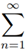 ak+1Bk+1 = 0
ak+1Bk+1 = 0
So, using (4) we have (for sufficiently large n)
pnan - pn+1an+1 = an+1Bn+1 ≥ Aan+1 where A > 0
And finally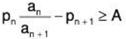
hence the number pn are found.
Remark : In fact, the requirement (4) is not necessary as any positive and monotonous sequence {Bn} with 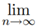 Bn = A ≥ 1 is totally sufficient (where A is an arbitrary constant).
Bn = A ≥ 1 is totally sufficient (where A is an arbitrary constant).
For example, let ∑an be a convergent series. If we let Bn = 1 for all n and we construct numbers pn using the terms from ∑an 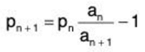
Kummer’s test will confirm the convergence of series ∑an (as would first comparison test). Now the divergence part.
Proof: For the right-to-left implication, we have ∑1/pn = ∞ and from (2) we get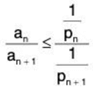
We can conclude the divergence of series  an by using the second comparison test. To prove left-to-right implication (when
an by using the second comparison test. To prove left-to-right implication (when  an is divergent), we can assume, according to the theorem, the existence of positive and monotonous sequence Bn such that
an is divergent), we can assume, according to the theorem, the existence of positive and monotonous sequence Bn such that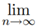 Bn = 0 ...(5)
Bn = 0 ...(5)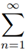 anBn = ∞
anBn = ∞
We have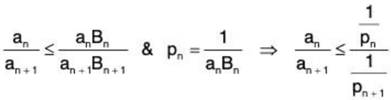
we get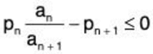
It is not difficult to see, that ∑1/pn = ∞ and pn > 0 for all n, thus we found the numbers we were looking for.
Remark: Again, the requirement (5) is not necessary as any positive and non-increasing {Bn} 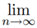 Bn = A > 0 will do the trick (as it is the monotony we are interested in).
Bn = A > 0 will do the trick (as it is the monotony we are interested in).
As in the previous remark, if ∑an is a divergent series and if we let Bn = 1 for all n then Kummer’s test will confirm the divergence.
Remark: To sum it up, Kummer’s test is very powerful because it really works for all the series with positive terms. On the other hand, using this test is equally difficult as using the first and second comparison test. The true strength of this test therefore lies in the numbers pn. That is, the form of this test is a masterpiece, not its contents.
To demonstrate the power of Kummer’s test, we show that Raabe’s test and Bertrand’s test are in fact its corollaries. As for Raabe’s test, if we set pn = n, we get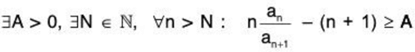
 compare with for convergence and
compare with for convergence and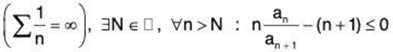
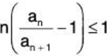 compare with for divergence.
compare with for divergence.
We see, that what we can decide with Raabe’s test, we can also decide with Kummer’s test (with pn = n) and vice versa, thus they are equivalent.
As for Kummer’s version of Bertrand’s test, we set pn = n In n and put it into the left side of (1):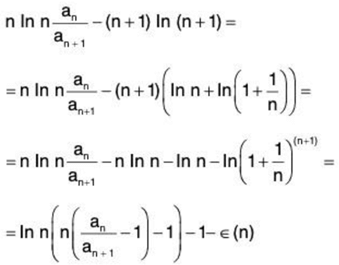
so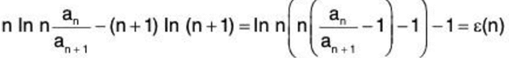 .. (6)
.. (6)
Where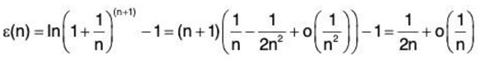
We go back to (1). With (6), if
∃A > 0, ∃N ∈ N, ∀n > N : ...(7)
...(7)
then the series  an is convergent.
an is convergent.
Compare with Bertrand’s test:
If ∃A > 0, ∃N ∈ N, ∀n > N: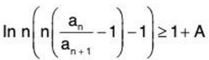 ...(8)
...(8)
then the series 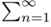 an is convergent.
an is convergent.
Since ε(n) can get arbitrarily small as n tends to infinity, we can hide it inside the positive constant A. Thus (7) and (8) are equivalent.
Divergence is a bit different and we will see that in this case, the tests are not equivalent. That is, Kummer’s test is slightly stronger. It is because now we have zero as a sharp border, while the constant A from the previous case was quite flexible.
With (2), (6) and pn = n In n : if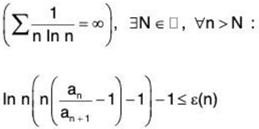
then the series 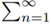 is divergent. Compare with Bertrand’s test (see (5)) : If
is divergent. Compare with Bertrand’s test (see (5)) : If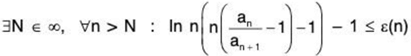
then the series 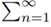 an is divergent.
an is divergent.
Now let's consider the series 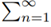 an, where an = 1/nInn. Using Bertrand’s test
an, where an = 1/nInn. Using Bertrand’s test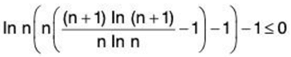
(n + 1) In (n + 1) - n In n - In n - 1 = (n + 1) In (1 + 1/n) - 1 = ε(n) ≤ 0 → false Using Kummer’s test (with pn = n In n)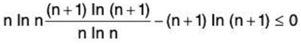
0 ≤ 0 → true
There is infinite number of series that can be decided only with Kummer’s version of Bertrand’s test, but if we use limit, the tests are equivalent.
Root Test
Test IX. Cauchy’s nth Root Test
Let ∑un be a positive terms series such that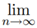 (un)1/n = I. ...(1)
(un)1/n = I. ...(1)
Then (i) ∑un converges if / < 1, (ii) ∑un diverges if / > 1. Test fails if / = 1.
Proof : Case I. Let / < 1.
We can choose some ε > 0 such that / + ε < 1 or α < 1, α = / + ε.
Using (1), there exists a positive integer m1 such that
I (un)1/n - I | < ε ∀ n ≥ m1.
or / - ε < (un)1/n < / + ε ∀ n ≥ m1.
Consider (un)1/n < / + ε = α ∀ n ≥ m1.
un < αn ∀ n ≥ m1. ...(2)
Since ∑αn = α + α2 + .. being a geometric series with common ratio α < 1 is convergent, so by First Comparison Test as applied in (2), ∑un is convergent.
Case II. Let / > 1.
We can choose another ε > 0 such that / — ε > 1 or β > 1, β = / - ε.
Using (1), there exists a positive integer m2 such that
I (un)1/n - / I < ε ∀ n ≥ m2.
or / - ε < (un)1/n < / + ε ∀ n ≥ m2.
Consider l - ε < (un)1/n ∀ n ≥ m2.
or βn < un ∀ n ≥ m2. ...(3)
Since ∑βn being a geometric series with common ratio β > 1 is divergent, so by First Comparison Test as applied in (3), ∑un is divergent.
Case III. We shall give examples of two series : one convergent and the other divergent, but both satisfying 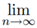 (un)1/n = 1.
(un)1/n = 1.
The series ∑un = ∑1/n is divergent, but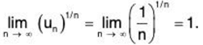
The series ∑un = ∑1/n2 is convergent, but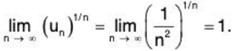
|
98 videos|34 docs|32 tests
|
FAQs on Series of Real Numbers- I - Mathematics for Competitive Exams
| 1. What is a series of real numbers? |  |
| 2. How do you test the convergence of a series of real numbers? |  |
| 3. What is the comparison test for convergence of a series? |  |
| 4. How does the ratio test work in testing the convergence of a series? |  |
| 5. What is the alternating series test and when is it applicable? |  |





















