Year 10 Exam > Year 10 Notes > Mathematics for GCSE/IGCSE > Set Notation & Venn Diagrams
Set Notation & Venn Diagrams | Mathematics for GCSE/IGCSE - Year 10 PDF Download
Set Notation
What is a set?
- A set is a group of elements. These elements can vary and might include numbers, letters, coordinates, and more.
- You can represent a set by listing its elements within braces {}. For example, {1, 2, 3, 6} represents a set containing the factors of 6.
- When elements in a set follow a specific rule, you can express this using a colon within the braces {... : ...}. The section before the colon signifies the type of element, while the part after the colon denotes the rule.
- Sets commonly consist of numbers, but they can also include coordinates. For instance, {(x, y): y = 2x - 1} describes a set of points lying on the line y = 2x - 1.
What do I need to know about set notation?
- ℰ is the universal set (the set of everything)
- e.g. if talking about factors of 24 then ℰ = {1, 2, 3, 4, 6, 8, 12, 24}
- You may see alternative notations used for calligraphic E
- U is a common alternative
- S or the Greek letter ξ (xi) may also be seen
- ∅ is the empty set (the set of with no elements}
- e.g. {x : x is an even prime bigger than 5} = ∅ as there are no even primes bigger than 5
- We normally use upper case letters to represent sets (A, B, C, ...) and lower case letters to represent elements (a, b, c, ...)
- n(A) is the number of elements in set A
- e.g. n({1, 4, 9}) = 3
- Note n(∅) = 0 as there are no elements in the set but n({0}) = 1 as there is 1 element in the set
- a ∈ A means a is an element of A (a is in the set A)
- e.g. If x ∈ {1, 4, 9} then x is either 1, 4 or 9
- A ⊆ B means A is a subset of B
- This means every element in A is also in B
- e.g. {students in class Y that pass the exam} ⊆ {students in class Y}
- Putting a cross through the symbol means it is not true
- Similar to ≠ meaning not equal
- a ∉ A means a is not an element of the set A
- A ⊈ B means A is not a subset of B
- A ⊄ B means A is not a proper subset of B
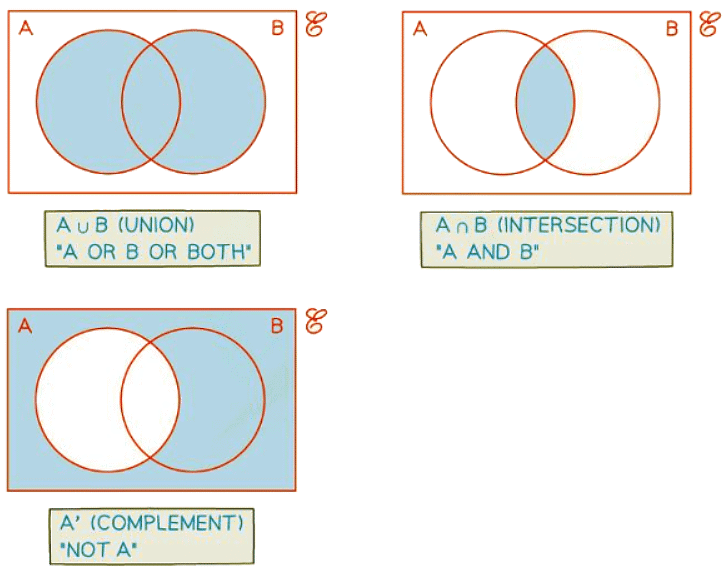
- A ∩ B means the intersection of A and B (the overlap of A and B)
- This is the set of elements that are in both set A and set B
- A ∪ B means the union of A and B (everything in A or B or both)
- This is the set of elements that are in at least one of sets
- A' is the complement of A
- This is thought of as “not A” (everything outside A)
- This is the set of elements that are not in A
Sets & Venn Diagrams
What is a Venn diagram?
- A Venn diagram is a visual tool used to show relationships between sets and their elements.
- It consists of a rectangle that represents the universal set (ℰ) and circles that represent individual sets.
- Circles in a Venn diagram can overlap to show common elements between sets.
What do the different regions mean on a Venn diagram?
- A' is represented by the regions that are not in the A circle
- A ∩ B is represented by the region where the A and B circles overlap
- A ∪ B is represented by the regions that are in A or B or both
Question for Set Notation & Venn DiagramsTry yourself: What is the universal set?View Solution
The document Set Notation & Venn Diagrams | Mathematics for GCSE/IGCSE - Year 10 is a part of the Year 10 Course Mathematics for GCSE/IGCSE.
All you need of Year 10 at this link: Year 10
|
75 videos|394 docs|60 tests
|
FAQs on Set Notation & Venn Diagrams - Mathematics for GCSE/IGCSE - Year 10
| 1. What is a set in mathematics? |  |
Ans. A set in mathematics is a collection of distinct objects, considered as an object in its own right. These objects can be anything from numbers to shapes to even other sets.
| 2. How are sets usually represented in mathematics? |  |
Ans. Sets are typically represented using curly braces { } to enclose the elements of the set. For example, the set of even numbers less than 10 can be written as {2, 4, 6, 8}.
| 3. What is a Venn diagram and how is it used in set theory? |  |
Ans. A Venn diagram is a visual representation of sets using overlapping circles. It helps to illustrate the relationships between different sets and their elements, making it easier to understand concepts such as intersections and unions.
| 4. How do you find the intersection of two sets? |  |
Ans. The intersection of two sets is the set of elements that are common to both sets. To find the intersection, you list all the elements that appear in both sets. For example, the intersection of the sets A = {1, 2, 3} and B = {2, 3, 4} is {2, 3}.
| 5. Can sets contain duplicates or repeat elements? |  |
Ans. No, sets in mathematics do not contain duplicates or repeat elements. Each element in a set is unique, and if an element is repeated, it is only counted once in the set.
Related Searches
















