This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Set Theory (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Set Theory - 2
Try yourself:In a school, 100 students were offered Hindi as an optional subject and 70 students were offered French and Sanskrit each. Out of these, 63 were offered Hindi only, 47 were offered French only, 12 were offered Hindi and French only and 6 were offered French and Sanskrit only. The total number of students in the school is
Explanation

Total number of students = n(H ∪ S ∪ F)
= n(H) + n(S) + n(F) - n(H ∪ S) - n(S ∪ F) - n(H ∪ F) + n(H ∩ S ∩ F)
= 100 + 70 + 70 - 17 - 25 - 11 + 5 = 192
Or adding the various numbers in different regions in the Venn diagram, total number of students
= 63 + 12 + 47 + 25 + 6 + 39 = 192
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
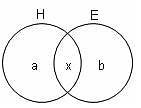
Try yourself:In a group of 1000 people, 750 people can speak Hindi and 400 people can speak English. In the group, all the people speak at least one out of the two languages. How many people can speak only Hindi?
Explanation

The Venn diagram for the situation is as shown above.
In the Venn diagram, H denotes the set of people who speak Hindi and E denotes the set of people who speak English.
So, a + x = 750 ... (i)
x + b = 400 ... (ii)
Adding equations (i) and (ii), we get a + x + b + x = 1150 ... (iii)
But a + x + b = 1000 ... (iv)
Putting this value of a + x + b from equation (iv) into equation (iii), we get
1000 + x = 1150
Or x = 150 ... (v)
Putting this value of x from equation (v) into equation (i) and solving for a, we get
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
Try yourself:The shaded area in the given diagram represents

Explanation
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
Try yourself:Out of 100 students in Holy Christ School of Science, 40 study Physics and 70 study Mathematics. If there are at least 20 students who study neither Mathematics nor Physics, what is the possible range of students who study both Mathematics and Physics?
Explanation
Total students = Physics + Mathematics – Both 'Mathematics' and 'Physics' + Neither 'Mathematics' nor 'Physics'
Here's what we know:
Total = 100
Physics = 40
Mathematics = 70
Both (B) = Unknown
Neither (N) = Unknown
or we have
100 = 40 + 70 - Both + Neither
100 = 110 - B + N (Let's isolate 'B' since we are solving for possible values of 'B')
B = N + 10
Now, the minimum value of N is 20 and the maximum value can be 30.
Thus, the minimum value of B is 30 and the maximum value of B is 40.
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
Try yourself:In a survey of population of 450 people, it is found that 205 people can speak English, 210 people can speak Hindi and 120 people can speak Tamil. If 100 people can speak both English and Hindi, 80 people can speak both English and Tamil, 35 people can speak Hindi and Tamil, and 20 people can speak all the three languages, then find the number of people who cannot speak English, Hindi, or Tamil.
Explanation
n(E ∪ H ∪ T) = n(E) + n(H) + n(T) - n(E ∩ H) - n(E ∩ T) - n(H ∩ T) + n(E ∩ H ∩ T)
= 205 + 210 + 120 - 100 - 80 - 35 + 20
= 340
Number of people who cannot speak English, Hindi, or Tamil = 450 - 340 = 110
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
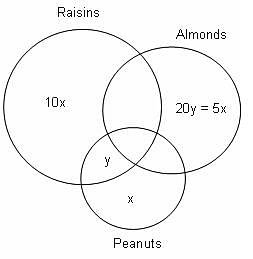
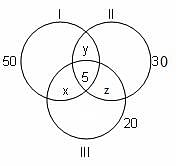
Try yourself:Each of 435 bags contains at least one of the following three items: raisins, almonds, and peanuts; 210 bags contain almonds. The number of bags that contain only raisins is 10 times the number of bags that contain only peanuts. The number of bags that contain only almonds is 20 times the number of bags that contain only raisins and peanuts. The number of bags that contain only peanuts is one-fifth the number of bags that contain only almonds. How many bags contain only one kind of item?
Explanation

There are a total of 435 bags and 210 bags contain almonds.
From the diagram,
20y = 5x
y = x/4
Now, 435 = {Almonds} + 10x + y + x
435 = 210 + 10x + (x/4) + x
x = 20
Hence, number of bags that contain only one kind of item = 10x + x + 5x = 16x
= 320
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
Try yourself:A merchant surveyed 400 people to determine the way they learned about an upcoming sale. The survey showed that 180 learned about the sale from radio, 190 from television, 190 from newspaper, 80 from radio and television, 90 from radio and newspaper, 50 from television and newspaper and 30 from all the three. How many people did not come to know about the sale from any of these sources?
Explanation
We can calculate by using the formula,
n(a) + n(b) + n(c) - n(a ∩ b) - n(b ∩ c) - n(c ∩ a) + n(a ∩ b ∩ c)
n(a ∪ b ∪ c) = 180 + 190 + 190 - 80 - 90 - 50 + 30 = 370
Number of People did not come to know about the sale from any of these sources = (400 - 370) = 30
Thus, 30 people did not come to know about the sale from any of these sources.
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
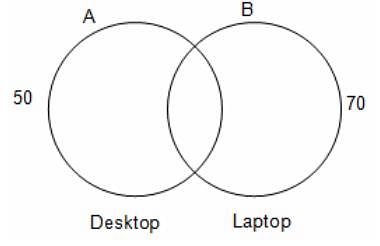
Try yourself:In a survey at Massachusetts Institute of Technology, 80 students were asked whether they used laptop or desktop or both. Of these, 50 students said they used desktop and 70 said they used laptop. What could be the respective minimum and maximum numbers of students who used both desktop and laptop?
Explanation
n (A ∩ B) = n(A) + n(B) - n (A ∪ B)

For min n (A ∩ B), n (A ∪ B) should be maximum, which is 80.
Hence, n(A ∩ B) min = 50 + 70 - 80 = 40
Also, A ∩ B is maximum when all desktop users are also laptop users. Hence, 50.
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
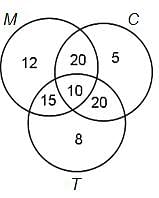
Try yourself:An investigator interviewed 100 students to determine their preferences for the three drinks: milk (M), coffee (C) and tea (T). He reported the following: 10 students liked M, C and T, 20 liked M and C only, 30 liked C and T, 25 liked M and T, 12 liked M only, 5 liked C only and 8 liked T only. How many did not like any of the three drinks?
Explanation

Number of people who liked at least one drink = 12 + 15 + 20 + 10 + 20 + 5 + 8 = 90
Number of people who liked none of the drinks = 100 - 90 = 10
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
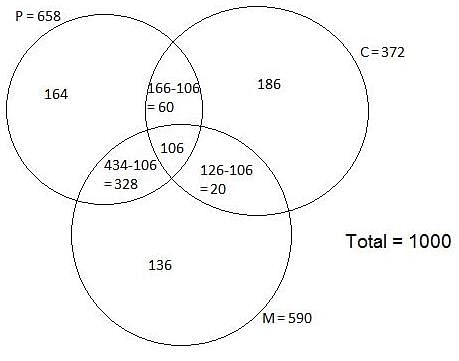
Try yourself:The result of an exam is given below.
Out of 1000 students who appeared-
(i) 658 failed in Physics
(ii) 166 failed in Physics and Chemistry
(iii) 372 failed in Chemistry and 434 failed in Physics and Maths
(iv) 590 failed in Maths and 126 failed in Maths and Chemistry
Find the number of students who failed in Physics but not in Chemistry or Maths.
Explanation

Let number of students who failed in all the subjects be x.
1000 = 658 + 372 + 590 - 166 - 126 - 434 + x
x = 106
Number of students who failed in Physics but not in Chemistry or Maths = 658 - 60 - 106 - 328 = 164
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
Try yourself:A survey was conducted to know the number of households who owned either car or bike or both car and bike. It was determined that out of 200 households that were surveyed, 80 used neither bike nor car, 60 used only bike, and for every household that used both car and bike, 3 used only car. How many of the 200 households surveyed used both car and bike?"
Explanation
Total = 200
Neither having car nor bike = 80
Only bike = 60
Only car = 3 (using both car and bike)
Only bike + Only car + Neither of both + Both car and bike = Total
60 + 3 x {Both car and bike} + 80 + {Both car and bike} = 200
4 x {Both car and bike} = 60
Therefore, having both car and bike = 15
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
Try yourself:Visitors to a modern art museum who watched a certain Picasso painting were asked to fill in a short questionnaire, indicating whether they had enjoyed looking at the picture, and whether they felt they had understood it. According to the results of the survey, all 120 visitors who did not enjoy the painting also did not feel they had understood the painting, and the number of visitors who enjoyed the painting was equal to the number of visitors who felt they had understood the painting. If 3/4th of the visitors who answered the questionnaire both enjoyed the painting and felt they had understood the painting, how many visitors answered the questionnaire?
Explanation
Let the total number of people who filled the questionnaire be x.
If 120 didn't enjoy; then x - 120 enjoyed.
Also (3x/4) = those who enjoyed and understood
Total = x - 120 + x - 120 - (3x/4) + 120 = x
⇒ (5x/4) - 120 = x
⇒ (x/4) = 120
⇒ x = 480
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
Try yourself:In a survey of 100 people about their movie-going habits, it was found that 55 people had seen movie X, 45 people had seen movie Y, 50 people had seen movie Z, 10 people had not seen any of the movies and 20 people had seen all the three movies (X, Y and Z). How many people had seen only two of the movies?
Explanation
{Total} = {Movie X} + {Movie Y} + {Movie Z} - {Exactly 2 movies} - 2 × {All 3 movies} + {No movies}
Let 'n' denote the number of people who had seen only two of the movies.
Therefore,
100 = 55 + 45 + 50 - n - (2 × 20) + 10
Or, n = 20
Thus, number of people who had seen only two of the movies is 20.
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
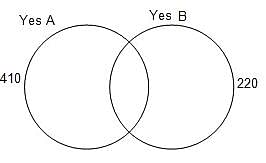
Try yourself:In a survey, 500 people were asked two questions. They were simply to answer 'yes' or 'no'. Of these, 410 people said yes to the first question and 220 people said yes to the second. What is the least number that said yes to both?
Explanation

n(A ∩ B) = n(A) + n(B) - n(A ∪ B)
= 410 + 220 - n(A ∪ B)
To minimise intersection, we need to maximise union, which could be most 500. Putting the value,
We get n(A ∩ B) = 410 + 220 - 500 = 130
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
Try yourself:Every student of a certain school must take one and only one elective course. Last year, 1/2 of the students took biology as an elective subject, 1/3 of the students took chemistry, and the rest took physics. This year, 1/3 of the students who took biology and 1/4 of the students who took chemistry left school. No other student left and no fresh student was admitted. What fraction of all students took biology and chemistry?
Explanation
If total = 1, then:
Last year
B = 1/2
C = 1/3
P = 1/6
This year
B = (1/2) x (2/3) = 1/3
C = (1/3) x (3/4) = 1/4
Total = (1/3) + (1/4) = 7/12
Students left this year:
B = (1/2) x (1/3) = (1/6)
C = (1/3) x (1/4) = (1/12)
Total = (1/6 + 1/12) = (1/4)
Students at the school this year
= Number of students last year - Number of students left this year
= 1 - (1/4)
= (3/4)
Fraction of all students who took biology and chemistry = (7/12) ÷ (3/4) = 7/9
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
Try yourself:In a survey on political preference, 78% of those asked were in favour of at least one of the proposals I, II and III. 50% of those asked favoured proposal I, 30% of them favoured proposal II, and 20% of them favoured proposal III. If 5% of them favoured all three proposals, then what percentage of those asked favoured more than one of the three proposals?
Explanation

Let the total number of people surveyed be 100.
Number of people in favour of at least one proposal = 78
From Venn diagram:
Number of people in favour of exactly two proposals = x + y + z
Number of people in favour of all three proposals = 5
Number of people in favour of only proposal I = 50 - (x + y + 5)
Number of people in favour of only proposal II = 30 - (y + z + 5)
Number of people in favour of only proposal III = 20 - (x + z + 5)
According to the question:
78 = 50 - (x + y + 5) + 30 - (y + z + 5) + 20 - (x + z + 5) + (x + y + z) + (5)
⇒ 78 = 100 - (x + y + z) - 10
⇒ (x + y + z) = 12
Number of people who favoured more than one proposal = Number of people in favour of exactly two proposals +
Number of people in favour of all three proposals
= x + y + z + 5
= 12 + 5 = 17
Required percentage = 17%
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
Try yourself:If X = {8n - 7n - 1 : n ∈ N} and Y = {49(n - 1) : n ∈ N}, then
Explanation
We have: 8n - 7n - 1 = (7 + 1)n - 7n - 1 = (nC2 72 + nC3 73 + … nCn 7n)
= 49(nC2 + nC3 7 + … + nCn 7n - 2) for n ≥ 2. For n = 1, 8n - 7n - 1 = 0.
Thus, 8n - 7n - 1 is a multiple of 49 for n ≥ 2 and 0 for n = 1.
Hence, X consists of all positive integral multiples of 49 of the form 49 Kn, where Kn = nC2 + nC3 7 + … + nCn 7n - 2 together with zero.
Also, Y consists of all positive integral multiple of 49, including zero. Therefore, X ⊂ Y.
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
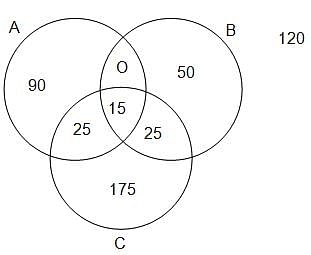
Try yourself:Directions: Study the given information and answer the following question.
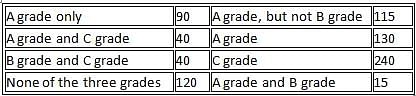
In a survey of 500 customers, the numbers of customers who buy different grades of rice are given below:

Calculate the approximate percentage of customers who buy all three grades of rice.
Explanation

The Venn diagram for the same is as shown.
Percentage of consumers who buy all the 3 grades

Report a problem
Question for Practice Questions Level 2: Set Theory - 2
Try yourself:Directions: Study the given information and answer the following question.
In a survey of 500 customers, the numbers of customers who buy different grades of rice are given below:

The number of customers who buy A or B, but not C, is
Explanation

Number of customers who buy A or B, but not C = 90 + 50 + 0 = 140
Report a problem
Question for Practice Questions Level 2: Set Theory - 2
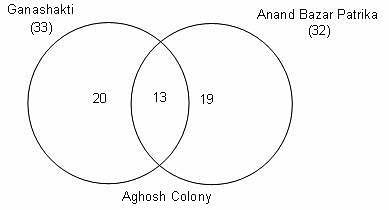
Try yourself:Directions: Read the given information and answer the following question.
Ghosh Babu is staying at Ghosh Housing Society, Aghosh Colony, Dighoshpur, Kolkata. In Ghosh Housing Society, 6 persons daily read Ganashakti and 4 persons read Anand Bazar Patrika. In this society, there is no person who reads both the newspapers. The total numbers of persons who read these two newspapers in Aghosh Colony and in Dighoshpur are 52 and 200, respectively. The numbers of persons who read Ganashakti in Aghosh Colony and in Dighoshpur are 33 and 121, respectively, while the numbers of persons who read Anand Bazar Patrika in Aghosh Colony and in Dighoshpur are 32 and 117, respectively.
Q. The number of persons in Dighoshpur who read only Ganashakti is
Explanation
Report a problem