Hybridization & Shapes Of Molecules | Inorganic Chemistry PDF Download
SHAPES AND HYBRIDISATION OF MOLECULES
1. S.N. = 2
Hybridisation = sp; Orbitals participating = s + px (py or pz);
Geometry = linear; Shape = linear
Examples: BeCl2 , BeF2, NO2+, C2H2, CO2 [Ag(NH3)2]+
2. S.N. = 3
Hybridisation = sp2;
Orbitals participating = s + px + py
Geometry = trigonal planar
Case - 1: 3 bond pair; Shape = planar
Examples: BCl3, BeF3–, BO33–, SO3, NO3–, CO32–
Case - 2: 1 lone pair + 2 lone pair, Shape = v-shape
Examples: NO2–, SO2, ClO2+
3. S.N. = 4
(I) Hybridisation = sp3; Orbitals participating = s + px + py + pz
Geometry = tetrahedral
Case - 1: 4 bond pair; Shape = tetrahedral
Examples: CCl4, CH4, PCl4+, SiCl4, ClO4–, [PI4]+, NH4+, BeH42–, BF4–, AlBr4–, SbF4+, SO42– NH3, XeO4, PO43–
Case - 2: 3 bond pair + 1 lone pair; Shape = pyramidal
Examples: NH3, H3O+, PBr2, IO3–, SiF3+, Te(Ne)3+, ClO3–, SnCl3–
Case - 3: 2 bond pair + 2 lone pair; Shape = angular
Examples: H2O, [BrF2]+, [ICl2]+, I3+, [I(CN)2]3+, Cl2O, H2S, SCl2, NH2–, ClF2+, IBr2+, ClO2–
(II) Hybridisation = sd3 Orbitals participating: s + dxy + dyz + dzx
Geometry = Tetrahedral Shape = tetrahedral
Examples: MnO4–, Cr2O72–, CrO42–
(III) Hybridisation = dsp2 [on sp2d for Cu(NH3)4]2+
Orbital Participating = s + px + py + dx2-y2
Geometry = Square planar Shape = Square Planar
Examples: [Ni(CN)4]2-
4. S.N. = 5
(I) Hybridisation = dsp3; Orbitals participating = s + px + pz + py + dz2
Geometry = Trigonal bipyramidal
Case - 1: 5 bond pairs Shape = trigonal bipyramidal
Examples: PCl5, SbF5, AsF5, XeO3F2, [XeF5]+, IO53–, P(CH3)3F2, P(CH3)3(CF3)2
Case - 2: 4 bond pair + 1 lone pair Shape = Sea-saw
Examples: SF4, IF4+, XeO2F2, [XeO3F]–, [XeF4]2+
Case - 3: 3 bond pair + 2 lone pair Shape = T shape
Examples: IF3, XeF3+, XeOF2, [SF3]–
Case - 4: 2 bond pair + 3 lone pair Shape = Linear
Examples: XeF2, I3–, IBr2–, BrF2–, [SF2]2–
II Hybridisation = dsp3; Orbitals participating = s + px + py + pz + dx2 - y2
Geometry = square pyramidal Shape = Square pyramidal
Examples: [Ni(CN)5]3-
5. S.N. = 6
Hybridisation = sp3d2 Orbitals participating = s+px+py + pz + dz2 + d x2 - y2
Geometry = Octahedral
Case - 1: 6 bond pair Shape = octahedral
Example: SF6, FeF64-, [AlF6]3-, SeF6, [GaCl6]3-, [BiCl6]-, [IF6]+, [PF6]-, [XeO6]4-, [PCl6]-, [IO6]5-
Case - 2: 5 bond pair + 1 lone pairShape = square pyramidal
Example: SbF52–, XeF5–, TeCl5–, BrF5, IF5, XeOF4, BrOF4–
Case - 3: 4 bond pair + 2 lone pair Shape = square planar
Examples: XeF4, I5–, ICl4–, BrF4–
6. S.N. = 7
Hybridisation = sp3d3 Orbitals participating = s+px+py+ pz+ d x 2 - y2 + dz2 +dxy
Geometry = pentagonal bipyramidal
Case - 1: 7 bond pair Shape = pentagonal bipyramidal
Examples: IF7, FeF7
Case - 2: 6 bond pair + 1 lone pair Shape = distorted octahedral
Examples: XeF6, FeCl62-, IF6-, [XeOF5]-, I7-
7. S.N. = 8
Hybridisation = sp3d4
Examples: [XeF7]–, I82–
(I) Orbitals participating = s + px + py + pz + dxy + dyz + dzx + d x 2 - y2
Shape = Antiprismatic
(II) Orbitals participating = s + px + py + pz + dxy + dyz + dzx + dz2
Shape = Dodecahydral
8. S.N. = 9
Hybridisation = p3d5
Example: [XeF8]2–
Illustration: What is the shape of XeO3?
Solution: XeO3 has 3 bond pair and 1 lone pair. Thus steric no. = 4 Hybridisation becomes sp3, geometry is tetrahedral but because of 1 lone pair shape becomes pyramidal.
Illustration: What is the shape of BrCl3?
Solution: XeO3 has 3 bond pair and 2 lone pair. Thus steric no. = 5 Hybridisation becomes dsp3, geometry is trigonal bipyramidal but because of 2 lone pair shape becomes T-shape
MOLECULAR ORBITALTHEORY
As in the case of atomic orbitals, Schrodinger equations can be written for electrons in molecules. Approximate solutions to these molecular Schrodinger equations can be constructed from linear combinations of the atomic orbitals (LCAO), the sums and differences of the atomic wave functions.
For diatomic molecules such as H2, such wave functions have the form where ψ is the molecular wave function, ψa and ψb are atomic wave functions, and ca and cb are adjustable coefficients. The coefficients can be equal or unequal, positive or negative, depending on the individual orbitals and their energies.
As the distance between two atoms is decreased, their orbitals overlap, with significant probability for electrons from both atoms in the region of overlap. As a result, molecular orbitals form. Electrons in bonding molecular orbitals occupy the space between the nuclei, and the electrostatic forces between the electrons and the two positive nuclei hold the atoms together.
Fig. (a) ψA and ψB for individual hydrogen atoms
(b) ψb = ψA + ψB.
(c) Probability function for the bonding orbital, ψa2
(d) ψa = ψA - ψB.
(e) Probability function for the antibonding orbital, ψa2.
Molecular Orbitals From s-Orbitals: Consider first the combination of two s orbitals, as in H2. For convenience, we label the atoms of a diatomic molecule a and b, so the atomic orbital wave functions are ψ(1sa) and ψ(1sb).
We can visualize the two atoms moving closer to each other until the electron clouds overlap and merge into larger molecular electron clouds. The resulting molecular orbitals are linear combinations of the atomic orbitals, the sum of the two orbitals and the difference between them. 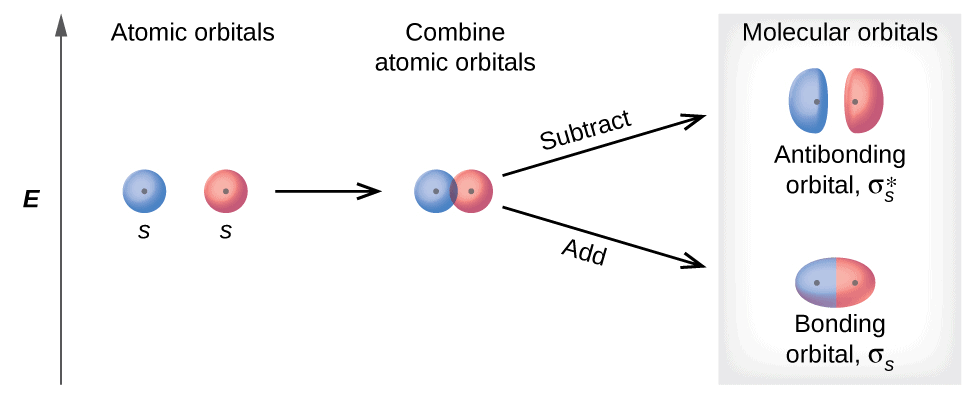 Formation of molecular orbitals
Formation of molecular orbitals
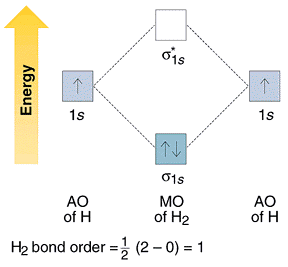 Energy level diagram
Energy level diagram
σ molecular orbital is the sum of the two atomic orbitals and results in the increased concentration of electrons between the two nuclei where both atomic wave functions contribute, it is a bonding molecular orbital and has a lower energy than the starting atomic orbitals. The σ* molecular orbital is the difference of the two atomic orbitals.
It has a node with zero electron density between the nuclei caused by cancellation of the two wave functions and has a higher energy; it is therefore called an antibonding orbital. Electrons in bonding orbitals are concentrated between the nuclei and attract the nuclei and hold them together. Antibonding orbitals have one or more nodes between the nuclei; electrons in these orbitals and the initial atomic orbitals is slightly larger than the same difference between a bonding orbitals and the initial atomic orbitals.
Non-bonding orbitals are also possible. The energy of a nonbonding orbitals is essentially that of an atomic orbital, either because the orbital on one atom has a symmetry that does not match any orbitals on the other atom, or the energy of the molecular orbital matches that of the atomic orbital by coincidence.
Molecular Orbitals from p-Orbitals: The algebraic sign of the wave function must be included when interactions between the orbitals are considered. When two orbitals overlap and the overlapping regions have the same sign, the sum of the two orbitals has an increased electron probability in the overlap region.
When two regions of opposite sign overlap, the combination has a decreased electron probability in the overlap region. For convenience, we will choose a common z-axis connecting the nuclei. pz orbitals subtract to form s and add to form σ* orbitals, both of which are symmetric to rotation about the z axis and with nodes perpendicular to the line that connects the nuclei. Interactions between px and py orbitals lead to π and π* orbitals
Molecular Orbitals From d-Orbitals: When the z-axis are collinear, two dz2 orbitals can combine end on for s bonding. The dxz and dyz orbitals form p orbitals. When atomic orbital meet from two parallel planes and combine side to side, as do the dx2-y2 and dxy orbitals with collinear z axis, they form δ (delta) orbitals.
Nonbonding Orbitals and Other Factors: There can also be nonbonding molecular orbitals, whose energy is essential that of the original atomic orbitals. These can form when there are three atomic orbitals of the same symmetry and similar energies, a situation that requires the formation of three molecular orbitals. One is a low-energy bonding orbital, one is a high-energy antibonding orbital, and one is of intermediate energy and is a nonbonding orbital.
Sometimes, atomic orbitals whose symmetries do not match and therefore remain unchanged in the molecule are also called nonbonding. For example, the s and dyz orbitals of the preceding example are nonbonding with respect to each other.
|
50 videos|92 docs|41 tests
|
FAQs on Hybridization & Shapes Of Molecules - Inorganic Chemistry
| 1. What is hybridization and how does it relate to the shapes of molecules? |  |
| 2. How does hybridization affect the bond angles in a molecule? |  |
| 3. Can you provide an example of hybridization and its impact on molecular shape? |  |
| 4. How does the concept of hybridization explain the shape of molecules with double or triple bonds? |  |
| 5. How does hybridization affect the overall polarity of a molecule? |  |

















